反ド・ジッター空間

3次元反ド・ジッター空間は、双曲面円盤の積み重ねのようなもので、それぞれの円盤は特定の時点における宇宙の状態を表しています。^{[ a ]}

数学と物理学において、n次元反ド・ジッター空間（AdS _n）は、一定の負のスカラー曲率を持つ最大対称ローレンツ多様体である。反ド・ジッター空間とド・ジッター空間は、ライデン大学の天文学教授でライデン天文台の所長であったウィレム・ド・ジッター（1872年5月6日 - 1934年11月20日）にちなんで名付けられた。ウィレム・ド・ジッターとアルバート・アインシュタインは1920年代にライデンで宇宙の時空構造について緊密に協力した。ポール・ディラックは1963年に反ド・ジッター空間を厳密に探究した最初の人物である。^{[ 1 ] [ 2 ] [ 3 ] [ 4 ]}

一定曲率の多様体は2 次元の場合に最もよく知られており、楕円平面または球面は一定の正の曲率の表面であり、平面 (つまりユークリッド) は一定のゼロ曲率の表面であり、双曲面は一定の負の曲率の表面です。

アインシュタインの一般相対性理論は、空間と時間を同等の立場に置くため、空間と時間を別々に考えるのではなく、統一された時空の幾何学を考える。定曲率時空の例としては、ド・ジッター空間（正）、ミンコフスキー空間（零）、反ド・ジッター空間（負）が挙げられる。したがって、これらはそれぞれ、正、零、負の宇宙定数を持つ空の宇宙に対するアインシュタイン場の方程式の厳密解である。

反ド・ジッター空間は、任意の次元数に一般化されます。高次元においては、AdS/CFT対応における役割で最もよく知られています。AdS/CFT対応は、量子力学における力（電磁気力、弱い力、強い力など）を、弦理論を用いて、ある次元数（例えば4次元）において記述できることを示唆しています。弦理論では、弦は反ド・ジッター空間に存在し、さらに1つの（非コンパクト）次元が追加されます。

非技術的な説明

技術用語の翻訳

最大対称性を持つローレンツ多様体とは、空間と時間のどの点も他の点と区別できない時空であり、（ローレンツ多様体であるため）時空点における方向（または経路の接線）を区別できる唯一の方法は、それが空間的、光的、または時間的であるかどうかである。特殊相対論の空間（ミンコフスキー空間）がその一例である。

一定のスカラー曲率とは、物質やエネルギーが存在しない場合に時空のどこでも同じ単一の数値で記述される曲率を持つ、一般相対性理論の重力のような時空の曲がりを意味します。

負の曲率は、鞍型の表面やトランペットのベルに似たガブリエルの角の表面のように、双曲的に曲がっていることを意味します。

一般相対性理論における時空

一般相対性理論は、時間、空間、重力の性質に関する理論であり、重力とは物質またはエネルギーの存在によって生じる空間と時間の曲率です。エネルギーと質量は等価です（式E  =  mc ²で表されるように）。空間と時間の値は、光速を乗じたり除したりすることで、それぞれ時間と空間の単位に関連付けられます（例：秒×メートル/秒はメートル）。

よくある例え話として、重い物体を乗せた平らなゴム板がへこむと、近くを転がる小さな物体の軌道が影響を受け、重い物体がなかった場合にたどっていたであろう軌道から内側に逸れてしまうというものがあります。もちろん、一般相対性理論では、小さな物体と大きな物体の両方が時空の曲率に相互に影響を与えます。

物質によって作り出される重力の引力は、時空の負の曲率によるもので、ゴムシートの例えでは、シートが負に曲がっている（トランペットのベルのような）凹みで表されます。

一般相対性理論の重要な特徴は、重力を電磁力のような従来の力としてではなく、物質またはエネルギーの存在によって生じる時空の幾何学的形状の変化として記述することです。

上記のアナロジーは、一般相対性理論における重力によって生じる二次元空間の曲率を、三次元超空間において記述するものであり、三次元超空間では三次元目が重力の影響に対応する。一般相対性理論を幾何学的に考察すると、現実世界の四次元空間における重力の影響は、その空間を五次元超空間に投影することで幾何学的に記述される。五次元目は、一般相対性理論における重力および重力に類似した影響によって生じる時空の曲率に対応する。

その結果、一般相対性理論において、おなじみのニュートン力の方程式 （すなわち、2つの物体間の引力は、重力定数にそれらの質量の積をそれらの間の距離の2乗で割った値に等しい）は、一般相対性理論で見られる重力効果の単なる近似値に過ぎません。しかし、この近似値は、相対論的な速度（特に光）や非常に大きく高密度な質量など、極端な物理的状況では不正確になります。 ${\displaystyle \textstyle F=G{\frac {m_{1}m_{2}}{r^{2}}}\ }$

一般相対性理論では、重力は時空が曲がっている（「歪んでいる」）ことによって生じます。重力を曲がった空間に帰するのはよくある誤解です。相対性理論では、空間も時間も絶対的な意味を持ちません。しかしながら、地球上のように弱い重力を記述するには、特定の座標系における時間の歪みを考慮すれば十分です。地球上の重力は非常に顕著ですが、相対論的な時間の歪みを検出するには精密な機器が必要です。私たちが日常生活で相対論的効果に気づかないのは、光速（c =）が非常に大きいためです。宇宙の速度はおよそ300,000  km/sであり、これによって私たちは空間と時間を別のものとして認識することになります。

一般相対論におけるド・ジッター空間

ド・ジッター空間は、物質やエネルギーが存在しない状態で時空（dS空間）が正に曲がっているという一般相対性理論の解である。これはユークリッド幾何学と非ユークリッド幾何学の関係に類似している。

物質やエネルギーが存在しない時空の固有曲率は、一般相対論における宇宙定数によってモデル化される。これは、真空がエネルギー密度と圧力を持つことに対応する。この時空幾何学は、瞬間的に平行な時間的測地線^{[ b ]}が発散し、空間的断面は正の曲率を持つという結果をもたらす。

反ド・ジッター空間とド・ジッター空間の区別

一般相対性理論における反ド・ジッター空間は、時空の曲率の符号が異なる点を除けば、ド・ジッター空間に類似している。反ド・ジッター空間では、物質やエネルギーが存在しない状態で、空間的断面の曲率は負であり、双曲幾何学に対応し、瞬間的に平行な時間的測地線^{[ b ]}は最終的に交差する。これは負の宇宙定数に対応し、空の空間自体は負のエネルギー密度を持ちながら正の圧力を持つ。これは、我々の宇宙の標準的なΛCDM モデルとは異なり、遠方の超新星の観測から正の宇宙定数が示され、（将来的には漸近的に）ド・ジッター空間に対応する。

反ド・ジッター空間では、ド・ジッター空間と同様に、固有の時空曲率は宇宙定数に対応します。

反ド・ジッター空間AdS ₂は、時間的ラベルと空間的ラベルの交換によってド・ジッター空間dS _{2でもある。} ^{[ 5 ]}このような再ラベル付けは、慣例的に空間的ラベルが付けられた方向を参照する曲率の符号を反転する。

5次元に埋め込まれたド・ジッター空間と反ド・ジッター空間

上記のアナロジーは、1次元上の平坦な周囲空間における重力によって引き起こされる2次元空間の曲率を説明しています。同様に、4次元の（曲がった）ド・ジッター空間と反ド・ジッター空間はそれぞれ、5次元の（平坦な）擬リーマン空間に埋め込むことができます。これにより、埋め込まれた空間内の距離と角度は、5次元の平坦な空間内の距離と角度から直接決定できます。

注意点

この記事の残りの部分では、これらの概念の詳細を、より厳密かつ正確な数学的・物理的な記述を用いて説明します。人間は5次元以上のものを視覚化することに不向きですが、数式はそのような問題を抱えることはありません。数式は、視覚化しやすい3次元や4次元の概念を記述するのと同様に、5次元の概念を適切に表現することができます。

より正確な数学的記述には、上記の類推に基づく発見的記述とは異なる、特に重要な含意があります。反ド・ジッター空間の数学的記述は、曲率の概念を一般化します。この数学的記述において、曲率は特定の点の特性であり、時空内の曲がった点が融合する目に見えない面から切り離すことができます。例えば、特異点（一般相対性理論で最もよく知られているのはブラックホール）のような概念は、現実世界の幾何学では完全に表現できませんが、数式の特定の状態に対応することができます。

完全な数学的記述は、一般相対性理論における空間的次元と時間的次元の間の微妙な違いも捉えています。

定義と特性

球面空間と双曲空間が、1次元高い平坦空間（それぞれ球面と擬球面）への等長埋め込みによって視覚化できるのと同様に、反ド・ジッター空間は、球面を1次元追加した空間に埋め込むローレンツ的類似体として視覚化できる。この場合、追加次元は第二の時間的次元である。本稿では、時間的方向の計量テンソルは負であるという慣例を採用する。

平坦な(1 + 2 )次元空間に埋め込まれた(1 + 1)次元反ド・ジッター空間のイメージ。t 1_軸とt ₂軸は回転対称面上にあり、x _{1軸はその面に対して垂直である。埋め込まれた面には、} x ₁軸を取り囲む閉じた時間的曲線が含まれる。

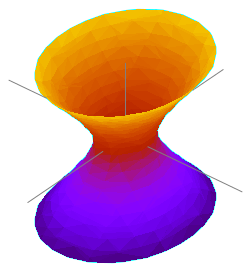
署名( p , 1)の反ド・ジッター空間は、座標( x ₁ , ..., x _p , t ₁ , t ₂ )の空間に等長的に埋め込まれ、計量${\displaystyle \mathbb {R} ^{p,2}}$

${\displaystyle ds^{2}=\sum _{i=1}^{p}dx_{i}^{2}-dt_{1}^{2}-dt_{2}^{2}}$

準球として

${\displaystyle \sum _{i=1}^{p}x_{i}^{2}-t_{1}^{2}-t_{2}^{2}=-\alpha ^{2},}$

ここで、αは長さ（曲率半径）の次元を持つ非ゼロの定数です。埋め込み内の各点は、原点から一定の「距離」（二次形式によって決定されます）を持ちますが、図に示すように 双曲面として表すことができます。

反ド・ジッター空間上の計量は、アンビエント計量から誘導される計量である。これは非退化であり、ローレンツ符号を持つ。

閉じた時間的曲線と普遍被覆

上記の埋め込みには、閉じた時間的曲線があります。たとえば、t ₁ = α sin( τ )、t ₂ = α cos( τ ) 、および他のすべての座標が 0 でパラメータ化されたパスは、そのような曲線です。このような曲線は、普遍被覆空間に渡して、埋め込みを効果的に「展開」することで削除できます。同様の状況が擬球でも発生します。擬球は、双曲平面とは異なり、自身に巻き付きます。その結果、双曲平面にはない自己交差直線（測地線）が含まれます。一部の著者は、反ド・ジッター空間を埋め込まれた準球自体と同等と定義し、他の著者はそれを埋め込みの普遍被覆と同等と定義しています。

対称性

普遍被覆が取られていない場合、( p , 1)反ド・シッター空間はO( p , 2)をその等長群として持ちます。普遍被覆が取られている場合、等長群はO( p , 2)の被覆です。これは、以下に示す商空間構成を用いて、反ド・シッター空間を対称空間として定義することで最も簡単に理解できます。

不安定

物理学者ピオトル・ビゾンとアンジェイ・ロストウォロウスキが2011年に提唱した未証明の「AdS不安定性予想」は、AdSにおける特定の形状の任意の小さな摂動がブラックホールの形成につながるというものである。^{[ 6 ]}数学者ゲオルギオス・モシディスは、球対称性を前提とすれば、内部ミラーを持つアインシュタインゼロダストシステム（2017年）とアインシュタイン質量ゼロのヴラソフシステム（2018年）という特定のケースにおいてこの予想が成り立つことを証明した。^{[ 7 ] [ 8 ]}

座標パッチ

空間の一部を覆う座標パッチは反ド・ジッター空間の半空間座標化を与え、これは双曲空間のポアンカレ半平面モデルに似ているが、計量の項の1つが否定され、半空間の境界の接線方向の1つに対応する。このパッチの 計量は

${\displaystyle ds^{2}={\frac {1}{y^{2}}}\left(-dt^{2}+dy^{2}+\sum _{i}dx_{i}^{2}\right),}$

半空間を与える。この計量は平坦な半空間ミンコフスキー時空と 共形的に同値である。${\displaystyle y>0}$

この座標パッチの定数時間スライスは、ポアンカレ半空間計量における双曲的空間である。 の極限において、この半空間計量はミンコフスキー計量 と共形的に同値である。したがって、反ド・ジッター空間は無限遠において共形ミンコフスキー空間を含む（このパッチでは「無限遠」はy座標が0である）。 ${\displaystyle y\to 0}$ ${\textstyle ds^{2}=-dt^{2}+\sum _{i}dx_{i}^{2}}$

AdSでは時空は周期的であり、普遍被覆は非周期的な時間を持つ。上の座標パッチは時空の1周期の半分を覆っている。

AdS の共形無限大は時間的であるため、共形無限大に関連付けられた境界条件がない限り、空間的超曲面上の初期データを指定しても、将来の進化を一意に（つまり決定論的に）決定することはできません。

反ド・ジッター空間の「半空間」領域とその境界

隣の画像は、反ド・ジッター空間の「半空間」領域とその境界を表しています。円筒の内部は反ド・ジッター時空に対応し、円筒の境界は共形境界に対応しています。内部の緑色の陰影部分は、半空間座標で覆われたAdS領域に対応し、2つのヌル（光のような）測地線超平面によって囲まれています。表面の緑色の陰影部分は、ミンコフスキー空間で覆われた共形空間領域に対応しています。

緑色の網掛け領域は AdS 空間の半分と共形時空の半分をカバーします。緑色の円盤の左端は右端と同じように接触します。

均質対称空間として

2次元球面の場合と同様に

${\displaystyle S^{2}={\mathrm {O} (3)}/{\mathrm {O} (2)}}$

は2つの直交群の商であり、パリティ（反射対称性）と時間反転対称性を持つ反ド・ジッター空間は2つの一般化直交群の商として見ることができる。

${\displaystyle \mathrm {AdS} _{n}={\mathrm {O} (2,n-1)}/{\mathrm {O} (1,n-1)}}$

一方、PやCを除いたAdSは商として見ることができる。

${\displaystyle {\mathrm {スピン} ^{+}(2,n-1)}/{\mathrm {スピン} ^{+}(1,n-1)}}$

スピングループの。

この商の定式化は同次空間の構造を与える。一般化直交群のリー代数は行列で与えられる。 ${\displaystyle \mathrm {AdS} _{n}}$ ${\displaystyle {\mathcal {o}}(1,n)}$

${\displaystyle {\mathcal {H}}={\begin{pmatrix}{\begin{matrix}0&0\\0&0\end{matrix}}&{\begin{pmatrix}\cdots 0\cdots \\\leftarrow v^{\text{t}}\rightarrow \end{pmatrix}}\\{\begin{pmatrix}\vdots &\uparrow \\0&v\\\vdots &\downarrow \end{pmatrix}}&B\end{pmatrix}}}$ 、

ここでは歪対称行列である。 のリー代数における相補生成元は ${\displaystyle B}$ ${\displaystyle {\mathcal {G}}={\mathcal {o}}(2,n)}$

${\displaystyle {\mathcal {Q}}={\begin{pmatrix}{\begin{matrix}0&a\\-a&0\end{matrix}}&{\begin{pmatrix}\leftarrow w^{\text{t}}\rightarrow \\\cdots 0\cdots \\\end{pmatrix}}\\{\begin{pmatrix}\uparrow &\vdots \\w&0\\\downarrow &\vdots \end{pmatrix}}&0\end{pmatrix}}.}$

これら2つは を満たします。明示的な行列計算により および であることが示されます。したがって、反ド・ジッター空間は、簡約同次空間であり、非リーマン対称空間です。 ${\displaystyle {\mathcal {G}}={\mathcal {H}}\oplus {\mathcal {Q}}}$ ${\displaystyle [{\mathcal {H}},{\mathcal {Q}}]\subseteq {\mathcal {Q}}}$ ${\displaystyle [{\mathcal {Q}},{\mathcal {Q}}]\subseteq {\mathcal {H}}}$

物理学におけるAdS時空とその特性の概要

${\displaystyle \mathrm {AdS} _{n}}$ は、負の宇宙定数（ ）を持つアインシュタイン・ヒルベルト作用を伴う重力理論のn次元真空解であり、次のラグランジアン密度 で記述される理論である。${\displaystyle \Lambda }$ ${\displaystyle \Lambda <0}$

${\displaystyle {\mathcal {L}}={\frac {1}{16\pi G_{(n)}}}(R-2\Lambda )}$ 、

ここで、 G _{( n )は}n次元時空における重力定数である。したがって、これはアインシュタイン場の方程式の解である。

${\displaystyle G_{\mu \nu }+\Lambda g_{\mu \nu }=0,}$

ここではアインシュタインテンソル、 は時空の計量である。半径を と導入すると、この解は、 次の制約により 、計量が座標にある-次元平坦時空に浸漬することができる。${\displaystyle G_{\mu \nu }}$ ${\displaystyle g_{\mu \nu }}$ ${\displaystyle \alpha }$ ${\textstyle \Lambda ={\frac {-1}{\alpha ^{2}}}{\frac {(n-1)(n-2)}{2}}}$ ${\displaystyle (n+1)}$ ${\displaystyle \mathrm {diag} (-1,-1,+1,\ldots ,+1)}$ ${\displaystyle (X_{1},X_{2},X_{3},\ldots ,X_{n+1})}$

${\displaystyle -X_{1}^{2}-X_{2}^{2}+\sum _{i=3}^{n+1}X_{i}^{2}=-\alpha ^{2}.}$

グローバル座標

${\displaystyle \mathrm {AdS} _{n}}$ 次のようにパラメータによってグローバル座標でパラメータ化されます。 ${\displaystyle (\tau ,\rho ,\theta ,\varphi _{1},\ldots ,\varphi _{n-3})}$

${\displaystyle {\begin{cases}X_{1}=\alpha \cosh \rho \cos \tau \\X_{2}=\alpha \cosh \rho \sin \tau \\X_{i}=\alpha \sinh \rho \,{\hat {x}}_{i}\qquad \sum _{i}{\hat {x}}_{i}^{2}=1\end{cases}}}$ 、

ここで球面を媒介変数化し、座標系では、、などとなる。これらの座標系における計量は以下の通りである。 ${\displaystyle {\hat {x}}_{i}}$ ${\displaystyle S^{n-2}}$ ${\displaystyle \varphi _{i}}$ ${\displaystyle {\hat {x}}_{1}=\sin \theta \sin \varphi _{1}\ldots \sin \varphi _{n-3}}$ ${\displaystyle {\hat {x}}_{2}=\sin \theta \sin \varphi _{1}\ldots \cos \varphi _{n-3}}$ ${\displaystyle {\hat {x}}_{3}=\sin \theta \sin \varphi _{1}\ldots \cos \varphi _{n-2}}$ ${\displaystyle \mathrm {AdS} _{n}}$

${\displaystyle ds^{2}=\alpha ^{2}\left(-\cosh ^{2}\rho \,d\tau ^{2}+\,d\rho ^{2}+\sinh ^{2}\rho \,d\Omega _{n-2}^{2}\right)}$

ここで、およびである。時間の周期性と閉じた時間的曲線（CTC）を避けるためには、普遍被覆 をとるべきである。極限において、この時空の境界、通常共形境界と呼ばれる境界に近づくことができる。 ${\displaystyle \tau \in [0,2\pi ]}$ ${\displaystyle \rho \in \mathbb {R} ^{+}}$ ${\displaystyle \tau }$ ${\displaystyle \tau \in \mathbb {R} }$ ${\displaystyle \rho \to \infty }$ ${\displaystyle \mathrm {AdS} _{n}}$

変換とを使用すると、グローバル座標で 通常のメトリックを取得できます。${\displaystyle r\equiv \alpha \sinh \rho }$ ${\displaystyle t\equiv \alpha \tau }$ ${\displaystyle \mathrm {AdS} _{n}}$

${\displaystyle ds^{2}=-f(r)\,dt^{2}+{\frac {1}{f(r)}}\,dr^{2}+r^{2}\,d\Omega _{n-2}^{2}}$

どこ${\displaystyle f(r)=1+{\frac {r^{2}}{\alpha ^{2}}}}$

双曲面モデル + 時間座標

「定義と特性」の項でAdS空間の定式化を採用し、座標とを極座標に変換すると、ラジアル座標は、および角座標は、および、空間が周期で周期である周期であるとき、準球は ${\displaystyle t_{1}}$ ${\displaystyle t_{2}}$ ${\displaystyle x_{0}}$ ${\displaystyle \varphi }$ ${\displaystyle t_{1}=x_{0}\cos \varphi }$ ${\displaystyle t_{2}=x_{0}\sin \varphi }$ ${\displaystyle \varphi }$ ${\displaystyle 2\pi }$

${\displaystyle \sum _{i=1}^{p}x_{i}^{2}-x_{0}^{2}=-\alpha ^{2},}$

そしてその指標は

${\displaystyle ds^{2}=\sum _{i=1}^{p}dx_{i}^{2}-dx_{0}^{2}-(x_{0}d\varphi )^{2}.}$

準球面はp次元双曲面空間の双曲面モデルにおける多様体と同じ方程式を取り、計量も双曲面モデルにおける計量の方程式を取りますが、追加の項は除きます。これは、準球面が方向に並進対称であること、そして が固定された の準球面上の曲線は空間的であるのに対し、準球面自身は時間的であり、他のすべての座標が固定されている場合、 が大きくなるにつれて固有時間がより速く発展することを示しています。つまり、 ${\displaystyle -(x_{0}d\varphi )^{2}}$ ${\displaystyle \varphi }$ ${\displaystyle \varphi }$ ${\displaystyle \varphi }$ ${\displaystyle \tau }$ ${\displaystyle x_{0}}$ ${\displaystyle \varphi }$

${\displaystyle \left.{\frac {d\tau }{d\varphi }}\right|_{x_{0},x_{1},\dots ,x_{p}}=x_{0}.}$

をおよびの関数として書くと、分岐点はにあることがわかります。しかし、準球面によって課される制約により となるため、分岐点は準球面の外側に存在し、したがって、グローバル座標の場合と同様に、 において空間が周期的であるという要件を削除することによって空間をその普遍被覆に展開し、そのようにして閉じた時間的曲線(CTC) を回避することができます。 ${\displaystyle \varphi }$ ${\displaystyle t_{1}}$ ${\displaystyle t_{2}}$ ${\displaystyle t_{1}=t_{2}=0}$ ${\displaystyle t_{1}^{2}+t_{2}^{2}\geq 1}$ ${\displaystyle \varphi }$

ポアンカレ座標

次のパラメータ化により:

${\displaystyle {\begin{cases}X_{1}={\frac {\alpha ^{2}}{2r}}\left(1+{\frac {r^{2}}{\alpha ^{4}}}\left(\alpha ^{2}+{\vec {x}}^{2}-t^{2}\right)\right)\\X_{2}={\frac {r}{\alpha }}t\\X_{i}={\frac {r}{\alpha }}x_{i}\qquad i\in \{3,\ldots ,n\}\\X_{n+1}={\frac {\alpha ^{2}}{2r}}\left(1-{\frac {r^{2}}{\alpha ^{4}}}\left(\alpha ^{2}-{\vec {x}}^{2}+t^{2}\right)\right)\end{cases}},}$

ポアンカレ座標における計量は次のとおりです 。${\displaystyle \mathrm {AdS} _{n}}$

${\displaystyle ds^{2}=-{\frac {r^{2}}{\alpha ^{2}}}\,dt^{2}+{\frac {\alpha ^{2}}{r^{2}}}\,dr^{2}+{\frac {r^{2}}{\alpha ^{2}}}\,d{\vec {x}}^{2}}$

ここで である。余次元2の曲面はポアンカレ・キリング・ホライズンであり、時空の境界に近づく。したがって、大域座標とは異なり、ポアンカレ座標は多様体 のすべてを網羅するわけではない。この計量を用いると、次のように書ける。 ${\displaystyle 0\leq r}$ ${\displaystyle r=0}$ ${\displaystyle r\to \infty }$ ${\displaystyle \mathrm {AdS} _{n}}$ ${\displaystyle \mathrm {AdS} _{n}}$ ${\displaystyle u\equiv {\frac {r}{\alpha ^{2}}}}$

${\displaystyle ds^{2}=\alpha ^{2}\left({\frac {\,du^{2}}{u^{2}}}+u^{2}\,dx_{\mu }\,dx^{\mu }\right)}$

ここで。変換により、次のようにも書けます。 ${\displaystyle x^{\mu }=\left(t,{\vec {x}}\right)}$ ${\displaystyle z\equiv {\frac {1}{u}}}$

${\displaystyle ds^{2}={\frac {\alpha ^{2}}{z^{2}}}\left(\,dz^{2}+\,dx_{\mu }\,dx^{\mu }\right).}$

この後者の座標は、 AdS/CFT 対応で通常使用される座標であり、AdS の境界は です。 ${\displaystyle z\to 0}$

FRWオープンスライス座標

AdSは最大対称性を持つため、FRW時空のような空間的に一様かつ等方的な形式にキャストすることも可能となる（フリードマン・ルメートル・ロバートソン・ウォーカー計量を参照）。空間幾何学は負に曲がっている（開いた）ものでなければならず、計量は

${\displaystyle ds^{2}=-dt^{2}+\alpha ^{2}\sin ^{2}(t/\alpha )dH_{n-1}^{2},}$

ここでは次元双曲面上の標準計量である。もちろん、これはAdS​​全体をカバーするものではない。これらの座標は、大域埋め込み座標と次の関係にある。 ${\displaystyle dH_{n-1}^{2}=d\rho ^{2}+\sinh ^{2}\rho d\Omega _{n-2}^{2}}$ ${\displaystyle (n-1)}$

${\displaystyle {\begin{cases}X_{1}=\alpha \cos(t/\alpha )\\X_{2}=\alpha \sin(t/\alpha )\cosh \rho \\X_{i}=\alpha \sin(t/\alpha )\sinh \rho \,{\hat {x}}_{i}\qquad 3\leq i\leq n+1\end{cases}}}$

ここでをパラメータ化します。 ${\displaystyle \sum _{i}{\hat {x}}_{i}^{2}=1}$ ${\displaystyle S^{n-1}}$

デ・シッタースライス

させて

${\displaystyle {\begin{aligned}X_{1}&=\alpha \sinh \left({\frac {\rho }{\alpha }}\right)\sinh \left({\frac {t}{\alpha }}\right)\cosh \xi ,\\X_{2}&=\alpha \cosh \left({\frac {\rho }{\alpha }}\right),\\X_{3}&=\alpha \sinh \left({\frac {\rho }{\alpha }}\right)\cosh \left({\frac {t}{\alpha }}\right),\\X_{i}&=\alpha \sinh \left({\frac {\rho }{\alpha }}\right)\sinh \left({\frac {t}{\alpha }}\right)\sinh \xi \,{\hat {x}}_{i},\qquad 4\leq i\leq n+1\end{aligned}}}$

ここでをパラメータ化します。すると、メトリックは次のようになります。 ${\displaystyle \sum _{i}{\hat {x}}_{i}^{2}=1}$ ${\displaystyle S^{n-3}}$

${\displaystyle ds^{2}=d\rho ^{2}+\sinh ^{2}\left({\frac {\rho }{\alpha }}\right)ds_{dS,\alpha ,n-1}^{2},}$

どこ

${\displaystyle ds_{dS,\alpha ,n-1}^{2}=-dt^{2}+\alpha ^{2}\sinh ^{2}\left({\frac {t}{\alpha }}\right)dH_{n-2}^{2}}$

は、開スライス座標における曲率半径を持つ次元ド・ジッター空間の計量である。双曲計量は次のように与えられる。 ${\displaystyle n-1}$ ${\displaystyle \alpha }$

${\displaystyle dH_{n-2}^{2}=d\xi ^{2}+\sinh ^{2}(\xi )d\Omega _{n-3}^{2}.}$

幾何学的特性

半径nのAdS _n計量は、最大対称性のn次元時空の一つである。以下の幾何学的性質を持つ。 ${\displaystyle \alpha }$

• リーマン曲率テンソル

  ${\displaystyle R_{\mu \nu \alpha \beta }={\frac {-1}{\alpha ^{2}}}(g_{\mu \alpha }g_{\nu \beta }-g_{\mu \beta }g_{\nu \alpha })}$

• リッチ曲率

  ${\displaystyle R_{\mu \nu }={\frac {-1}{\alpha ^{2}}}(n-1)g_{\mu \nu }}$

• スカラー曲率

  ${\displaystyle R={\frac {-1}{\alpha ^{2}}}n(n-1)}$

一般化

曲率がゼロでない最大対称空間族の任意の要素は、座標が（x ₀、...、x _p、y ₁、...、y _q）で計量が次の空間に等長的に埋め込むことができる。${\displaystyle \mathbb {R} ^{p+1,q}}$

${\displaystyle ds^{2}=\sum _{i=0}^{p}dx_{i}^{2}-\sum _{j=1}^{q}dy_{j}^{2}}$

準球として

${\displaystyle \sum _{i=0}^{p}x_{i}^{2}-\sum _{j=1}^{q}y_{j}^{2}=\alpha ^{2},}$

ここで、αは計量次元の長さ（曲率半径）のゼロでない定数です。

計量 はアンビエント計量から誘導される計量であり、シグネチャ( p , q )を持ち、非退化です。

これらの空間には次のようなサブファミリーが識別される可能性があります。

• q = 0 :超球面空間S ^p
• p = 0 : 双曲型空間H ^{q ‍ [c ]}の（二重被覆）
• q = 1 :ド・ジッター空間dS _{p +1}
• p = 1 : 反ド・ジッター空間 AdS _{q +1}

このようにして構築された空間は、等長群としてO( p + 1, q )を持ちます。これは対称空間であり、商空間構築法を用いて構築できます。

注記

1. ここでの時間は、この図において世界線が垂直に走る観測者から見た時間です。図の中央にいるそのような観測者だけが慣性的な観測者です。他のすべての慣性的な観測者は、図の中で世界線が振動しています。
2. つまり、時間のある時点で比較的静止している 2 人の慣性観測者の世界線(それぞれの観測者から見た同時性の空間的セクション)。
3. この定式化では計量は負定値です。

参考文献

1. ディラック、ポール (1963). 「3 + 2 ド・ジッター群の注目すべき表現」 .ジャーナル・オブ・マスマティカル・フィジックス. 4 (7). AIP Publishing: 901– 909. Bibcode : 1963JMP.....4..901D . doi : 10.1063/1.1704016 .
2. Dobrev、Vladimir K. (2016-09-12)、「Case of the Anti-de Sitter Group」、5. Case of the Anti-de Sitter Group、De Gruyter、pp.  162–187、doi : 10.1515/9783110427646-006、ISBN 978-3-11-042764-6、2023年11月1日取得
3. 「nLabにおけるシングルトン表現」 . ncatlab.org . 2023年11月1日閲覧。
4. Mezincescu, Luca; Townsend, Paul K. (2020-01-07). 「IRにおけるDBI」. Journal of Physics A: Mathematical and Theoretical . 53 (4): 044002. arXiv : 1907.06036 . Bibcode : 2020JPhA...53d4002M . doi : 10.1088/1751-8121/ab5eab . ISSN 1751-8121 . 
5. Bengtsson、Ingemar (1998)、Anti-de Sitter space (PDF)、p. 4
6. Bizoń, Piotr; Rostworowski, Andrzej (2011). 「反ド・ジッター時空の弱乱流不安定性」 . Physical Review Letters . 107 (3) 031102. arXiv : 1104.3702 . Bibcode : 2011PhRvL.107c1102B . doi : 10.1103/ PhysRevLett.107.031102 . PMID 21838346. S2CID 31556930 .  
7. 「ブラックホールは、特殊な時空が不安定であることを証明するのに役立つ」 Quanta Magazine、2020年。 2020年5月14日閲覧。
8. Moschidis, Georgios (2018). 「アインシュタイン–質量ゼロのヴラソフ系におけるAdSの不安定性の証明」arXiv : 1812.04268 [ math.AP ].

• Qingming Cheng (2001) [1994]、「反ド・ジッター空間」、数学百科事典、EMS Press
• エリス、GFR；ホーキング、SW（1973）、時空の大規模構造、ケンブリッジ大学出版局、pp.  131-134
• フランシス、C. (2005). 「反ド・ジッター時空の共形境界」. AdS/CFT対応：アインシュタイン計量とその共形境界. IRMA数学・理論物理学講義. 第8巻. チューリッヒ：ヨーロッパ数学会. pp.  205– 216. doi : 10.4171/013-1/8 . ISBN 978-3-03719-013-5。
• 松田 秀 (1984). 「反ド・ジッター空間への上半空間の等長的埋め込みに関する一考察」(PDF) .北海道数学ジャーナル. 13 (2): 123– 132. doi : 10.14492/hokmj/1381757712 .2017年2月4日閲覧。
• ウルフ、ジョセフ・A. (2023). 『定曲率空間』（第6版）. アメリカ数学会. p. 337. ISBN 978-1-4704-7365-5。

外部リンク

• ド・シッター空間と反ド・シッター空間の簡易ガイド– ド・シッター空間と反ド・シッター空間の教育的入門書。本文は簡略化されており、数式はほとんど使用されていません。付録は技術的な内容で、物理学または数学の知識を持つ読者を対象としています。