フィボナッチ数列

数学において、フィボナッチ数列とは、各要素がその前の2つの要素の和となる数列です。フィボナッチ数列を構成する数はフィボナッチ数と呼ばれ、一般的にFn_と^{表記されます。多くの著者は0と1から数列を始めますが、1と1 [ 1 ] [ 2 ]}から始める著者もいれば、フィボナッチのように1と2から始める著者もいます。0と1から数列が始まります

0、1、1、2、3、5、8、13、21、34、55、89、144、…（OEISのシーケンスA000045）

辺の長さがフィボナッチ数列の1、1、2、3、5、8、13、21となる正方形のタイル

フィボナッチ数は紀元前200年頃、ピンガラによる2つの長さの音節からなるサンスクリット詩の可能なパターンを列挙した著作の中で、インドの数学で初めて記述されました。 ^{[ 3 ] [ 4 ] [ 5 ]フィボナッチ数は、1202年に著書}『算盤の書』で西ヨーロッパの数学に数列を紹介したイタリアの数学者レオナルド・ディ・ピサ（フィボナッチとしても知られています）にちなんで名付けられました。^{[ 6 ]}

フィボナッチ数は数学において意外にも頻繁に登場し、その研究に特化した学術誌「フィボナッチ・クォータリー」が刊行されているほどです。フィボナッチ数の応用としては、フィボナッチ探索法やフィボナッチ・ヒープ・データ構造といったコンピュータアルゴリズム、並列システムや分散システムを相互接続するために使用されるフィボナッチ・キューブと呼ばれるグラフなどが挙げられます。また、木の枝分かれ、茎における葉の配置、パイナップルの果実の発芽、アーティチョークの開花、松ぼっくりの苞葉の配置など、生物学的な場面にも見られますが、すべての種に見られるわけではありません。

フィボナッチ数は黄金比とも密接に関連しています。ビネの公式は、n番目のフィボナッチ数をnと黄金比で表し、連続する2つのフィボナッチ数の比はnが増加するにつれて黄金比に近づくことを示しています。フィボナッチ数はルーカス数とも密接な関連があり、ルーカス数も同じ漸化式に従い、フィボナッチ数と相補的なルーカス数列を形成します。

定義

フィボナッチ螺旋：フィボナッチタイルの正方形の対角を結ぶ円弧を描くことで作成される黄金螺旋の近似値（前の画像を参照）

フィボナッチ数は、再帰関係^{[ 7 ]} および n >1 で定義される。 $${\displaystyle F_{0}=0,\quad F_{1}=1,}$$ $${\displaystyle F_{n}=F_{n-1}+F_{n-2}}$$

いくつかの古い定義では値が省略され、シーケンスはから始まり、再帰はn > 2に対して有効です。^{[ 8 ] [ 9 ]}${\displaystyle F_{0}=0}$ ${\displaystyle F_{1}=F_{2}=1,}$ ${\displaystyle F_{n}=F_{n-1}+F_{n-2}}$

最初の 20 個のフィボナッチ数F _nは次のとおりです。

F0	F1	F2​	F3	F4	F5​	F6	F7	F8​	F9	F10	F11​	F12	F13	F14​	F15	F16	F17​	F18	F19
	1	1	2	3	5	8	13	21	34	55	89	144	233	377	610	987	1597	2584	4181

フィボナッチ数列は、負の方向の同じ再帰関係に従うことで、負の整数の添え字に拡張できます（OEISのA039834数列）。n < 0の場合、 ⁠ ⁠、⁠ ⁠、⁠ ⁠となります。フィボナッチ数列のほぼすべての特性は、添え字が正か負かに依存しません。正と負の添え字の値は、次の関係に従います。^{[ 10 ]}${\displaystyle F_{1}=1}$ ${\displaystyle F_{0}=0}$ ${\displaystyle F_{n}=F_{n+2}-F_{n+1}$ $${\displaystyle F_{-n}=(-1)^{n+1}F_{n}.}$$

歴史

インド

長さ6の韻律で長音節と短音節を並べる方法は13通り（F _{7 ）あります。8通り（} F ₆）は短音節で終わり、5通り（F ₅）は長音節で終わります

フィボナッチ数列は、インド数学においてサンスクリット語の韻律と関連して登場する。^{[ 4 ] [ 11 ] [ 12 ]}サンスクリット詩の伝統では、持続時間が2単位の長音節（L）と持続時間が1単位の短音節（S）を並置したすべてのパターンを列挙することに関心があった。与えられた総持続時間を持つ連続するLとSの異なるパターンを数えると、フィボナッチ数列が得られる。持続時間がm単位のパターンの数はF _{m +1}である。^{[ 5 ]}

フィボナッチ数列に関する知識は、ピンガラ（紀元前 450年頃～紀元前200年頃）の時代にはすでに存在していた。シンは、ピンガラの謎めいた公式「ミスラウ・チャ」 （「2つは混ざり合っている」）と、それを文脈から解釈して、 m拍（F _{m +1} ）のパターンの数は、F _mの場合に[S]を1つ、 F _{m −1}の場合に[L]を1つ加えることによって得られると述べている学者を引用している。^{[ 13 ]}バラタ・ムニも、ナティヤ・シャーストラ（紀元前 100年頃～紀元後 350年頃）の中で、この数列に関する知識を述べている。 ^{[ 3 ] [ 4 ]}しかし、この数列に関する最も明確な解説は、ヴィラハンカ​​（紀元後700年頃） の著作に見られる。ヴィラハンカ​​自身の著作は失われているが、ゴーパーラ（紀元後 1135年頃） の引用として入手可能である。 ^{[ 12 ]}

前の2つの拍子の変化[が変化です]...たとえば、長さが4の拍子の場合、2と3の拍子の変化が混在すると、5が発生します。[例8、13、21を計算します]...このプロセスは、すべてのmātrā-vṛttas（韻律の組み合わせ）で従う必要があります。^{[ a ]}

ヘマチャンドラ（ 1150年頃 ）もこの順序を知っていたとされ、^{[ 3 ]}「最後のものとその前のものの和が次のマートラ・ヴリッタの番号である」と書いている。^{[ 15 ] [ 16 ]}

ヨーロッパ

フィレンツェ国立図書館所蔵のフィボナッチの算盤の書のページ。右のボックス内にフィボナッチ数列の 13 項目が示されています。現在から XII (月) までのインデックスはラテン序数とローマ数字で、数字 (ウサギのペア) は 1、2、3、5 から始まり 377 で終わるヒンドゥー教-アラビア数字で表されています。

フィボナッチ数列は、フィボナッチの著書「算数の書」（1202年）に初めて登場し、 [ 17 ] [ ^{18 ] 、ウサギの個体}数の増加を計算するために使用されています。^{[ 19 ]}フィボナッチは、理想的な（生物学的に非現実的な）ウサギの個体数の増加を考察し、次のような仮定をしています。生まれたばかりのウサギのつがいを野原に置きます。各つがいは生後1か月で交尾し、2か月目の終わりには必ずもう1つがいのウサギを産みます。ウサギは決して死なず、永遠に繁殖し続けます。フィボナッチはウサギの数学の問題を提起しました。1年間に何組のつがいが存在するでしょうか？

• 最初の月の終わりに彼らは交尾しますが、まだ 1 組しか残りません。
• 2 か月目の終わりには新しいペアが生まれるので、フィールドには 2 ペアが存在することになります。
• 3 か月目の終わりに、最初のペアは 2 番目のペアを産みますが、2 番目のペアは妊娠期間が 1 か月だけなので、全部で 3 ペアになります。
• 4 か月目の終わりには、最初のペアがさらに新しいペアを産み、2 か月前に生まれたペアも最初のペアを産み、ペアの数は 5 組になります。

n月の終わりには、ウサギのつがいの数は、成熟したつがいの数（つまり、n - 2月のつがいの数）と、前月（n - 1月）に生存していたつがいの数の合計に等しくなります。n月の数はn番目のフィボナッチ数です。^{[ 20 ]}

「フィボナッチ数列」という名称は、19世紀の数論学者エドゥアール・リュカスによって初めて使用されました。^{[ 21 ]}

フィボナッチ・ウサギ問題の解：理想的な集団が成長すると、ウサギのペアの数はフィボナッチ数列を形成します。nヶ月目の終わりには、ペアの数はF _{n に等しくなります。}

黄金比との関係

閉じた形式の表現

定数係数を持つ同次線形回帰によって定義されるすべての数列と同様に、フィボナッチ数は閉じた形式の表現を持ちます。^{[ 22 ]}これはフランスの数学者ジャック・フィリップ・マリー・ビネにちなんでビネの公式として知られていますが、アブラアン・ド・モアブルとダニエル・ベルヌーイによってすでに知られていました。^{[ 23 ]}

$${\displaystyle F_{n}={\frac {\varphi ^{n}-\psi ^{n}}{\varphi -\psi }}={\frac {\varphi ^{n}-\psi ^{n}}{\sqrt {5}}},}$$

ここで⁠ ⁠${\displaystyle \varphi}$ は黄金比、⁠ ⁠${\displaystyle \psi}$ はその共役比である。^{[ 24 ]}

$${\displaystyle {\begin{aligned}\varphi &={\tfrac {1}{2}}{\bigl (}1+{\sqrt {5}}~\!{\bigr )}={\phantom {-}}1.61803\ldots ,\\[5mu]\psi &={\tfrac {1}{2}}{\bigl (}1-{\sqrt {5}}~\!{\bigr )}=-0.61803\ldots .\end{aligned}}}$$ 数⁠ ⁠${\displaystyle \varphi}$ と⁠ ⁠ は、${\displaystyle \psi}$ 二次方程式⁠ ⁠${\displaystyle \textstyle x^{2}-x-1=0}$ の 2 つの解、つまり⁠ ⁠${\displaystyle (x-\varphi)(x-\psi)=x^{2}-x-1}$ であり、したがって、恒等式⁠ ⁠${\displaystyle \varphi +\psi =1}$ および⁠ ⁠${\displaystyle \varphi \psi =-1}$ を満たします。

なので、ビネの公式は次のようにも書ける。 ${\displaystyle \psi =-\varphi ^{-1}}$

$${\displaystyle F_{n}={\frac {\varphi ^{n}-(-\varphi )^{-n}}{\sqrt {5}}}={\frac {\varphi ^{n}-(-\varphi )^{-n}}{2\varphi -1}}.}$$

数列とこれらの定数の関係を見るために、^{[ 25 ]}と は の根でもあるのでとのべき乗はフィボナッチ再帰性を満たすことに注意する。言い換えれば、 ${\displaystyle \varphi}$ ${\displaystyle \psi}$ ${\displaystyle x^{n}=x^{n-1}+x^{n-2},}$ ${\displaystyle \varphi}$ ${\displaystyle \psi}$

$${\displaystyle {\begin{aligned}\varphi^{n}&=\varphi^{n-1}+\varphi^{n-2},\\[3mu]\psi^{n}&=\psi^{n-1}+\psi^{n-2}.\end{aligned}}}$$

任意の 値aとbに対して、

$${\displaystyle U_{n}=a\varphi ^{n}+b\psi ^{n}}$$

は同じ再帰性を満たす。aとbをU 0 ₌ 0かつU ₁ = 1となるように選ぶと、結果として得られる数列U _nは必ずフィボナッチ数列となる。これは、 aとbが以下の連立方程式を満たすことを 要求するのと同じである。

$${\displaystyle {\begin{aligned}a\varphi ^{0}+b\psi ^{0}&=0\\a\varphi ^{1}+b\psi ^{1}&=1\end{aligned}}}$$

解は

$${\displaystyle a={\frac {1}{\varphi -\psi }}={\frac {1}{\sqrt {5}}},\quad b=-a,}$$

必要な式を生成します。

初期値U ₀とU ₁を任意の定数とし、連立方程式を解くと一般解が得られます。 特に、a = 1を選択すると、 nが十分に大きい場合、数列のn番目の要素は⁠ ⁠のn乗に近似します。これは、 U ₀ = 2およびU ₁ = 1のときに発生し、ルーカス数列を生成し ます$${\displaystyle {\begin{aligned}a&={\frac {U_{1}-U_{0}\psi }{\sqrt {5}}},\\[3mu]b&={\frac {U_{0}\varphi -U_{1}}{\sqrt {5}}}.\end{aligned}}}$$ ${\displaystyle \varphi }$

四捨五入による計算

n ≥ 0の場合には、 F n_はに最も近い整数となる。したがって、最も近い整数関数を用いて を 四捨五入することで、F n を求めることができる。${\textstyle \left|{\frac {\psi ^{n}}{\sqrt {5}}}\right|<{\frac {1}{2}}}$ ${\displaystyle {\frac {\varphi ^{n}}{\sqrt {5}}}}$ $${\displaystyle F_{n}=\left\lfloor {\frac {\varphi ^{n}}{\sqrt {5}}}\right\rceil ,\ n\geq 0.}$$

実際、 nが大きくなるにつれて丸め誤差は急速に小さくなり、 n ≥ 4では0.1未満、 n ≥ 8では0.01未満になります。この式は簡単に逆変換でき、フィボナッチ数Fの指数を求めることができます。 $${\displaystyle n(F)=\left\lfloor \log _{\varphi }{\sqrt {5}}F\right\rceil ,\ F\geq 1.}$$

代わりに床関数を使用すると、F以下のフィボナッチ数の最大指数が得られます。 ここで、、、^{[ 26 ]}および。^{[ 27 ]}$${\displaystyle n_{\mathrm {largest} }(F)=\left\lfloor \log _{\varphi }{\sqrt {5}}(F+1/2)\right\rfloor ,\ F\geq 0,}$$ ${\displaystyle \log _{\varphi }(x)=\ln(x)/\ln(\varphi )=\log _{10}(x)/\log _{10}(\varphi )}$ ${\displaystyle \ln(\varphi )=0.481211\ldots }$ ${\displaystyle \log _{10}(\varphi )=0.208987\ldots }$

大きさ

F _{n は}に漸近するので、F _nの桁数はに漸近します。結果として、すべての整数d > 1に対して、小数点 以下d桁のフィボナッチ数は 4 個または 5 個存在します${\displaystyle \varphi ^{n}/{\sqrt {5}}}$ ${\displaystyle n\log _{10}\varphi \approx 0.2090\,n}$

より一般的には、b基底表現では、 F _nの桁数は漸近的に${\displaystyle n\log _{b}\varphi ={\frac {n\log \varphi }{\log b}}.}$

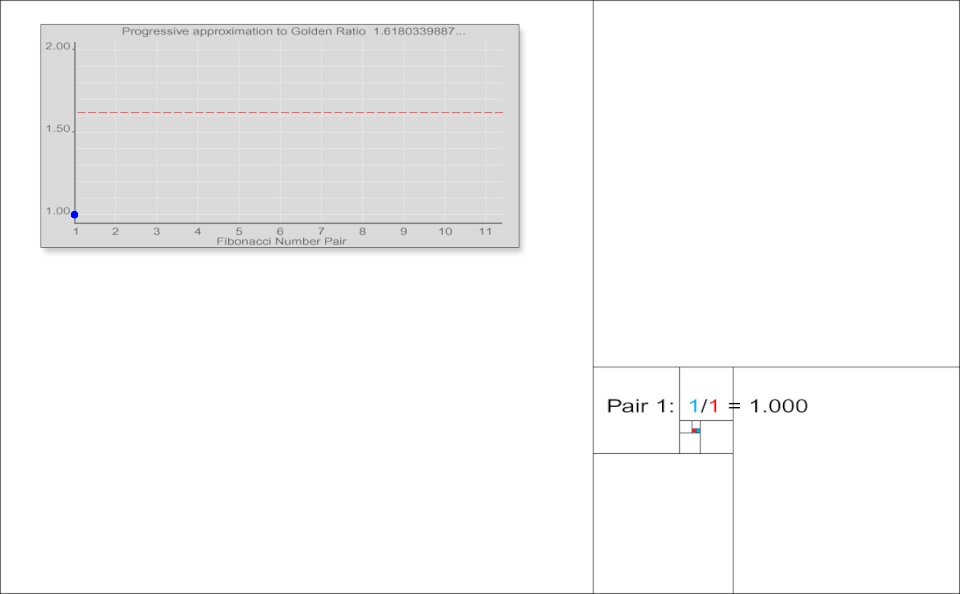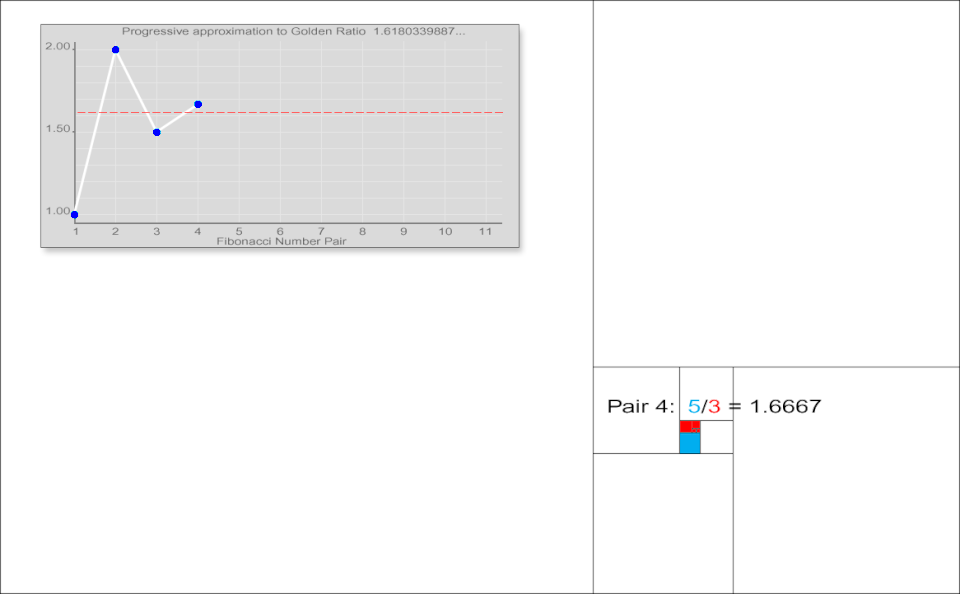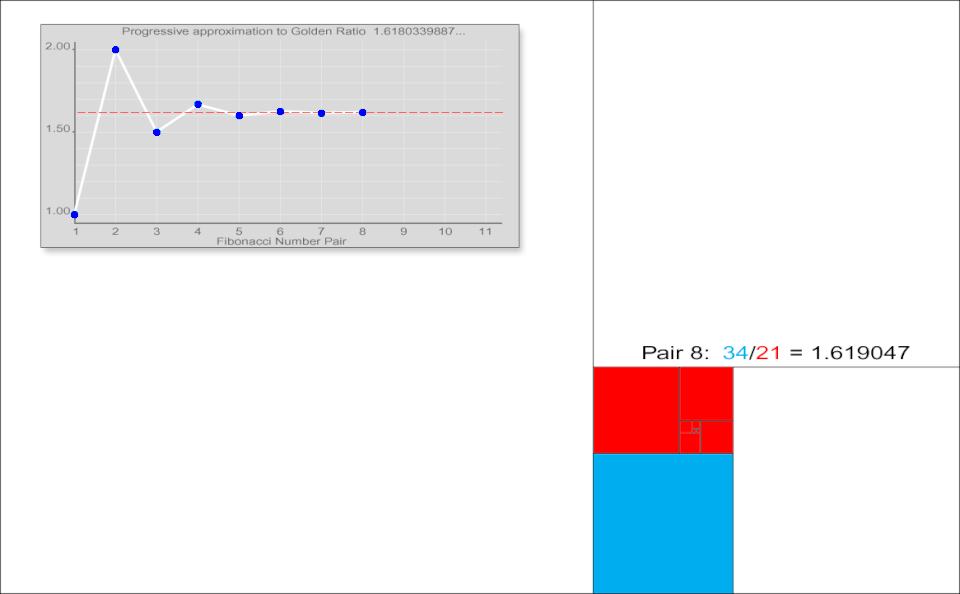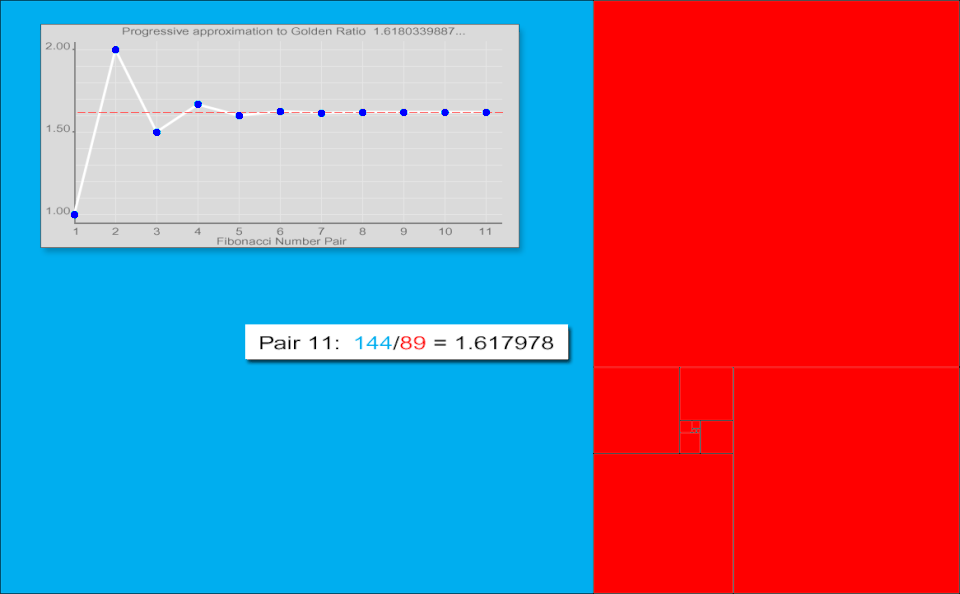
連続商の極限

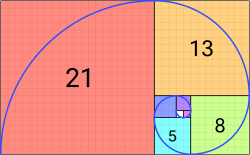
ヨハネス・ケプラーは、連続するフィボナッチ数の比が収束することを観察しました。彼は「5と8の比は、実質的には8と13の比と同じであり、8と13の比は、ほぼ13と21の比と同じである」と記し、これらの比は黄金比に近づくと結論付けました。${\displaystyle \varphi }$ ^{[ 28 ] [ 29 ]}$${\displaystyle \lim _{n\to \infty }{\frac {F_{n+1}}{F_{n}}}=\varphi .}$$

この収束は、の場合を除き、初期値と に関わらず成立します。これはビネの公式を用いて検証できます。例えば、初期値3と2から、3、2、5、7、12、19、31、50、81、131、212、343、555、…という数列が生成されます。この数列における連続する要素の比は、黄金比への同様の収束を示します。 ${\displaystyle U_{0}}$ ${\displaystyle U_{1}}$ ${\displaystyle U_{1}=-U_{0}/\varphi }$

一般に、連続するフィボナッチ数列間の比率は に近づくため、 となります。 ${\displaystyle \lim _{n\to \infty }{\frac {F_{n+m}}{F_{n}}}=\varphi ^{m}}$ ${\displaystyle \varphi }$

平面の連続したタイリングと、各フィボナッチ数を前の数で割ることによって計算された黄金比の近似値のグラフ

べき乗分解

黄金比は次の式を満たすので $${\displaystyle \varphi ^{2}=\varphi +1,}$$

この式は、高次のべき乗を低次のべき乗の線形関数として分解するのに使用でき、さらに、と1の線形結合まで分解できます。結果として得られる漸化式は、線形係数としてフィボナッチ数をもたらします。 この式は、 n ≥ 1の帰納法によって証明 できます。 の場合、また、また、 ${\displaystyle \varphi ^{n}}$ ${\displaystyle \varphi }$ $${\displaystyle \varphi ^{n}=F_{n}\varphi +F_{n-1}.}$$ $${\displaystyle {\begin{aligned}\varphi ^{n+1}&=(F_{n}\varphi +F_{n-1})\varphi =F_{n}\varphi ^{2}+F_{n-1}\varphi \\&=F_{n}(\varphi +1)+F_{n-1}\varphi =(F_{n}+F_{n-1})\varphi +F_{n}=F_{n+1}\varphi +F_{n}.\end{aligned}}}$$ ${\displaystyle \psi =-1/\varphi }$ ${\displaystyle \psi ^{2}=\psi +1}$ $${\displaystyle \psi ^{n}=F_{n}\psi +F_{n-1}.}$$

これらの式は、フィボナッチ数列F _{n が}フィボナッチの法則を用いて負の整数に拡張された場合、 n < 1に対しても成り立ちます。${\displaystyle F_{n}=F_{n+2}-F_{n+1}.}$

識別

ビネの公式は、正の整数xがフィボナッチ数であるためには、またはの少なくとも一方が完全な平方数である必要があります。^{[ 30 ]}これは、と書けるビネの公式が、を掛けて、二次方程式の公式を介して、の二次方程式として解くことができるためです ${\displaystyle 5x^{2}+4}$ ${\displaystyle 5x^{2}-4}$ ${\displaystyle F_{n}=(\varphi ^{n}-(-1)^{n}\varphi ^{-n})/{\sqrt {5}}}$ ${\displaystyle {\sqrt {5}}\varphi ^{n}}$ ${\displaystyle \varphi ^{n}}$

$${\displaystyle \varphi ^{n}={\frac {F_{n}{\sqrt {5}}\pm {\sqrt {5{F_{n}}^{\!2}+4(-1)^{n}}}}{2}}.}$$

これをと比較すると、 ${\displaystyle \varphi ^{n}=F_{n}\varphi +F_{n-1}=(F_{n}{\sqrt {5}}+F_{n}+2F_{n-1})/2}$

$${\displaystyle 5{F_{n}}^{\!2}+4(-1)^{n}=(F_{n}+2F_{n-1})^{2}\,.}$$

特に、左側は完全な正方形です。

行列形式

フィボナッチ数列を記述する 2次元線形差分方程式系は

$${\displaystyle {\begin{pmatrix}F_{k+2}\\F_{k+1}\end{pmatrix}}={\begin{pmatrix}1&1\\1&0\end{pmatrix}}{\begin{pmatrix}F_{k+1}\\F_{k}\end{pmatrix}}}$$ あるいは表記される $${\displaystyle {\vec {F}}_{k+1}=\mathbf {A} {\vec {F}}_{k},}$$

となり、行列Aの固有値はそれぞれ固有ベクトルに対応し、となる${\displaystyle {\vec {F}}_{n}=\mathbf {A} ^{n}{\vec {F}}_{0}}$ ${\displaystyle \varphi ={\tfrac {1}{2}}{\bigl (}1+{\sqrt {5}}~\!{\bigr )}}$ ${\displaystyle \psi =-\varphi ^{-1}={\tfrac {1}{2}}{\bigl (}1-{\sqrt {5}}~\!{\bigr )}}$ $${\displaystyle {\vec {\mu }}={\begin{pmatrix}\varphi \\1\end{pmatrix}},\quad {\vec {\nu }}={\begin{pmatrix}-\varphi ^{-1}\\1\end{pmatrix}}.}$$

初期値は なので 、n番目の要素は $${\displaystyle {\vec {F}}_{0}={\begin{pmatrix}1\\0\end{pmatrix}}={\frac {1}{\sqrt {5}}}{\vec {\mu }}\,-\,{\frac {1}{\sqrt {5}}}{\vec {\nu }},}$$ $${\displaystyle {\begin{aligned}{\vec {F}}_{n}\ &={\frac {1}{\sqrt {5}}}A^{n}{\vec {\mu }}-{\frac {1}{\sqrt {5}}}A^{n}{\vec {\nu }}\\&={\frac {1}{\sqrt {5}}}\varphi ^{n}{\vec {\mu }}-{\frac {1}{\sqrt {5}}}(-\varphi )^{-n}{\vec {\nu }}\\&={\cfrac {1}{\sqrt {5}}}\left({\cfrac {1+{\sqrt {5}}}{2}}\right)^{\!n}{\begin{pmatrix}\varphi \\1\end{pmatrix}}\,-\,{\cfrac {1}{\sqrt {5}}}\left({\cfrac {1-{\sqrt {5}}}{2}}\right)^{\!n}{\begin{pmatrix}{c}-\varphi ^{-1}\\1\end{pmatrix}}.\end{aligned}}}$$

このことから、フィボナッチ数列のn番目の要素は、閉じた形式の式として直接読み取ることができます。 $${\displaystyle F_{n}={\cfrac {1}{\sqrt {5}}}\left({\cfrac {1+{\sqrt {5}}}{2}}\right)^{\!n}-\,{\cfrac {1}{\sqrt {5}}}\left({\cfrac {1-{\sqrt {5}}}{2}}\right)^{\!n}.}$$

同様に、Aの固有分解を用いてAを対角化することでも同じ計算が行えます。 ここで 、フィボナッチ数列の n番目の要素 の閉じた表現は 次のように与えられ、これもまた次の式 になります。$${\displaystyle {\begin{aligned}A&=S\Lambda S^{-1},\\[3mu]A^{n}&=S\Lambda ^{n}S^{-1},\end{aligned}}}$$ $${\displaystyle \Lambda ={\begin{pmatrix}\varphi &0\\0&-\varphi ^{-1}\!\end{pmatrix}},\quad S={\begin{pmatrix}\varphi &-\varphi ^{-1}\\1&1\end{pmatrix}}.}$$ $${\displaystyle {\begin{aligned}{\begin{pmatrix}F_{n+1}\\F_{n}\end{pmatrix}}&=A^{n}{\begin{pmatrix}F_{1}\\F_{0}\end{pmatrix}}\ \\&=S\Lambda ^{n}S^{-1}{\begin{pmatrix}F_{1}\\F_{0}\end{pmatrix}}\\&=S{\begin{pmatrix}\varphi ^{n}&0\\0&(-\varphi )^{-n}\end{pmatrix}}S^{-1}{\begin{pmatrix}F_{1}\\F_{0}\end{pmatrix}}\\&={\begin{pmatrix}\varphi &-\varphi ^{-1}\\1&1\end{pmatrix}}{\begin{pmatrix}\varphi ^{n}&0\\0&(-\varphi )^{-n}\end{pmatrix}}{\frac {1}{\sqrt {5}}}{\begin{pmatrix}1&\varphi ^{-1}\\-1&\varphi \end{pmatrix}}{\begin{pmatrix}1\\0\end{pmatrix}},\end{aligned}}}$$ $${\displaystyle F_{n}={\cfrac {\varphi ^{n}-(-\varphi )^{-n}}{\sqrt {5}}}.}$$

行列Aの行列式は-1なので、 2×2ユニモジュラ行列です。

この性質は、黄金比φの連分数表現で理解できます。 φの連分数の収束点は 、連続するフィボナッチ数列の比です。φ _n = F _{n +1} / F _nはn番目の収束点であり、( n + 1)番目の収束点は、再帰関係φ _{n +1} = 1 + 1 / φ _nから見つけることができます。^{[ 31 ]}任意の連分数の連続する収束点から形成される行列の行列式は、+1 または -1 です。 行列表現により、フィボナッチ数列の次の閉じた形式の式が得られます。 与えられたnに対して、この行列は、2乗法による累乗を使用して、O (log n )回の算術演算で計算できます。 ^{[ b ]}$${\displaystyle \varphi =1+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{1+\ddots }}}}}}.}$$ $${\displaystyle {\begin{pmatrix}1&1\\1&0\end{pmatrix}}^{n}={\begin{pmatrix}F_{n+1}&F_{n}\\F_{n}&F_{n-1}\end{pmatrix}}.}$$

この方程式の両辺の行列式をとるとカシニの恒等式が得られる。 $${\displaystyle (-1)^{n}=F_{n+1}F_{n-1}-{F_{n}}^{2}.}$$

さらに、任意の正方行列Aに対してA ⁿ A ^m = A ^{n + m}であるため、次の恒等式が導出されます（これらは行列積の2つの異なる係数から得られ、 n をn + 1に変更することで最初の係数から2番目の係数を簡単に導き出すことができます）。 $${\displaystyle {\begin{aligned}{F_{m}}{F_{n}}+{F_{m-1}}{F_{n-1}}&=F_{m+n-1},\\[3mu]F_{m}F_{n+1}+F_{m-1}F_{n}&=F_{m+n}.\end{aligned}}}$$

特に、m = nの場合には、 $${\displaystyle {\begin{aligned}F_{2n-1}&={F_{n}}^{2}+{F_{n-1}}^{2}\\[6mu]F_{2n{\phantom {{}-1}}}&=(F_{n-1}+F_{n+1})F_{n}\\[3mu]&=(2F_{n-1}+F_{n})F_{n}\\[3mu]&=(2F_{n+1}-F_{n})F_{n}.\end{aligned}}}$$

これらの最後の2つの恒等式は、O (log n )回の演算でフィボナッチ数を再帰的に計算する方法を提供します。これは、閉形式行列式からn番目のフィボナッチ数を計算するのに要する時間とほぼ一致しますが、既に計算済みのフィボナッチ数の再計算（メモ化を伴う再帰）を避ければ、冗長なステップ数が少なくなります。^{[ 32 ]}

組合せ論的恒等式

組合せ論的証明

フィボナッチ数列を含むほとんどの恒等式は、が となるような（空である可能性のある）1と2の列の個数として解釈できるという事実を用いた組合せ論的議論によって証明できる。これは、という規則の下で の定義と見なすことができ、これは、和が -1 となるような列は存在しないことを意味し、 は、空列の「合計」が 0 になることを意味する。以下では、は集合の濃度である。 ${\displaystyle F_{n}}$ ${\displaystyle n-1}$ ${\displaystyle F_{n}}$ ${\displaystyle F_{0}=0}$ ${\displaystyle F_{1}=1}$ ${\displaystyle |{...}|}$

${\displaystyle F_{0}=0=|\{\}|}$

${\displaystyle F_{1}=1=|\{()\}|}$

${\displaystyle F_{2}=1=|\{(1)\}|}$

${\displaystyle F_{3}=2=|\{(1,1),(2)\}|}$

${\displaystyle F_{4}=3=|\{(1,1,1),(1,2),(2,1)\}|}$

${\displaystyle F_{5}=5=|\{(1,1,1,1),(1,1,2),(1,2,1),(2,1,1),(2,2)\}|}$

このように、 すべてのシーケンスが 1 または 2 で始まる 2 つの重複しないセットにシーケンスを 分割することによって、再帰関係を理解できます。 最初の要素を除いて、各シーケンスの残りの項の合計はまたはになり、各セットの基数はまたはとなり、シーケンスの合計は となり、これは に等しいことがわかります。 $${\displaystyle F_{n}=F_{n-1}+F_{n-2}}$$ ${\displaystyle F_{n}}$ $${\displaystyle F_{n}=|\{(1,...),(1,...),...\}|+|\{(2,...),(2,...),...\}|}$$ ${\displaystyle n-2}$ ${\displaystyle n-3}$ ${\displaystyle F_{n-1}}$ ${\displaystyle F_{n-2}}$ ${\displaystyle F_{n-1}+F_{n-2}}$ ${\displaystyle F_{n}}$

同様に、最初のフィボナッチ数からn番目までの和は、 ( n +2)番目のフィボナッチ数から1を引いた値に等しいことが示される。 ^{[ 33 ]} 記号で表すと、 $${\displaystyle \sum _{i=1}^{n}F_{i}=F_{n+2}-1}$$

これは、最初の 2 つの位置に基づいて、合計がとなるすべてのシーケンスを分割することで確認できます。具体的には、各セットは、それぞれカーディナリティが 1 である最後の 2 つのセットまで始まるシーケンスで構成されます。 ${\displaystyle n+1}$ ${\displaystyle (2,...),(1,2,...),...,}$ ${\displaystyle \{(1,1,...,1,2)\},\{(1,1,...,1)\}}$

先ほどと同じ論理に従って、各集合の濃度を合計すると、

${\displaystyle F_{n+2}=F_{n}+F_{n-1}+...+|\{(1,1,...,1,2)\}|+|\{(1,1,...,1)\}|}$

...ここで最後の2つの項の値は です。このことから となります。 ${\displaystyle F_{1}=1}$ ${\displaystyle \sum _{i=1}^{n}F_{i}=F_{n+2}-1}$

同様の議論で、最初の 2 ではなく最初の 1 の位置で合計をグループ化すると、さらに 2 つの恒等式が得られます。 言葉で言え ば 、最初の奇数指数 のフィボナッチ数の合計は(2 n )番目のフィボナッチ数であり、最初の偶数指数のフィボナッチ数の合計は(2 n + 1)番目のフィボナッチ数から 1 を引いた値です。 ^{[ 34 ]}$${\displaystyle \sum _{i=0}^{n-1}F_{2i+1}=F_{2n}}$$ $${\displaystyle \sum _{i=1}^{n}F_{2i}=F_{2n+1}-1.}$$ ${\displaystyle F_{2n-1}}$ ${\displaystyle F_{2n}}$

証明には別のトリックを使うことができます。 あるいは言葉で言えば、最初のフィボナッチ数列の平方の和は、 n番目と( n +1)番目のフィボナッチ数の積です。これを確認するには、まずサイズのフィボナッチ長方形を から始めて、それを の正方形に分解します。すると、面積を比較することで等式が導かれます。 $${\displaystyle \sum _{i=1}^{n}F_{i}^{2}=F_{n}F_{n+1}}$$ ${\displaystyle F_{n}}$ ${\displaystyle F_{n}\times F_{n+1}}$ ${\displaystyle F_{n},F_{n-1},...,F_{1}}$

帰納法による証明

フィボナッチ等式は、 数学的帰納法を使って簡単に証明できることが多いです

例えば、 両辺を 足し合わせると$${\displaystyle \sum _{i=1}^{n}F_{i}=F_{n+2}-1.}$$ ${\displaystyle F_{n+1}}$

${\displaystyle \sum _{i=1}^{n}F_{i}+F_{n+1}=F_{n+1}+F_{n+2}-1}$

そして次の式が得られます${\displaystyle n+1}$ $${\displaystyle \sum _{i=1}^{n+1}F_{i}=F_{n+3}-1}$$

同様に、の両辺に 足し て ${\displaystyle {F_{n+1}}^{2}}$ $${\displaystyle \sum _{i=1}^{n}F_{i}^{2}=F_{n}F_{n+1}}$$ $${\displaystyle \sum _{i=1}^{n}F_{i}^{2}+{F_{n+1}}^{2}=F_{n+1}\left(F_{n}+F_{n+1}\right)}$$ $${\displaystyle \sum _{i=1}^{n+1}F_{i}^{2}=F_{n+1}F_{n+2}}$$

ビネの公式の証明

ビネの公式は、 フィボナッチ等式を証明するために使用できます $${\displaystyle {\sqrt {5}}F_{n}=\varphi ^{n}-\psi ^{n}.}$$

たとえば、 事実と方程式を簡略 化して、 左辺に を掛けると になること に留意して証明します。${\textstyle \sum _{i=1}^{n}F_{i}=F_{n+2}-1}$ ${\displaystyle {\sqrt {5}}}$ $${\displaystyle {\begin{aligned}1+&\varphi +\varphi ^{2}+\dots +\varphi ^{n}-\left(1+\psi +\psi ^{2}+\dots +\psi ^{n}\right)\\&={\frac {\varphi ^{n+1}-1}{\varphi -1}}-{\frac {\psi ^{n+1}-1}{\psi -1}}\\&={\frac {\varphi ^{n+1}-1}{-\psi }}-{\frac {\psi ^{n+1}-1}{-\varphi }}\\&={\frac {-\varphi ^{n+2}+\varphi +\psi ^{n+2}-\psi }{\varphi \psi }}\\&=\varphi ^{n+2}-\psi ^{n+2}-(\varphi -\psi )\\&={\sqrt {5}}(F_{n+2}-1)\\\end{aligned}}}$$ ${\textstyle \varphi \psi =-1}$ ${\textstyle \varphi -\psi ={\sqrt {5}}}$

その他のアイデンティティ

様々な方法を用いて、他にも多数のアイデンティティを導き出すことができます。そのいくつかを以下に示します。^{[ 35 ]}

カッシーニとカタランの正体

カッシーニの恒等式は、 カタランの恒等式が一般化されていると述べています。 $${\displaystyle F_{n}^{2}-F_{n+1}F_{n-1}=(-1)^{n-1}}$$ $${\displaystyle F_{n}^{2}-F_{n+r}F_{n-r}=(-1)^{n-r}F_{r}^{2}}$$

ドカーニュの恒等式

$${\displaystyle F_{m}F_{n+1}-F_{m+1}F_{n}=(-1)^{n}F_{m-n}}$$ $${\displaystyle F_{2n}=F_{n+1}^{2}-F_{n-1}^{2}=F_{n}\left(F_{n+1}+F_{n-1}\right)=F_{n}L_{n}}$$ ここで、L _nはn次のルーカス数です。最後のはnを2倍した場合の恒等式です。このタイプの他の恒等式は カッシーニの恒等式によって 得られます$${\displaystyle F_{3n}=2F_{n}^{3}+3F_{n}F_{n+1}F_{n-1}=5F_{n}^{3}+3(-1)^{n}F_{n}}$$

$${\displaystyle F_{3n+1}=F_{n+1}^{3}+3F_{n+1}F_{n}^{2}-F_{n}^{3}}$$ $${\displaystyle F_{3n+2}={F_{n+1}}^{3}+3F_{n+1}^{2}F_{n}+F_{n}^{3}}$$ $${\displaystyle F_{4n}=4F_{n}F_{n+1}\left(F_{n+1}^{2}+2F_{n}^{2}\right)-3F_{n}^{2}\left(F_{n}^{2}+2F_{n+1}^{2}\right)}$$ これらは格子縮小法 を使って実験的に見つけることができ、フィボナッチ数を 因数分解するための特殊数体ふるいを設定する際に役立ちます。

より一般的には、^{[ 35 ]}

$${\displaystyle F_{kn+c}=\sum _{i=0}^{k}{\binom {k}{i}}F_{c-i}F_{n}^{i}F_{n+1}^{k-i}.}$$

または、代わりに

$${\displaystyle F_{kn+c}=\sum _{i=0}^{k}{\binom {k}{i}}F_{c+i}F_{n}^{i}F_{n-1}^{k-i}.}$$

この式にk = 2を代入すると、上記のセクションの最後の行列形式の式が再び得られます

生成関数

通常

フィボナッチ数列の通常の生成関数は、べき級数です

$${\displaystyle s(z)=\sum _{k=0}^{\infty }F_{k}z^{k}=0+z+z^{2}+2z^{3}+3z^{4}+5z^{5}+\cdots .}$$

この級数は任意の複素数 に対して収束し、その和は単純な閉形式を持つ：^{[ 36 ]}${\displaystyle z}$ ${\displaystyle |z|<1/\varphi \approx 0.618,}$

$${\displaystyle s(z)={\frac {z}{1-z-z^{2}}}.}$$

これは を掛けることで証明できます。 ここで を含むすべての項は、定義上のフィボナッチ再帰関係により打ち消されます 。${\textstyle (1-z-z^{2})}$ $${\displaystyle {\begin{aligned}(1-z-z^{2})s(z)&=\sum _{k=0}^{\infty }F_{k}z^{k}-\sum _{k=0}^{\infty }F_{k}z^{k+1}-\sum _{k=0}^{\infty }F_{k}z^{k+2}\\&=\sum _{k=0}^{\infty }F_{k}z^{k}-\sum _{k=1}^{\infty }F_{k-1}z^{k}-\sum _{k=2}^{\infty }F_{k-2}z^{k}\\&=0z^{0}+1z^{1}-0z^{1}+\sum _{k=2}^{\infty }(F_{k}-F_{k-1}-F_{k-2})z^{k}\\&=z,\end{aligned}}}$$ ${\displaystyle z^{k}}$ ${\displaystyle k\geq 2}$

を使用すると、フィボナッチ数列から最後から2番目の数までを の小数展開で表すことができます。例えば、${\displaystyle z={10}^{-n}}$ ${\displaystyle n}$ ${\displaystyle s(z)}$ $${\displaystyle s(10^{-3})={\frac {0.001}{0.998999}}={\frac {1000}{998999}}=000.\,001\,001\,002\,003\,005\,008\,013\,\ldots .}$$

部分分数分解は、 が黄金比、 がその共役で あるで与えられます 。 $${\displaystyle s(z)={\frac {1}{\sqrt {5}}}\left({\frac {1}{1-\varphi z}}-{\frac {1}{1-\psi z}}\right)}$$ ${\textstyle \varphi ={\tfrac {1}{2}}\left(1+{\sqrt {5}}\right)}$ ${\displaystyle \psi ={\tfrac {1}{2}}\left(1-{\sqrt {5}}\right)}$

指数関数

フィボナッチ数列の指数関数的生成関数は、漸化式から導出することもでき、同次線型微分方程式を与える。 この方程式の特性多項式は であり、その解は黄金比とその共役と全く同じである。初期値 および と組み合わせると、フィボナッチ数列の指数関数的生成関数は、関数全体で与えられる。指数関数的生成関数の導関数を で 評価すると、ビネの公式が得られる。 $${\displaystyle {\begin{aligned}\sum _{k=0}^{\infty }F_{k+2}{\frac {x^{k}}{k!}}={}&\sum _{k=0}^{\infty }F_{k+1}{\frac {x^{k}}{k!}}+\sum _{k=0}^{\infty }F_{k}{\frac {x^{k}}{k!}}\\F^{\prime \prime }(x)={}&F^{\prime }(x)+F(x)\end{aligned}}}$$ ${\textstyle r^{2}=r+1}$ ${\textstyle \varphi }$ ${\textstyle \psi }$ ${\textstyle F_{0}=F(0)=0}$ ${\textstyle F_{1}=F^{\prime }(0)=1}$ $${\displaystyle F(x)={\frac {e^{\varphi x}-e^{\psi x}}{\sqrt {5}}}}$$ ${\textstyle x=0}$ $${\displaystyle F^{(n)}(0)=F_{n}={\frac {\varphi ^{n}-\psi ^{n}}{\sqrt {5}}}}$$

逆数和

フィボナッチ数の逆数にわたる無限和は、シータ関数で評価できる場合があります。例えば、すべての奇数添字のフィボナッチ数の逆数和は次のように表すことができます $${\displaystyle \sum _{k=1}^{\infty }{\frac {1}{F_{2k-1}}}={\frac {\sqrt {5}}{4}}\;\vartheta _{2}\!\left(0,{\frac {3-{\sqrt {5}}}{2}}\right)^{2},}$$

そしてフィボナッチ数の逆数の二乗の和は $${\displaystyle \sum _{k=1}^{\infty }{\frac {1}{{F_{k}}^{2}}}={\frac {5}{24}}\!\left(\vartheta _{2}\!\left(0,{\frac {3-{\sqrt {5}}}{2}}\right)^{4}-\vartheta _{4}\!\left(0,{\frac {3-{\sqrt {5}}}{2}}\right)^{4}+1\right).}$$

最初の合計の各フィボナッチ数に1を加えると、閉じた形も存在する。 $${\displaystyle \sum _{k=1}^{\infty }{\frac {1}{1+F_{2k-1}}}={\frac {\sqrt {5}}{2}},}$$

そして、フィボナッチ数の二乗の和が入れ子になっており、黄金比の逆数となる。 $${\displaystyle \sum _{k=1}^{\infty }{\frac {(-1)^{k+1}}{\sum _{j=1}^{k}{F_{j}}^{2}}}={\frac {{\sqrt {5}}-1}{2}}.}$$

すべての偶数添字の逆フィボナッチ数の和はランバート級数 と^{[ 37 ]} 同じである。$${\displaystyle \sum _{k=1}^{\infty }{\frac {1}{F_{2k}}}={\sqrt {5}}\left(L(\psi ^{2})-L(\psi ^{4})\right)}$$ ${\displaystyle \textstyle L(q):=\sum _{k=1}^{\infty }{\frac {q^{k}}{1-q^{k}}},}$ ${\displaystyle \textstyle {\frac {1}{F_{2k}}}={\sqrt {5}}\left({\frac {\psi ^{2k}}{1-\psi ^{2k}}}-{\frac {\psi ^{4k}}{1-\psi ^{4k}}}\right)\!.}$

フィボナッチ定数の逆数は^{[ 38 ]}$${\displaystyle \sum _{k=1}^{\infty }{\frac {1}{F_{k}}}=\sum _{k=1}^{\infty }{\frac {1}{F_{2k-1}}}+\sum _{k=1}^{\infty }{\frac {1}{F_{2k}}}=3.359885666243\dots }$$

さらに、この数はリチャード・アンドレ＝ジャンナンによって無理数であることが証明されている。^{[ 39 ]}

ミリン級数は、 Nが無限大に近づく につれて、その部分和の閉じた形式から従う恒等式^{[ 40 ]} を与える。 $${\displaystyle \sum _{k=0}^{\infty }{\frac {1}{F_{2^{k}}}}={\frac {7-{\sqrt {5}}}{2}},}$$ $${\displaystyle \sum _{k=0}^{N}{\frac {1}{F_{2^{k}}}}=3-{\frac {F_{2^{N}-1}}{F_{2^{N}}}}.}$$

素数と割り切れる数

割り切れる

特に、連続する3つのフィボナッチ数は互いに素である。なぜなら、 と は互いに素だからである。つまり、${\displaystyle F_{3}=2}$ $${\displaystyle \gcd(F_{a},F_{b},F_{c},\ldots )=F_{\gcd(a,b,c,\ldots )}\,}$$ ${\displaystyle F_{0}=1}$ ${\displaystyle F_{1}=1}$

すべてのnについて。${\displaystyle F_{1}=1}$ ${\displaystyle F_{2}=1}$

${\displaystyle \gcd(F_{n},F_{n+1})=\gcd(F_{n},F_{n+2})=\gcd(F_{n+1},F_{n+2})=1}$

for every n.

すべての素数p は、p を  5 で割った値で決まるフィボナッチ数を割り切れます。p が 5 を法として 1 または 4 と合同である場合、 pはF p −1_{を割り切れ}ます。また、 pが 5 を法として 2 または 3 と合同である場合、p はF _{p +1}を割り切れます。残りのケースはp = 5 の場合で、この場合はpはF _pを割り切れます。

$${\displaystyle {\begin{cases}p=5&\Rightarrow p\mid F_{p},\\p\equiv \pm 1{\pmod {5}}&\Rightarrow p\mid F_{p-1},\\p\equiv \pm 2{\pmod {5}}&\Rightarrow p\mid F_{p+1}.\end{cases}}}$$

これらのケースは、ルジャンドル記号を使って、単一の非区分式にまとめることができる。^{[ 43 ]}$${\displaystyle p\mid F_{p\,-~\!\left({\frac {5}{p}}\right)}.}$$

素数判定

上記の式は、ルジャンドル記号をヤコビ記号 に置き換えた場合、nが素数であることの証拠となり、成り立たない場合、nは明らかに素数ではないという意味で 、素数判定として使用できます。nが合成数で、この式を満たす場合、nはフィボナッチ擬素数です。mが大きい場合（たとえば500ビットの数）、行列形式を使用してF _m (mod n )を効率的に計算できます。したがって $${\displaystyle n\mid F_{n\,-~\!\left({\frac {5}{n}}\right)},}$$

$${\displaystyle {\begin{pmatrix}F_{m+1}&F_{m}\\F_{m}&F_{m-1}\end{pmatrix}}\equiv {\begin{pmatrix}1&1\\1&0\end{pmatrix}}^{m}{\pmod {n}}.}$$ ここで行列のべき乗A ^mはべき乗剰余を用いて計算され、これは行列に適応することができる。^{[ 44 ]}

フィボナッチ素数

フィボナッチ素数とは、素数であるフィボナッチ数です。最初のいくつかは次のとおりです。^{[ 45 ]}

2、3、5、13、89、233、1597、28657、514229、...

数千桁のフィボナッチ素数は発見されているが、無限に存在するかどうかは分かっていない。^{[ 46 ]}

F _knはF _nで割り切れるので、 F ₄ = 3を除き、あらゆるフィボナッチ素数は必ず素数指数を持つ。合成数には任意の長さの連続、合成フィボナッチ数にも任意の長さの連続が存在する。

F6 =8より大きいフィボナッチ数は、素数より1大きくも1小さくもありませ_ん。^{[ 47 ]}

唯一の非自明な平方フィボナッチ数は144である。^{[ 48 ]} Attila Pethőは2001年に完全べきフィボナッチ数 は有限個しか存在しないことを証明した。^{[ 49 ]} 2006年に、Y. Bugeaud、M. Mignotte、S. Siksekは8と144が唯一の非自明な完全べき数であることを証明した。^{[ 50 ]}

1、3、21、55は唯一の三角形のフィボナッチ数であり、これはヴァーン・ホガットによって予想され、羅明によって証明された。^{[ 51 ]}

フィボナッチ数は完全数にはなり得ない。^{[ 52 ]}より一般的には、1以外のフィボナッチ数は完全倍数にはなり得ず、^{[ 53 ]} 2つのフィボナッチ数の比も完全数にはなり得ない。^{[ 54 ]}

素因数

1、8、144（F ₁ = F ₂、F ₆、F ₁₂）を除いて、すべてのフィボナッチ数には、それより小さいフィボナッチ数の因数ではない素因数があります（カーマイケルの定理）。^{[ 55 ]}その結果、8と144（F ₆とF ₁₂）は、他のフィボナッチ数の積となる唯一のフィボナッチ数です。^{[ 56 ]}

フィボナッチ数が素数pで割り切れるかどうかは、次のように評価される ルジャンドル記号 と関係があります。${\displaystyle {\bigl (}{\tfrac {p}{5}}{\bigr )}}$ $${\displaystyle \left({\frac {p}{5}}\right)={\begin{cases}0&{\text{if }}p=5\\1&{\text{if }}p\equiv \pm 1{\pmod {5}}\\-1&{\text{if }}p\equiv \pm 2{\pmod {5}}.\end{cases}}}$$

pが素数 ならば^{[ 57 ] [ 58 ]}$${\displaystyle F_{p}\equiv \left({\frac {p}{5}}\right){\pmod {p}}\quad {\text{and}}\quad F_{p-\left({\frac {p}{5}}\right)}\equiv 0{\pmod {p}}.}$$

例えば、 $${\displaystyle {\begin{aligned}{\bigl (}{\tfrac {2}{5}}{\bigr )}&=-1,&F_{3}&=2,&F_{2}&=1,\\{\bigl (}{\tfrac {3}{5}}{\bigr )}&=-1,&F_{4}&=3,&F_{3}&=2,\\{\bigl (}{\tfrac {5}{5}}{\bigr )}&=0,&F_{5}&=5,\\{\bigl (}{\tfrac {7}{5}}{\bigr )}&=-1,&F_{8}&=21,&F_{7}&=13,\\{\bigl (}{\tfrac {11}{5}}{\bigr )}&=+1,&F_{10}&=55,&F_{11}&=89.\end{aligned}}}$$

素数pが存在するかどうかは 不明です

$${\displaystyle F_{p\,-~\!\left({\frac {p}{5}}\right)}\equiv 0{\pmod {p^{2}}}.}$$

そのような素数は（もし存在するならば）ウォール・サン・サン素数と呼ばれるでしょう。

また、p ≠5が奇数の素数である場合は^{[ 59 ]}$${\displaystyle 5{F_{\frac {p\pm 1}{2}}}^{2}\equiv {\begin{cases}{\tfrac {1}{2}}\left(5{\bigl (}{\tfrac {p}{5}}{\bigr )}\pm 5\right){\pmod {p}}&{\text{if }}p\equiv 1{\pmod {4}}\\{\tfrac {1}{2}}\left(5{\bigl (}{\tfrac {p}{5}}{\bigr )}\mp 3\right){\pmod {p}}&{\text{if }}p\equiv 3{\pmod {4}}.\end{cases}}}$$

例 1. p = 7、この場合p ≡ 3 (mod 4)となり、次の式が成り立ちます。 $${\displaystyle {\bigl (}{\tfrac {7}{5}}{\bigr )}=-1:\qquad {\tfrac {1}{2}}\left(5{\bigl (}{\tfrac {7}{5}}{\bigr )}+3\right)=-1,\quad {\tfrac {1}{2}}\left(5{\bigl (}{\tfrac {7}{5}}{\bigr )}-3\right)=-4.}$$ $${\displaystyle F_{3}=2{\text{ and }}F_{4}=3.}$$ $${\displaystyle 5{F_{3}}^{2}=20\equiv -1{\pmod {7}}\;\;{\text{ and }}\;\;5{F_{4}}^{2}=45\equiv -4{\pmod {7}}}$$

例2. p = 11、この場合p≡3（mod 4）となり、次の式が成り立ちます。 $${\displaystyle {\bigl (}{\tfrac {11}{5}}{\bigr )}=+1:\qquad {\tfrac {1}{2}}\left(5{\bigl (}{\tfrac {11}{5}}{\bigr )}+3\right)=4,\quad {\tfrac {1}{2}}\left(5{\bigl (}{\tfrac {11}{5}}{\bigr )}-3\right)=1.}$$ $${\displaystyle F_{5}=5{\text{ and }}F_{6}=8.}$$ $${\displaystyle 5{F_{5}}^{2}=125\equiv 4{\pmod {11}}\;\;{\text{ and }}\;\;5{F_{6}}^{2}=320\equiv 1{\pmod {11}}}$$

例3. p = 13、この場合p≡1（mod 4）となり、次の式が成り立ちます。 $${\displaystyle {\bigl (}{\tfrac {13}{5}}{\bigr )}=-1:\qquad {\tfrac {1}{2}}\left(5{\bigl (}{\tfrac {13}{5}}{\bigr )}-5\right)=-5,\quad {\tfrac {1}{2}}\left(5{\bigl (}{\tfrac {13}{5}}{\bigr )}+5\right)=0.}$$ $${\displaystyle F_{6}=8{\text{ and }}F_{7}=13.}$$ $${\displaystyle 5{F_{6}}^{2}=320\equiv -5{\pmod {13}}\;\;{\text{ and }}\;\;5{F_{7}}^{2}=845\equiv 0{\pmod {13}}}$$

例4. p = 29、この場合p≡1（mod 4）となり、次の式が成り立ちます。 $${\displaystyle {\bigl (}{\tfrac {29}{5}}{\bigr )}=+1:\qquad {\tfrac {1}{2}}\left(5{\bigl (}{\tfrac {29}{5}}{\bigr )}-5\right)=0,\quad {\tfrac {1}{2}}\left(5{\bigl (}{\tfrac {29}{5}}{\bigr )}+5\right)=5.}$$ $${\displaystyle F_{14}=377{\text{ and }}F_{15}=610.}$$ $${\displaystyle 5{F_{14}}^{2}=710645\equiv 0{\pmod {29}}\;\;{\text{ and }}\;\;5{F_{15}}^{2}=1860500\equiv 5{\pmod {29}}}$$

nが奇数の場合、 Fnのすべての奇数素因数は₄を法として1と合同であり、これはFnのすべての奇数約数（奇数素因数の積として）が4を法として1と合同である_{ことを意味する。} ^{[ 60 ]}

例えば、 $${\displaystyle F_{1}=1,\ F_{3}=2,\ F_{5}=5,\ F_{7}=13,\ F_{9}={\color {Red}34}=2\cdot 17,\ F_{11}=89,\ F_{13}=233,\ F_{15}={\color {Red}610}=2\cdot 5\cdot 61.}$$

フィボナッチ数F ( i ) （ i < 50000 ）のすべての既知の因数は、関連するリポジトリに収集されています。^{[ 61 ] [ 62 ]}

nを法とした周期性

フィボナッチ数列の要素を nを法としてとると、得られる数列は周期的となり、その周期は最大で 6 nとなる。^{[ 63 ]}様々なnに対する周期の長さは、いわゆるピサノ周期と呼ばれる。^{[ 64 ]}ピサノ周期の一般公式を決定することは未解決問題であり、そのサブ問題として、モジュラー整数または有限体上の元の乗法順序を求める問題の特殊な例が含まれる。しかし、任意の特定のnに対して、ピサノ周期はサイクル検出の例として見出すことができる。

一般化

フィボナッチ数列は、漸化式、具体的には線形差分方程式によって定義される、最も単純かつ最も古くから知られている数列の1つです。これらの数列はすべて、フィボナッチ数列の一般化と見なすことができます。特に、ビネーの公式は、定数 係数を持つ同次線形差分方程式の解である任意の数列に一般化できます

ある意味でフィボナッチ数列に近い具体的な例としては、次のようなものがあります。

• インデックスを負の整数に一般化して、ネガフィボナッチ数を生成します。
• ビネの公式の修正を用いて指数を実数に一般化する。 ^{[ 35 ]}
• 他の整数から始めます。ルーカス数はL ₁ = 1、L ₂ = 3、L _n = L _{n −1} + L _{n −2}です。プライムフリー数列は、他の開始点とフィボナッチ再帰を用いて、すべての数が合成数となる数列を生成します。
• ある数を、その前の2つの数の線形関数（和以外）とします。ペル数はP _n = 2 P _{n −1} + P _{n −2}です。前の値の係数に変数xを割り当てると、結果はフィボナッチ多項式の数列になります。
• 直前の数字を加算しない。パドヴァン数列とペラン数はP ( n ) = P ( n − 2) + P ( n − 3)となる。
• 3つの数（トリボナッチ数）、4つの数（テトラナッチ数）、あるいはそれ以上の数を足し合わせて次の数を生成する。結果として得られる数列はnステップフィボナッチ数として知られる。^{[ 65 ]}

応用

数学

フィボナッチ数は、左揃えのパスカルの三角形の対角線（赤で表示）の和です

フィボナッチ数はパスカルの三角形の「浅い」対角線の二項係数の和として現れる。^{[ 66 ]}これは生成関数を展開し 、の同類項を集めること で証明できる 。 $${\displaystyle F_{n}=\sum _{k=0}^{\left\lfloor {\frac {n-1}{2}}\right\rfloor }{\binom {n-k-1}{k}}.}$$ $${\displaystyle {\frac {x}{1-x-x^{2}}}=x+x^{2}(1+x)+x^{3}(1+x)^{2}+\dots +x^{k+1}(1+x)^{k}+\dots =\sum \limits _{n=0}^{\infty }F_{n}x^{n}}$$ ${\displaystyle x^{n}}$

この式がどのように使用されるかを確認するには、存在する項の数によって合計を並べます。

5	= 1+1+1+1+1
	= 2+1+1+1	= 1+2+1+1	= 1+1+2+1	= 1+1+1+2
	= 2+2+1	= 2+1+2	= 1+2+2

これは、 n − k −1個の項 からk個の 2 の位置を選択していることになります${\displaystyle \textstyle {\binom {5}{0}}+{\binom {4}{1}}+{\binom {3}{2}}}$

フィボナッチ数列を用いて{1, 2}-制限合成を数える

^{これらの数は特定の列挙問題[ 67 ]}の解も与えます。最も一般的な問題は、与えられた数nを1と2の順序付けられた和（合成と呼ばれる）として表す方法の数を数える問題です。これにはFn _{+ 1}通りの方法があります（これは長方形のドミノタイルの数でもあります）。例えば、5段の階段を1段または2段ずつ登る方法 はF5 _{+1 =} F6 = 8通りあります。${\displaystyle 2\times n}$

5	= 1+1+1+1+1	= 2+1+1+1	= 1+2+1+1	= 1+1+2+1	= 2+2+1
	= 1+1+1+2	= 2+1+2	= 1+2+2

図は、8を5（4段登った後に1段登る方法の数）と3（3段登った後に2段登る方法の数）に分解できることを示しています。同じ推論が再帰的に適用され、1段登る方法は1つしかありません。

フィボナッチ数は、バイナリ文字列のセット内、または同等に、特定のセットの サブセット内において、さまざまな方法で見つけることができます。

• 連続する1のない長さnのバイナリ文字列の数は、フィボナッチ数F _{n +2}です。たとえば、長さ 4 の 16 個のバイナリ文字列のうち、連続する1のないものはF ₆ = 8 個あります。これらは、 0000、0001、0010、0100、0101、1000、1001、1010です。このような文字列は、フィボナッチ数のバイナリ表現です。同様に、F _{n +2}は、連続する整数のない{1, ..., n }の部分集合Sの数、つまり、すべてのiについて{ i、i + 1} ⊈ Sとなるような部分集合Sの数です。n +1への和の一対一変換は、 1 を0に、 2 を10に置き換え、最後のゼロを削除することです。
• 長さnのバイナリ文字列のうち、連続する1が奇数個ない文字列の数はフィボナッチ数F _{n +1}です。例えば、長さ 4 のバイナリ文字列 16 個のうち、連続する1が奇数個ない文字列はF ₅ = 5 個あります。これらは0000、0011、0110、1100、1111です。同様に、 {1, ..., n }の部分集合Sのうち、連続する整数が奇数個ない文字列の数はF _{n +1}です。n への一対一の和は、 1 を0に、 2 を11に置き換えることです。
• 長さnのバイナリ文字列のうち、連続する0または1が偶数個ない文字列の数は2 F _{n 個}です。例えば、長さ 4 のバイナリ文字列 16 個のうち、連続する0または1が偶数個ない文字列は2 F ₄ = 6 個あります。つまり、 0001、0111、0101、1000、1010、1110です。部分集合についても同様のことが言えます。
• ユーリ・マティヤセヴィッチはフィボナッチ数がディオファントス方程式で定義できることを示すことができ、それがヒルベルトの第10問題の解決 につながった。^{[ 68 ]}
• フィボナッチ数列もまた、完全数列の一例です。これは、すべての正の整数がフィボナッチ数列の和として表すことができ、どの数も最大で一度しか使用されないことを意味します。
• さらに、すべての正の整数は、1つ以上の異なるフィボナッチ数の和として一意に表すことができます。ただし、その和には連続する2つのフィボナッチ数が含まれません。これはゼッケンドルフの定理として知られており、これらの条件を満たすフィボナッチ数の和はゼッケンドルフ表現と呼ばれます。ある数のゼッケンドルフ表現は、そのフィボナッチ符号化を導くために使用できます。
• 5から始めて、2番目ごとのフィボナッチ数は、整数の辺を持つ直角三角形の斜辺の長さ、つまり、式から得られるピタゴラスの三つ組の最大の数です。この式から得られるピタゴラス三角形の列は、辺の長さが(3,4,5)、(5,12,13)​​、(16,30,34)、(39,80,89)、...です。これらの三角形のそれぞれの中辺は、前の三角形の3辺の和です。^{[ 69 ]}$${\displaystyle (F_{n}F_{n+3})^{2}+(2F_{n+1}F_{n+2})^{2}={F_{2n+3}}^{2}.}$$
• フィボナッチキューブは、並列コンピューティングのネットワーク トポロジとして提案されている、フィボナッチ数のノードを持つ無向グラフです。
• フィボナッチ数は環の補題に現れ、円充填定理と等角写像の関係を証明するのに用いられる。^{[ 70 ]}

コンピュータサイエンス

高さ6のフィボナッチツリー。バランス係数は緑、高さは赤です。左背表紙のキーはフィボナッチ数です

• フィボナッチ数は、 2つの整数の最大公約数を決定するユークリッドのアルゴリズムの計算実行時解析において重要です。このアルゴリズムの最悪の入力は、連続するフィボナッチ数のペアです。^{[ 71 ]}
• フィボナッチ数は、マージソートアルゴリズムの多相バージョンで使用されます。このアルゴリズムでは、ソートされていないリストを、フィボナッチ数の連続する長さに対応する2つのリストに分割します。つまり、リストを2つの部分の長さがほぼφの比率になるように分割します。この多相マージソートのテープドライブ実装は、『The Art of Computer Programming』で説明されています。
• フィボナッチ木は、子木の高さが（再帰的に）ちょうど1ずつ異なる二分木です。したがって、これはAVL木であり、与えられた高さに対して最も少ないノードを持つ木、つまり「最も薄い」AVL木です。これらの木は、フィボナッチ数から1を引いた数の頂点を持ち、これはAVL木の解析において重要な事実です。^{[ 72 ]}
• フィボナッチ数は、いくつかの疑似乱数ジェネレータによって使用されます。
• フィボナッチ数は、フィボナッチ ヒープデータ構造の解析で発生します。
• フィボナッチ探索法と呼ばれる1次元最適化手法では、フィボナッチ数列が使用されます。^{[ 73 ]}
• フィボナッチ数列は、Amigaコンピュータで使用されるIFF 8SVXオーディオファイルフォーマットにおけるオプションの非可逆圧縮に使用されます。この数列は、μ-lawなどの対数法と同様に、元のオーディオ波形を圧縮します。^{[ 74 ] [ 75 ]}
• 一部のアジャイルチームは、プランニングポーカーにおいて「修正フィボナッチ数列」と呼ばれる修正された数列を見積もりツールとして用いています。プランニングポーカーは、Scaled Agile Frameworkの正式な一部です。^{[ 76 ]}
• フィボナッチ・コーディング
• ネガフィボナッチ・コーディング

自然

黄色いカモミールの花穂に、21（青）と13（水色）の螺旋状の配列が見られます。連続したフィボナッチ数列を含むこのような配列は、さまざまな植物に見られます

フィボナッチ数列は生物学的な場面に現れ、^{[ 77 ]}樹木の枝分かれ、茎の葉の配置、パイナップルの小果実、^{[ 78 ]}アーティチョークの開花、アロエ（Aloe polyphylla）の葉^{[ 79 ]} 、松ぼっくりの配置、^{[ 80 ]}ミツバチの系統樹などである。^{[ 81 ] [ 82 ]}ケプラーは自然界にフィボナッチ数列が存在することを指摘し、それを使って一部の花の（黄金比に関連した）五角形の形状を説明しました。^{[ 83 ]}野生のヒナギクはほとんどの場合、フィボナッチ数列の花びらを持っています。^{[ 84 ]} 1830年、カール・フリードリヒ・シンパーとアレクサンダー・ブラウンは植物の寄生（螺旋葉序）がフィボナッチ数列を含む分数として頻繁に表現されることを発見しました。 ^{[ 85 ]}

プシェミスワフ・プルシンキェヴィチは、実インスタンスは部分的には自由群に対する特定の代数的制約の表現、具体的には特定のリンデンマイヤー文法として理解できるという考えを提唱した。^{[ 86 ]}

n = 1 ... 500の Vogel モデルの図解

ヒマワリの頭花のパターンのモデルは、 1979年にヘルムート・フォーゲルによって提案されました。^{[ 87 ]} これは次のような形をしています。

$${\displaystyle \theta ={\frac {2\pi }{\varphi ^{2}}}n,\ r=c{\sqrt {n}}}$$

ここで、nは小花のインデックス番号、cは定数のスケーリング係数です。したがって、小花はフェルマーの螺旋上にあります。発散角は約 137.51° で、円を黄金比で分割する黄金角です。この比は無理数なので、中心からまったく同じ角度に隣接する小花はなく、小花は効率的に詰め込まれます。黄金比の有理近似はF ( j ): F ( j + 1)の形式であるため、小花番号nに最も近い隣接小花は、中心からの距離rに依存するインデックスjに対して、 n ± F ( j )にある小花です。ヒマワリやそれに似た花では、隣接するフィボナッチ数列の数だけ時計回りと反時計回りの方向に小花の螺旋が最も一般的に見られ、^{[ 88 ]}通常は最も外側の半径の範囲で数えられます。^{[ 89 ]}

フィボナッチ数は、次の規則に従って、 ハチ（半二倍体）の祖先の系図にも現れます。

• 卵が産まれても受精しない場合は、雄蜂（ミツバチの場合は雄蜂）が生まれます。
• しかし、卵子が受精すると雌が生まれます。

したがって、オスの蜂には必ず親が 1 人、メスの蜂には親が 2 人います。どのオスの蜂 (1 匹) の血統をたどっても、親が 1 人 (1 匹)、祖父母が 2 人、曽祖父母が 3 人、高祖父母が 5 人、というように続きます。この親の数の並びはフィボナッチ数列です。各レベルの祖先の数F _nは、メスの祖先の数F _{n −1}とオスの祖先の数F _{n −2}を足した数です。^{[ 90 ] [ 91 ]}これは、各レベルの祖先はそれ以外は無関係であるという非現実的な仮定に基づいています。

ある祖先世代におけるX染色体遺伝線上の祖先の数はフィボナッチ数列に従う。（ハッチソン、L.「家系図の育成：家族関係の再構築におけるDNAの力」^{[ 92 ]}より）

同様に、ある祖先世代におけるヒトのX染色体遺伝系統上の祖先の可能な数もフィボナッチ数列に従うことが指摘されている。 ^{[ 92 ]}男性は母親から受け継いだX染色体と父親から受け継いだY染色体を持つ。男性は自身のX染色体の「起源」（ ）として数えられ、その親の世代では、その男性のX染色体は片親（）に由来する。男性の母親は、その母親（息子の母方の祖母）から1本のX染色体を、その父親（息子の母方の祖父）から1本を受け継いでいるため、2人の祖父母が男性の子孫のX染色体（）に寄与していることになる。母方の祖父は母親からX染色体を受け継ぎ、母方の祖母は両親からX染色体を受け継いでいるため、男性の子孫のX染色体（）には3人の曽祖父母が寄与している。男性の子孫のX染色体（）には5人の高祖父母が寄与している、などとなる。（これは、特定の子孫のすべての祖先が独立していると仮定しているが、系図を十分に遡ると、祖先が系図の複数の系統に現れ始め、最終的には集団の創始者が系図のすべての系統に現れるようになる。） ${\displaystyle F_{1}=1}$ ${\displaystyle F_{2}=1}$ ${\displaystyle F_{3}=2}$ ${\displaystyle F_{4}=3}$ ${\displaystyle F_{5}=5}$

その他

• 光学において、光線が屈折率の異なる異なる材料で作られた2枚の透明板を斜めに透過すると、2枚の板の上面、中間面、下面の3つの面で反射することがあります。k > 1の場合、k回の反射を持つ異なる光線経路の数は、k番目のフィボナッチ数です。（ただし、k = 1の場合、反射経路は2つではなく3つあり、3つの面それぞれに1つずつあります。）^{[ 93 ]}
• フィボナッチ リトレースメントレベルは、金融市場取引のテクニカル分析で広く使用されています。
• マイルからキロメートルへの変換係数1.609344は黄金比に近いため、マイル単位の距離をフィボナッチ数列の和に分解すると、フィボナッチ数を後続の数列に置き換えることで、ほぼキロメートル単位の和となる。この方法は、黄金比を底とするφの基数2の数値レジスタをシフトすることになる。キロメートルからマイルに変換するには、代わりにレジスタをフィボナッチ数列に沿ってシフトする。^{[ 94 ]}
• 無限抵抗連鎖回路（抵抗ラダー回路または無限直並列回路とも呼ばれる）における電圧と電流の測定値はフィボナッチ数列に従う。直列抵抗と並列抵抗を交互に加算した中間結果は、連続するフィボナッチ数列からなる分数となる。回路全体の等価抵抗は黄金比に等しい。^{[ 95 ]}
• Brasch et al. 2012 は、一般化フィボナッチ数列が経済学の分野にもどのように関連しているかを示している。^{[ 96 ]}特に、一般化フィボナッチ数列が、1つの状態と1つの制御変数を持つ有限時間領域動的最適化問題の制御関数にどのように組み込まれるかが示されている。この手順は、ブロック・ミルマン経済成長モデルと呼ばれる例で説明されている。
• マリオ・メルツは1970年代から彼の作品のいくつかにフィボナッチ数列を取り入れました。^{[ 97 ]}
• ジョセフ・シリンガー（1895-1943）は、いくつかのメロディーにフィボナッチ音程を使用する作曲システムを考案しました。彼はこれを、自然界に見られる精巧なハーモニーの音楽的対応物と見なしました。 ^{[ 98 ]}黄金比§音楽も参照してください。
• ソフトウェア開発において、フィボナッチ数はスクラムフレームワークで活動するアジャイルチームによって、製品バックログ項目のサイズを決定するためによく使用されます。^{[ 99 ]}

参照

• フィボナッチ協会 – フィボナッチ数列の研究組織
• 大衆文化におけるフィボナッチ数列
• フィボナッチ語 – フィボナッチ再帰からの2進数列
• ランダムフィボナッチ数列 – フィボナッチ数列に基づいたランダムな数学的数列
• ウィトフ配列 – フィボナッチ数列から導かれる整数の無限行列
• フィボナッチ数とその応用に関する国際会議 – 数学会議

参考文献

解説脚注

1. 「4の場合、2拍子と3拍子の韻律のバリエーションが混ざり合って5拍子になります。5の場合、前の2拍子のバリエーション、つまり3拍子と4拍子が混ざり合って8拍子になります。このように、6の場合、4拍子と5拍子のバリエーションが混ざり合って13拍子になります。そして同様に、前の2拍子のバリエーションが混ざり合って7拍子で21拍子になります。このように、すべてのマートラ・ヴリッタにおいてこのプロセスに従うべきです。」 ^{[ 14 ]}
2. 任意精度の算術演算はO (1)とみなされます。ビット長を考慮すると、2乗による累乗は依然として大幅な改善ですが、全体的な計算量は最後の乗算ステップによって支配されます。結果にはO ( n )桁の桁があり、タスクではそれらすべてを生成する必要があります。

引用

1. リチャード・A・ブルーディ著『入門組合せ論』第5版、ピアソン、2005年
2. ピーター・キャメロン著『組合せ論：トピック、テクニック、アルゴリズム』ケンブリッジ大学出版局、1994年
3. Goonatilake、Susantha (1998)、Toward a Global Science、インディアナ大学出版局、p. 126、ISBN 978-0-253-33388-9
4. Singh, Parmanand (1985)、「古代および中世インドにおけるいわゆるフィボナッチ数」、Historia Mathematica、12 (3): 229– 244、doi : 10.1016/0315-0860(85)90021-7
5. クヌース、ドナルド（2006年）、コンピュータプログラミングの芸術、第4巻。すべての木を生成する - 組み合わせ生成の歴史、アディソン・ウェズレー、p. 50、ISBN 978-0-321-33570-8、m拍の[L]と[S]のすべてのシーケンスの集合を考えるのは自然なことでした。…それらはFm+1個あります。例えば、m = 7の場合の21個のシーケンスは次のとおりです。[リストを示す]。このようにして、インドの韻律学者は、セクション1.2.8（v.1より）で述べたように、フィボナッチ数列を発見するに至りました
6. シグラー 2002、404～405頁。
7. ルーカス 1891、3ページ。
8. ベック＆ジオゲガン 2010 .
9. ボナ 2011、180頁。
10. ヴァイダ、スティーブン（1989年）『フィボナッチ数とルーカス数、そして黄金比：理論と応用』チチェスター：エリス・ホーウッド、p.10、ISBN 0-7458-0715-1。
11. ドナルド・クヌース（1968年）『コンピュータプログラミングの芸術』第1巻、アディソン・ウェスレー、100ページ、ISBN 978-81-7758-754-8フィボナッチが著作を書く以前から、数列Fnはインドの学者によってすでに議論されており、彼らは長い間リズムパターンに興味を持っていました…ゴパーラ（西暦1135年以前）とヘマチャンドラ（1150年頃）はどちらも1、2、3、5、8、13、21という数字を明示的に言及しています[P. Singh Historia Math 12 (1985) 229–44] p. 100 (第3版)…
12. リビオ 2003、p. 197。
13. アグラワラ、VS（1969）、パーニカーリーナ・バーラタヴァルシャ（Hn.）。バラナシ-I：チャウカンバ・ヴィディヤバワンにおいて、サドグルシ・シャは、ピンガラはパーニニの弟であると記している[アグラワラ 1969, lb]。一方、彼はパーニニの母方の叔父であったという説もある[ヴィナヤサガル 1965, 序文, 121]。…アグラワラ[1969, 463–76]は、先人の学者たちの見解を考慮した慎重な調査の結果、パーニニは紀元前480年から410年の間に生きたと結論付けている。
14. ヴェランカー、HD（1962）、カビ・ヴィラハンカ​​の「Vṛttajātisamuccaya」、ジョードプル：ラジャスタン東洋研究所、p. 101
15. リヴィオ 2003、197–198ページ。
16. Shah, Jayant (1991), A History of Piṅgala's Combinatorics (PDF) , Northeastern University , p. 41 , 2019-01-04取得
17. シグラー 2002、404–405頁。
18. 「フィボナッチの算盤（計算書）」ユタ大学、2009年12月13日、 2018年11月28日閲覧。
19. タッソーン、アン・ドミニク（1967年4月）「ウサギのペアと数学者」『算数教師』14（4）：285-288、doi：10.5951/at.14.4.0285、JSTOR 41187298 
20. ノット、ロン、『フィボナッチのウサギ』、サリー大学工学・物理科学部
21. ガードナー、マーティン（1996）、数学サーカス、アメリカ数学協会、p.153、ISBN 978-0-88385-506-5 数学に貴重な貢献をしたレオナルドが、今日では主に19世紀のフランスの数論学者エドゥアール・リュカスが『アバカスの書』の簡単な問題に登場する数列にフィボナッチという名前を付けたことで記憶されているというのは皮肉なことです
22. ベルカストロ、サラ・マリー(2018). 『アヒルと学ぶ離散数学』（第2版）CRC Press. p. 260. ISBN 978-1-351-68369-2。260ページの抜粋
23. Beutelspacher, Albrecht; Petri, Bernhard (1996)、「Fibonacci-Zahlen」、Der Goldene Schnitt、Einblick in die Wissenschaft、Vieweg+Teubner Verlag、pp.  87– 98、doi : 10.1007/978-3-322-85165-9_6、ISBN 978-3-8154-2511-4
24. ボール 2003、156ページ
25. ボール 2003、155～156ページ
26. Sloane, N. J. A. (編), 「シーケンス A002390 (黄金比の自然対数の小数展開)」 ,オンライン整数シーケンス百科事典, OEIS Foundation
27. Sloane, N. J. A. (編), 「シーケンス A097348 (arccsch(2)/log(10) の小数展開)」 ,オンライン整数シーケンス百科事典, OEIS Foundation
28. ケプラー、ヨハネス（1966年）、A New Year Gift: On Hexagonal Snow、オックスフォード大学出版局、p. 92、ISBN 978-0-19-858120-8
29. Strena seu de Nive Sexangula、1611
30. ゲッセル、アイラ（1972年10月）「フィボナッチは2乗である」（PDF）、フィボナッチ・クォータリー、10（4）：417-19 、 2012年4月11日閲覧。
31. 「黄金比、フィボナッチ数列、連分数」nrich.maths.org . 2024年3月22日閲覧。
32. ダイクストラ、エドガー W. (1978)「フィボナッチに敬意を表して」 (PDF)
33. ルーカス 1891、4ページ。
34. ヴォロビエフ、ニコライ・ニコラエヴィチ; Martin、Mircea (2002)、「第 1 章」、フィボナッチ数列、Birkhäuser、pp.  5–6、ISBN 978-3-7643-6135-8
35. ワイススタイン、エリック・W.、「フィボナッチ数」、MathWorld
36. Glaister, P (1995)、「フィボナッチ冪級数」、The Mathematical Gazette、79 (486): 521–25、doi : 10.2307/3618079、JSTOR 3618079、S2CID 116536130  
37. Landau (1899)はBorweinの95ページ、演習3bに従って引用されている。
38. Sloane, N. J. A. (編), 「数列 A079586 (Sum_{k>=1} 1/F(k) の小数展開。ここで F(k) はk番目のフィボナッチ数)」 ,オンライン整数数列百科事典, OEIS Foundation
39. André-Jeannin、Richard (1989)、「Irrationalité de la somme des inverses de somees suites récurrentes」、Comptes Rendus de l'Académie des Sciences、Série I、308 (19): 539–41、MR 0999451 
40. ホンスバーガー、ロス (1985)、「ミリンのシリーズ」、数学の宝石III、ドルチアーニ数学解説集、第9巻、アメリカ数学会、pp.  135– 136、ISBN 9781470457181
41. リーベンボイム、パウロ（2000年）『My Numbers, My Friends』、シュプリンガー・フェアラーク
42. Su, Francis E (2000)、「Fibonacci GCD's, please」、Mudd Math Fun Facts、他、HMC、2009年12月14日時点のオリジナルよりアーカイブ、2007年2月23日閲覧。
43. Williams, HC (1982)、「フィボナッチ商に関する注記」、Canadian Mathematical Bulletin、25 (3): 366– 70、doi : 10.4153/CMB-1982-053-0、hdl : 10338.dmlcz/137492、MR 0668957${\displaystyle F_{p-\varepsilon }/p}$  ウィリアムズはこの特性を「よく知られている」と呼んでいます。
44. 素数、リチャード・クランドール、カール・ポメランス、シュプリンガー、第2版、2005年、142ページ。
45. Sloane, N. J. A. (編)、「数列 A005478 (素数フィボナッチ数)」、オンライン整数数列百科事典、 OEIS Foundation
46. Diaconis, Persi (2018)、「Probabilizing Fibonacci numbers」（PDF）、Butler, Steve、Cooper, Joshua、Hurlbert, Glenn（編）、Connections in Discrete Mathematics: A Celebration of the Work of Ron Graham、Cambridge University Press、pp.  1– 12、ISBN 978-1-107-15398-1、MR  3821829 、 2023年11月18日にオリジナル（PDF）からアーカイブ、 2022年11月23日取得
47. ホンスバーガー、ロス（1985）、「数学の宝石III」、AMSドルチアーニ数学解説（9）：133、ISBN 978-0-88385-318-4
48. Cohn, JHE (1964)、「平方フィボナッチ数について」、ロンドン数学会誌、39 : 537–540、doi : 10.1112/jlms/s1-39.1.537、MR 0163867 
49. Pethő、Attila (2001)、「線形再帰シーケンスのディオファンティン特性 II」、Acta Mathematica Academiae Paedagogicae Nyíregyháziensis、17 : 81–96
50. Bugeaud, Y; Mignotte, M; Siksek, S (2006)、「指数ディオファントス方程式への古典的およびモジュラーアプローチ。I. フィボナッチとルーカスの完全べき乗」、Ann. Math.、2 (163): 969– 1018、arXiv : math/0403046、Bibcode : 2004math......3046B、doi : 10.4007/annals.2006.163.969、S2CID 10266596 
51. Luo, Ming (1989)、「三角フィボナッチ数について」(PDF)、Fibonacci Quart.、27 (2): 98– 108、doi : 10.1080/00150517.1989.12429576
52. Luca、Florian (2000)、「Perfect Fibonacci and Lucas Numbers」、Rendiconti del Circolo Matematico di Palermo、49 (2): 313–18、doi : 10.1007/BF02904236、ISSN 1973-4409、MR 1765401、S2CID 121789033   
53. Broughan, Kevin A.; González, Marcos J.; Lewis, Ryan H.; Luca, Florian; Mejía Huguet, V. Janitzio; Togbé, Alain (2011) 「多重完全フィボナッチ数は存在しない」『Integers』11a : A7, MR 2988067 
54. ルカ、フロリアン、メヒア・ユゲット、V. ジャニツィオ (2010)、「2つのフィボナッチ数の比である完全数について」、Annales Mathematicae at Informaticae、37 : 107–24、ISSN 1787-6117、MR 2753031  
55. ノット、ロン『フィボナッチ数列』、イギリス：サリー
56. Sloane, N. J. A. (編)、「数列 A235383 (他のフィボナッチ数の積であるフィボナッチ数)」、オンライン整数数列百科事典、 OEIS Foundation
57. リベンボイム、パウロ（1996）、素数記録の新書、ニューヨーク：シュプリンガー、p.64、ISBN 978-0-387-94457-9
58. レマーマイヤー 2000、73～74ページ、例2.25～28
59. Lemmermeyer 2000、pp.73-74、例2.28。
60. Lemmermeyer 2000、p.73、例2.27。
61. フィボナッチ因数分解とルーカス因数分解、メルセンヌスF ( i )の既知の因数のうちi < 10000 のものをすべて集める
62. フィボナッチ数とルーカス数の因数、Red golpe10000 < i < 50000のF ( i )の既知の因数をすべて集める
63. Freyd, Peter; Brown, Kevin S. (1993)、「問題と解答：解答：E3410」、アメリカ数学月刊誌、99 (3): 278–79、doi : 10.2307/2325076、JSTOR 2325076 
64. Sloane, N. J. A. (編)、「数列 A001175 (ピサノ周期 (またはピサノ数): nを法とするフィボナッチ数の周期)」、オンライン整数数列百科事典、 OEIS Foundation
65. Lü, Kebo; Wang, Jun (2006)、「kステップフィボナッチ数列の法m」、Utilitas Mathematica、71 : 169–177、MR 2278830 
66. ルーカス 1891、7ページ。
67. スタンレー、リチャード（2011）、列挙的組合せ論I（第2版）、ケンブリッジ大学出版局、p.121、Ex1.35、ISBN 978-1-107-60262-5
68. ハリザノフ、ヴァレンティーナ（1995） 「ユーリ・V・マティヤセヴィッチ著『ヒルベルトの第10問題』のレビュー」、モダン・ロジック、5（3）：345–55
69. パグニ、デイビッド（2001年9月）「フィボナッチとピタゴラスの出会い」『Mathematics in School』30（4）：39-40、JSTOR 30215477 
70. スティーブンソン、ケネス（2005）、サークルパッキング入門：離散解析関数の理論、ケンブリッジ大学出版局、ISBN 978-0-521-82356-2、MR  2131318特に補題8.2（環の補題）73～74ページ、および付録B「環の補題」318～321ページを参照
71. ドナルド・E・クヌース（1997年）『コンピュータプログラミングの芸術』第1巻：基礎アルゴリズム（第3版）、アディソン・ウェズレー、343ページ、ISBN 978-0-201-89683-1
72. アデルソン＝ヴェルスキー、ゲオルギー；ランディス、エフゲニー（1962）、「情報組織化のためのアルゴリズム」、ソ連科学アカデミー紀要（ロシア語）、146：263-266Myron J. Ricciによる英訳、Soviet Mathematics - Doklady、3:1259–1263、1962年。
73. アヴリエル、M; ワイルド、DJ (1966)、「対称フィボナッチ探索技法の最適性」、フィボナッチ・クォータリー(3): 265–69、doi : 10.1080/00150517.1966.12431364
74. Amiga ROMカーネルリファレンスマニュアル、Addison–Wesley、1991
75. 「IFF」、マルチメディアWiki
76. Dean Leffingwell (2021-07-01)、ストーリー、Scaled Agile Framework 、2022年8月15日閲覧
77. Douady, S; Couder, Y (1996)、「動的な自己組織化プロセスとしての葉序」（PDF）、Journal of Theoretical Biology、178（3）：255– 74、doi：10.1006/jtbi.1996.0026 、 2006年5月26日時点のオリジナル（PDF）からアーカイブ
78. ジョーンズ、ジュディ、ウィルソン、ウィリアム（2006年）「科学」、不完全な教育、バランタインブックス、544ページ、ISBN 978-0-7394-7582-9
79. 「私たちの庭園におけるフィボナッチの驚異｜カリフォルニア大学サンマテオ郡およびサンフランシスコ郡マスターガーデナーズ」ucanr.edu。2025年11月18日閲覧
80. Brousseau, A (1969)、「針葉樹のフィボナッチ統計」、フィボナッチ・クォータリー( 7): 525–32
81. 「ダ・ヴィンチ・コードの点数：B–」、数学、コンピュータサイエンス（趣味）：CS4FN
82. Scott, TC; Marketos, P. (2014年3月)、「フィボナッチ数列の起源について」 (PDF)、MacTutor数学史アーカイブ、セントアンドリュース大学
83. リヴィオ 2003、110ページ。
84. リヴィオ 2003、112～113頁。
85. Varenne、Franck (2010)、Formaliser le vivant - Lois、Théories、Modeles (フランス語)、Hermann、p. 28、ISBN 9782705678128、2022年10月30日取得、En 1830、KF Schimper et A. Braun [...]。Ils montraient que si l'on représente cet angle de divergence par une fraction reflétant le nombre de tours par feuille ([...]), on tombe régulièrement sur un des nombres de la suite de Fibonacci pour le numérateur [...]
86. Prusinkiewicz, Przemyslaw; Hanan, James (1989), Lindenmayer Systems, Fractals, and Plants (Lecture Notes in Biomathematics) , Springer-Verlag , ISBN 978-0-387-97092-9
87. Vogel, Helmut (1979)、「ヒマワリの頭を作るためのより良い方法」、Mathematical Biosciences、44 ( 3–4 ): 179–89、doi : 10.1016/0025-5564(79)90080-4
88. リヴィオ 2003、112ページ。
89. Prusinkiewicz, Przemyslaw ; Lindenmayer, Aristid (1990)、「4」、植物のアルゴリズム的美、Springer-Verlag、pp.  101–107、ISBN 978-0-387-97297-8
90. Basin, SL (1963)、「自然界に現れるフィボナッチ数列」(PDF)、The Fibonacci Quarterly、1 (1): 53– 56、doi : 10.1080/00150517.1963.12431602
91. Yanega, D. 1996. スズメバチ（膜翅目：ハチ科）における性比と性別配分. J. Kans. Ent. Soc. 69 Suppl.: 98-115.
92. ハッチソン、ルーク（2004年9月）「家系図の成長：家族関係の再構築におけるDNAの力」（PDF）、第1回バイオインフォマティクス・バイオテクノロジーシンポジウム（BIOT-04）の議事録、 2020年9月25日時点のオリジナル（PDF）からアーカイブ、 2016年9月3日取得
93. リヴィオ 2003、98～99頁。
94. 「ゼッケンドルフ表現」、数学百科事典
95. Patranabis, D.; Dana, SK (1985年12月)、「端子減衰測定とフィボナッチ数列を用いたシングルシャント故障診断」、IEEE Transactions on Instrumentation and Measurement、IM-34 (4): 650– 653、Bibcode : 1985ITIM...34..650P、doi : 10.1109/tim.1985.4315428、S2CID 35413237 
96. Brasch, T. von; Byström, J.; Lystad, LP (2012)、「最適制御とフィボナッチ数列」、Journal of Optimization Theory and Applications、154 (3): 857– 78、doi : 10.1007/s10957-012-0061-2、hdl : 11250/180781、S2CID 8550726 
97. リヴィオ 2003、176ページ。
98. リヴィオ 2003、193ページ。
99. Kathuria, Madhur. 「スクラムにおけるフィボナッチ数列の使用ガイド」 Scrum Alliance . 2025年8月8日閲覧。

引用文献

• ボール、キース・M（2003）、「8：フィボナッチのウサギ再考」、奇妙な曲線、ウサギの数え方、その他の数学的探究、プリンストン、ニュージャージー：プリンストン大学出版局、ISBN 978-0-691-11321-0。
• ベック、マティアス、ゲオゲガン、ロス（2010年）『証明の芸術：より深い数学のための基礎トレーニング』、ニューヨーク：シュプリンガー、ISBN 978-1-4419-7022-0。
• ボナ、ミクローシュ（2011年）、『組合せ論入門』（第3版）、ニュージャージー州：ワールドサイエンティフィック、ISBN 978-981-4335-23-2。
• ジョナサン・M・ボーウェイン著、ピーター・B・ボーウェイン著（1998年7月）『円周率とAGM：解析的数論と計算複雑性の研究』 、Wiley、 91～ 101ページ 、 ISBN 978-0-471-31515-5
• レマーマイヤー、フランツ（2000年）『相互法則：オイラーからアイゼンシュタインまで』、シュプリンガー・モノグラフズ・イン・マスマティクス、ニューヨーク：シュプリンガー、ISBN 978-3-540-66957-9。
• リヴィオ、マリオ(2003) [2002]、『黄金比：世界で最も驚くべき数ファイの物語』（初版ペーパーバック）、ニューヨーク：ブロードウェイ・ブックス、ISBN 0-7679-0816-3
• リュカス、エドゥアール（1891年）『名詞の理論』（フランス語）、第1巻、パリ：ゴーティエ＝ヴィラール。
• Sigler, LE (2002)、『フィボナッチの算盤：レオナルド・ピサーノの計算書の現代英語への翻訳』、数学と物理科学の歴史における資料と研究、Springer、ISBN 978-0-387-95419-6

外部リンク

• フィボナッチ数列と黄金比：現代世界の数学 - YouTubeで- 数列、螺旋、黄金比、ウサギのつがいの成長を描いたアニメーション。美術、音楽、建築、自然、天文学における例
• MathPages のフィボナッチ数列の周期（Mod m）
• 科学者たちは自然界におけるフィボナッチ螺旋の形成の手がかりを発見した
• BBCの「In Our Time」におけるフィボナッチ数列
• 「フィボナッチ数列」、数学百科事典、EMSプレス、2001 [1994]