エマニュエル・ロデウィク・エルテ

エマヌエル・ロデウェイク・エルテ（1881年3月16日アムステルダム生まれ- 1943年4月9日ソビボル没）^{[ 1 ]}はオランダの数学者である。彼は4次元以上の半正多面体の発見と分類で知られる。

エルテの父ハルトグ・エルテはアムステルダムの学校の校長だった。エマヌエル・エルテは1912年、アムステルダムの高校教師として働いていた際にレベッカ・ストークと結婚した。1943年までに一家はハールレムに住んでいた。同年1月30日、ハールレムでドイツ人将校が銃撃され、報復としてエルテとその家族を含むハールレムの住民100人がフフト収容所に移送された。ユダヤ人であったため、エルテと妻はさらにソビボルに移送され、そこで殺害された。彼の2人の子供はアウシュビッツで殺害された。^{[ 1 ]}

エルテの第一種半正多面体

彼の研究は、ソロルド・ゴセットの有限半正則多面体を再発見し、さらに正則な面だけでなく、再帰的に1つまたは2つの半正則な面も許容するようになった。これらは、1912年の著書「超空間の半正則多面体」に列挙されている。^{[ 2 ]}彼は、それらを第一種の半正則多面体と呼び、探索を1つまたは2つのタイプの正則または半正則k面に限定した。これらの多面体とその他がコクセターによって再発見され、より大きなクラスである均一多面体の一部として改名された。^{[ 3 ]}その過程で、彼は、半正則性の彼の定義を満たさなかった142_{を除いて、例外的な E n}族の多面体の主な代表をすべて発見した。

第一種半正多面体の概要^{[ 4 ]}

n	エルテ記法	頂点	エッジ	顔	細胞	ファセット	シュレーフリ記号	コクセターシンボル	コクセター図
多面体（アルキメデスの立体）
3	tT	12	18	4p 3 +4p 6			t{3,3}
	tC	24	36	6p 8 +8p 3			t{4,3}
	に	24	36	6p 4 +8p 6			t{3,4}
	tD	60	90	20p 3 +12p 10			t{5,3}
	私	60	90	20p 6 +12p 5			t{3,5}
	TT = O	6	12	(4+4)p 3			r{3,3} = {3 ^1,1 }	0 11
	二酸化炭素	12	24	6p 4 +8p 3			r{3,4}
	ID	30	60	20p 3 +12p 5			r{3,5}
	P q	2q	4q	2p q +qp 4			t{2,q}
	AP q	2q	4q	2p q +2qp 3			s{2,2q}
半正則4次元多面体
4	tC 5	10	30	(10+20)p 3	5O+5T		r{3,3,3} = {3 ^2,1 }	0 21
	tC 8	32	96	64p 3 +24p 4	8CO+16T		r{4,3,3}
	tC 16 =C 24 (*)	48	96	96ページ3ページ	(16+8)O		r{3,3,4}
	tC 24	96	288	96ページ3 + 144ページ4	24 CO + 24 C		r{3,4,3}
	tC 600	720	3600	（1200 + 2400 ）p3	600O + 120 I		r{3,3,5}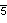
	tC 120	1200	3600	2400 p 3 + 720 p 5	120ID+600T		r{5,3,3}
	HM 4 = C 16 (*)	8	24	32ページ3	(8+8)T		{3,3 ^1,1 }	1 11
	–	30	60	20ページ3ページ+ 20ページ6ページ	（5 + 5）tT		2 t {3,3,3}
	–	288	576	192ページ3 + 144ページ8	（24 + 24）tC		2 t {3,4,3}
	–	20	60	40ページ3ページ+ 30ページ4ページ	10 T + 20 P 3		t 0,3 {3,3,3}
	–	144	576	384ページ3 + 288ペ​​ージ4	48O + 192 P 3		t 0,3 {3,4,3}
	–	問^2	2問^2	q ^2p 4 + 2 qp q	（q + q）P q		2t{ q ,2, q }
半正則5次元多面体
5	S 5 ^1	15	60	(20+60)p 3	30T+15O	6C 5 +6tC 5	r{3,3,3,3} = {3 ^3,1 }	0 31
	S 5 ^2	20	90	120p 3	30T+30O	(6+6)C 5	2r{3,3,3,3} = {3 ^2,2 }	0 22
	HM5​	16	80	160p 3	(80+40)T	16℃ 5 +10℃ 16	{3,3 ^2,1 }	1 21
	Cr 5 ^1	40	240	(80+320)p 3	160T+80O	32℃ 5 +10℃ 16	r{3,3,3,4}
	Cr 5 ^2	80	480	(320+320)p 3	80T+200O	32℃ 5 +10℃ 24	2r{3,3,3,4}
半正6次元多面体
6	S 6 ^1 (*)						r{3 ^5 } = {3 ^4,1 }	0 41
	S 6 ^2 (*)						2r{3 ^5 } = {3 ^3,2 }	0 32
	HM 6	32	240	640p 3	(160+480)T	32S 5 +12HM 5	{3,3 ^3,1 }	1 31
	V 27	27	216	720p 3	1080T	72S 5 +27HM 5	{3,3,3 ^2,1 }	2 21
	V 72	72	720	2160p 3	2160T	(27+27)HM 6	{3,3 ^2,2 }	1 22
半正7次元多面体
7	S 7 ^1 (*)						r{3 ^6 } = {3 ^5,1 }	0 51
	S 7 ^2 (*)						2r{3 ^6 } = {3 ^4,2 }	0 42
	S 7 ^3 (*)						3r{3 ^6 } = {3 ^3,3 }	0 33
	HM 7（*）	64	672	2240p 3	(560+2240)T	64S 6 +14HM 6	{3,3 ^4,1 }	1 41
	V 56	56	756	4032ページ3	10080T	576S 6 +126Cr 6	{3,3,3,3 ^2,1 }	3月21日
	V 126	126	2016	10080p 3	20160T	576S 6 +56V 27	{3,3,3 ^3,1 }	2 31
	V 576	576	10080	40320p 3	(30240+20160)T	126HM 6 +56V 72	{3,3 ^3,2 }	1 32
半正則8次元多面体
8	S 8 ^1 (*)						r{3 ^7 } = {3 ^6,1 }	0 61
	S 8 ^2 (*)						2r{3 ^7 } = {3 ^5,2 }	0 52
	S 8 ^3 (*)						3r{3 ^7 } = {3 ^4,3 }	0 43
	HM8 （ *）	128	1792	7168ページ3ページ	(1792+8960)T	128S 7 +16HM 7	{3,3 ^5,1 }	1 51
	V 2160	2160	69120	483840p 3	1209600T	17280S 7 +240V 126	{3,3,3 ^4,1 }	2 41
	V 240	240	6720	60480p 3	241920T	17280S 7 +2160Cr 7	{3,3,3,3,3 ^2,1 }	4 21

(*) この表ではエルテが認識したが明示的に列挙しなかったシーケンスとして追加されました

通常の次元ファミリー:

• S _n = n -単体: S ₃、S ₄、S ₅、S ₆、S ₇、S ₈、...
• M _n = n -立方体= 測定多面体: M ₃​​ 、M ₄、M ₅、M ₆、M ₇、M ₈、...
• HM _n = n -デミキューブ= 半分の測定多面体: HM ₃、HM ₄、M ₅、M ₆、HM ₇、HM ₈、...
• Cr _n = n -正多面体= 交差多面体: Cr ₃、Cr ₄、Cr ₅、Cr ₆、Cr ₇、Cr ₈、...

一次半正多面体:

• V _n = n頂点の半正多面体

ポリゴン

• P _n =正n角形

多面体:

• レギュラー: T、C、O、I、D
• 切り捨て: tT、tC、tO、tI、tD
• 準規則（整流）：CO、ID
• 認証: RCO、RID
• 切断準正規配列（オムニトランケーテッド配列）：tCO、tID
• プリズマティック: P _n、AP _n

4次元多面体:

• C _n = n個のセルを持つ正4次元多面体: C ₅、C ₈、C ₁₆、C ₂₄、C ₁₂₀、C ₆₀₀
• 整流: tC ₅、tC ₈、tC ₁₆、tC ₂₄、tC ₁₂₀、tC ₆₀₀

参照

• ゴセット・エルテ図

注記

1. Emanuël Lodewijk Elte Archived 2013-12-13 at the Wayback Machine at joodsmonument.nl
2. Elte、EL (1912)、超空間の半規則多面体、フローニンゲン: フローニンゲン大学、ISBN 1-4181-7968-X[1] [2]
3. Coxeter, HSM Regular polytopes , 3rd Edn, Dover (1973) p. 210 (11.x 歴史的注釈)
4. 128ページ