フラットモジュール

代数学において、平坦加群には自由加群、射影加群、そして主イデアル領域上の捩れのない加群が含まれる。正式には、環R上の加群Mが平坦であるとは、RとMのテンソル積が正確な列を保存することを意味する。加群が忠実に平坦であるとは、列とのテンソル積が正確な列を生成することと、元の列が正確であることとが同値であることを意味する。

平坦性は、 Jean-Pierre Serre  ( 1956 ) の論文「Géometrie Algébrique et Géométrie Analytique」で導入されました。

意味

環R上の左加群Mが平坦であるとは、次の条件が満たされる場合である:右R加群の任意の入射線型写像に対して、写像 ${\displaystyle \varphi :K\to L}$

${\displaystyle \varphi \otimes _{R}M:K\otimes _{R}M\to L\otimes _{R}M}$

も単射であり、ここで誘導される写像は${\displaystyle \varphi \otimes _{R}M}$ ${\displaystyle k\otimes m\mapsto \varphi (k)\otimes m.}$

この定義では、 Rへの有限生成イデアルの包含への注入を制限すれば十分です。 ${\displaystyle \varphi }$

同様に、R加群Mが平坦であるとは、Mとのテンソル積が完全関数である場合、つまり、R加群のすべての短完全列に対して、その列も完全である場合です。(テンソル積は右完全関数であるため、これは同等の定義です。) ${\displaystyle 0\rightarrow K\rightarrow L\rightarrow J\rightarrow 0,}$ ${\displaystyle 0\rightarrow K\otimes _{R}M\rightarrow L\otimes _{R}M\rightarrow J\otimes _{R}M\rightarrow 0}$

これらの定義は、 Rが非可換環で、Mが左R加群の場合にも適用されます。この場合、K、L、およびJ は右R加群でなければならず、テンソル積は一般にR加群ではなく、アーベル群のみです。

特徴づけ

平坦性は次の等式条件によって特徴付けることもできます。これは、 MのR -線形関係がRの線形関係から生じることを意味します。

左R加群Mが平坦であることと、任意の線形関係に対して

${\textstyle \sum _{i=1}^{m}r_{i}x_{i}=0}$

および のとき、となる元および が存在する。 ^{[ 1 ]}${\displaystyle r_{i}\in R}$ ${\displaystyle x_{i}\in M}$ ${\displaystyle y_{j}\in M}$ ${\displaystyle a_{i,j}\in R,}$

${\textstyle \sum _{i=1}^{m}r_{i}a_{i,j}=0\qquad }$ のために${\displaystyle j=1,\ldots ,n,}$

そして

${\textstyle x_{i}=\sum _{j=1}^{n}a_{i,j}y_{j}\qquad }$ のために${\displaystyle i=1,\ldots ,m.}$

これは、加群のn個の元と、この加群への線型写像（これはの標準基底をn個の元に写す）を定義することと同値である。これにより、前述の特徴付けを準同型写像を用いて以下のように書き直すことができる。 ${\displaystyle R^{n}}$ ${\displaystyle R^{n}}$

R 加群Mが平坦であるための必要十分条件は、次の条件が成り立つことである: が有限生成自由 R 加群であるすべての写像に対して、写像の有限生成R部分加群は写像gを介して自由R加群に因数分解され、${\displaystyle f:F\to M,}$ ${\displaystyle F}$ ${\displaystyle K}$ ${\displaystyle \ker f,}$ ${\displaystyle f}$ ${\displaystyle G}$ ${\displaystyle g(K)=0:}$

平坦モジ​​ュールの因子特性

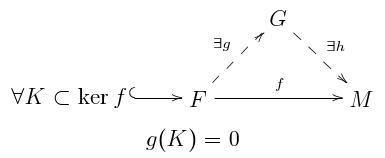
他のモジュールプロパティとの関係

平坦性は、自由、射影、捩れなしといった様々な加群の性質と関連しています。特に、すべての平坦加群は捩れなし、すべての射影加群は平坦、すべての自由加群は射影です。

平坦かつ射影的でない有限生成加群も存在します。しかし、平坦な有限生成加群はすべて、最も一般的に考えられる環上に射影的です。さらに、有限生成加群が平坦であるためには、局所自由であることが必要です。つまり、素イデアルにおけるすべての局所化は自由加群であるということです。

これは次の図に部分的にまとめられています。

可換代数におけるモジュールの性質

ねじれのないモジュール

すべての平坦加群はねじれを生じない。これは、 m = 1とした場合の上記の関係式による特徴付けから得られる。

逆は整数に対しても成り立ち、より一般的には主イデアル領域とデデキント環に対しても成り立ちます。

すべてのねじれのないモジュールが平坦である積分領域は、プリューファー領域と呼ばれます。

自由モジュールと射影モジュール

モジュールMが射影的である場合、かつその場合のみ、自由モジュールGと 2 つの線型写像が存在し、 となります。特に、すべての自由モジュールは射影的です ( および を取ります) 。${\displaystyle i:M\to G}$ ${\displaystyle p:G\to M}$ ${\displaystyle p\circ i=\mathrm {id} _{M}.}$ ${\displaystyle G=M}$ ${\displaystyle i=p=\mathrm {id} _{M}}$

すべての射影加群は平坦である。これは、線形写像による平坦性と射影性の上記の特徴づけから、次のように証明できる。${\displaystyle g=i\circ f}$ ${\displaystyle h=p.}$

逆に、有限生成平坦加群は、可換代数と代数幾何学において一般的に満たされる緩やかな条件の下で射影的である。そのため、平坦性の概念は主に有限生成ではない加群に対して有用である。

平坦な有限生成加群（有限生成自由加群を有限生成部分加群で割ったもの）は常に射影的である。これは、f を射影的とし、上記の線型写像による平坦性の特徴付けによって証明できる。この条件は、線型写像が存在し、したがって となることを意味する。fが射影的であるならば、したがって となり、Mは射影的である。 ${\displaystyle K=\ker f}$ ${\displaystyle g(K)=0}$ ${\displaystyle i:M\to G}$ ${\displaystyle i\circ f=g,}$ ${\displaystyle h\circ i\circ f=h\circ g=f.}$ ${\displaystyle h\circ i=\mathrm {id} _{M},}$

ネーター環上において、すべての有限生成平坦加群は射影的である。これは、すべての有限生成加群が有限表示されるからである。整域上においても、たとえネーター環でなくても、同様の結果が成り立つ。 ^{[ 2 ]}

局所環上では、すべての有限生成平坦モジュールは自由である。^{[ 3 ]}

射影的でない有限生成平坦加群は、以下のように構築できる。固定体Fに属する項を持つ無限列全体の集合を とする。これは可換環であり、成分ごとに加法と乗法が定義されている。この環は絶対平坦（つまり、すべての加群が平坦）である。Iが有限個の非零項を持つ列のイデアルである加群は、平坦かつ有限生成（生成元は1つだけ）であるが、射影的ではない。 ${\displaystyle R=F^{\mathbb {N} }}$ ${\displaystyle R/I,}$

非例

• I がノイザン可換環Rのイデアルである場合、 は平坦加群ではない。ただし、I が冪等元（つまり、その平方に等しい元）によって生成される場合は除く。特に、Rが整域である場合、 が平坦となるのは、がR に等しいか、 が零イデアルである場合のみである。${\displaystyle R/I}$ ${\displaystyle R/I}$ ${\displaystyle I}$
• 整域上では、平坦加群は捩れ係数を持たない。したがって、捩れ係数が零でない元を含む加群は平坦ではない。特に、正特性体およびすべての正特性体は非平坦 -加群である。ここで、 は整数環、 は有理数体である。${\displaystyle \mathbb {Q} /\mathbb {Z} }$ ${\displaystyle \mathbb {Z} }$ ${\displaystyle \mathbb {Z} }$ ${\displaystyle \mathbb {Q} }$

直和、極限、積

モジュールの直和が フラットになるのは、各モジュールがフラットである場合のみです。 ${\displaystyle \textstyle \bigoplus _{i\in I}M_{i}}$ ${\displaystyle M_{i}}$

平坦加群の直極限は平坦である。特に、自由加群の直極限は平坦である。逆に、すべての平坦加群は有限生成自由加群の直極限として書くことができる。^{[ 4 ]}

平坦加群の直積は一般に平坦である必要はない。実際、環Rが与えられたとき、平坦R加群のすべての直積が平坦となるのは、 R が連接環である場合（すなわち、すべての有限生成イデアルが有限提示される場合）に限ります。^{[ 5 ]}

フラットリングエクステンション

環準同型が平坦であるとは、 S がその準同型によって誘導される加群構造に対して平坦R加群となることである。例えば、任意の環Rに対して、多項式環R [ t ]はR上平坦である。 ${\displaystyle R\to S}$

可換環の任意の乗法部分集合 に対して、局所化は平坦R代数である（例外的な場合にのみ射影的となる）。例えば、は平坦であり、 に対しては射影的ではない。${\displaystyle S}$ ${\displaystyle R}$ ${\displaystyle S^{-1}R}$ ${\displaystyle \mathbb {Q} }$ ${\displaystyle \mathbb {Z} .}$

がノイザン可換環のイデアルであるとき、 の に関する完備化は平坦である。^{[ 6 ]}が忠実に平坦であるための必要十分条件は、が のヤコブソン根基に含まれることである（ザリスキー環も参照）。^{[ 7 ]}${\displaystyle I}$ ${\displaystyle R,}$ ${\displaystyle {\widehat {R}}}$ ${\displaystyle R}$ ${\displaystyle I}$ ${\displaystyle I}$ ${\displaystyle A.}$

ローカルプロパティ

この節では、R は可換環を表す。Rの素イデアルがRである場合、における局所化は、通常通り、 を添え字として表される。すなわち、MがR加群である場合、${\displaystyle {\mathfrak {p}}}$ ${\displaystyle {\mathfrak {p}}}$ ${\displaystyle {\mathfrak {p}}}$ ${\displaystyle R_{\mathfrak {p}}=(R\setminus {\mathfrak {p}})^{-1}R,}$ ${\displaystyle M_{\mathfrak {p}}=(R\setminus {\mathfrak {p}})^{-1}M=R_{\mathfrak {p}}\otimes _{R}M.}$

MがRモジュールである場合、次の 3 つの条件は同等です。

• ${\displaystyle M}$ はフラットな- 加群である。${\displaystyle R}$
• ${\displaystyle M_{\mathfrak {p}}}$ はすべての素イデアルに対して平坦な -加群である${\displaystyle R_{\mathfrak {p}}}$ ${\displaystyle {\mathfrak {p}};}$
• ${\displaystyle M_{\mathfrak {m}}}$ はあらゆる極大イデアルに対して平坦な -加群である${\displaystyle R_{\mathfrak {m}}}$ ${\displaystyle {\mathfrak {m}}.}$

この性質は可換代数と代数幾何学において基本的なものであり、平坦性の研究を局所環の場合に還元するものである。これらはしばしば、平坦性は局所的性質であると表現される。

スキームの平坦射

スキームの平坦射の定義は、平坦性の局所的特性から直接生じます。

スキームの射が平坦射であるとは、局所環上の誘導写像 が${\displaystyle f:X\to Y}$

${\displaystyle {\mathcal {O}}_{Y,f(x)}\to {\mathcal {O}}_{X,x}}$

は、 X内の任意の点xに対する平坦環準同型です。

したがって、平坦な（または忠実に平坦な）環準同型の性質は、代数幾何学における平坦射の幾何学的性質に自然に拡張されます。

例えば、平坦代数（下記参照）を考えてみましょう。包含関係により平坦射が誘導されます。 ${\displaystyle \mathbb {C} [t]}$ ${\displaystyle R=\mathbb {C} [t,x,y]/(xy-t)}$ ${\displaystyle \mathbb {C} [t]\hookrightarrow R}$

${\displaystyle \pi :\operatorname {Spec} (R)\to \operatorname {Spec} (\mathbb {C} [t]).}$

(幾何学的) ファイバーは、次の式で与えられる曲線です(平坦な変性と通常の円錐への変形も参照)。 ${\displaystyle \pi ^{-1}(t)}$ ${\displaystyle xy=t.}$

を可換ノイザン環と非零因子上の多項式環とする。このとき、が 上平坦であることと、が原始的であること（係数が単位イデアルを生成すること）は同値である。^{[ 8 ]}例として^{[ 9 ]}があり、これは 上平坦（かつ自由）である（幾何学的な意味については下記も参照）。このような平坦拡大は、自由ではなく局所化から生じない平坦加群の例を生成するために用いることができる。 ${\displaystyle S=R[x_{1},\dots ,x_{r}]}$ ${\displaystyle R}$ ${\displaystyle f\in S}$ ${\displaystyle S/fS}$ ${\displaystyle R}$ ${\displaystyle f}$ ${\displaystyle \mathbb {C} [t,x,y]/(xy-t),}$ ${\displaystyle \mathbb {C} [t]}$

忠実な平坦さ

加群が忠実平坦であるとは、数列とのテンソル積が正確な数列を生成することと、元の数列が正確であることとが同値であることを意味する。この概念は非可換環上の加群に対して定義されているが、主に可換環に対して用いられる。したがって、いくつかの結果は非可換環上の加群の場合にも一般化できるものの、ここではこのケースのみを考察する。

この節では、は可換環の環準同型であり、 -代数と-加群の構造を与える。が -加群平坦（または忠実平坦）である場合、一般に はに対して平坦（または忠実平坦）であり、 はに対して平坦（または忠実平坦）であると言われる。 ${\displaystyle f\colon R\to S}$ ${\displaystyle S}$ ${\displaystyle R}$ ${\displaystyle R}$ ${\displaystyle S}$ ${\displaystyle R}$ ${\displaystyle S}$ ${\displaystyle R,}$ ${\displaystyle f}$

が平坦である場合、以下の条件は同等です。 ${\displaystyle S}$ ${\displaystyle R,}$

• ${\displaystyle S}$ 忠実にフラットです。
• の各最大イデアルに対して、${\displaystyle {\mathfrak {m}}}$ ${\displaystyle R}$ ${\displaystyle {\mathfrak {m}}S\neq S.}$
• が非ゼロの -モジュールである場合、${\displaystyle M}$ ${\displaystyle R}$ ${\displaystyle M\otimes _{R}S\neq 0.}$
• のすべての素イデアルに対して、となる素イデアルが存在する。言い換えると、によってスペクトル上に誘導される写像は射影的である。${\displaystyle {\mathfrak {p}}}$ ${\displaystyle R,}$ ${\displaystyle {\mathfrak {P}}}$ ${\displaystyle S}$ ${\displaystyle {\mathfrak {p}}=f^{-1}({\mathfrak {P}}).}$ ${\displaystyle f^{*}\colon \operatorname {Spec} (S)\to \operatorname {Spec} (R)}$ ${\displaystyle f}$
• ${\displaystyle f,}$ は単射であり、の純粋部分環、すなわち任意の- 加群に対して単射である。^{[ a ]}${\displaystyle R}$ ${\displaystyle S;}$ ${\displaystyle M\to M\otimes _{R}S}$ ${\displaystyle R}$ ${\displaystyle M}$

2番目の条件は、局所環の平坦局所準同型が忠実平坦であることを意味する。最後の条件から、 ( を取る)の任意のイデアルに対してが成り立つ。特に、がネーター環であるならば、もネーター環となる。 ${\displaystyle I=IS\cap R}$ ${\displaystyle I}$ ${\displaystyle R}$ ${\displaystyle M=R/I}$ ${\displaystyle S}$ ${\displaystyle R}$

最後から2番目の条件は、次のように強化された形で述べることができます。は沈み込み的であり、これは のザリスキー位相が のザリスキー位相の商位相であることを意味します（これは、スキームの忠実に平坦な準コンパクト射がこの性質を持つという事実の特別な場合です。^{[ 10 ]}）。平坦射の§平坦射の性質も参照してください。 ${\displaystyle \operatorname {Spec} (S)\to \operatorname {Spec} (R)}$ ${\displaystyle \operatorname {Spec} (R)}$ ${\displaystyle \operatorname {Spec} (S)}$

例

• 非零自由R加群となるような環準同型は忠実平坦である。例えば、 ${\displaystyle R\to S}$ ${\displaystyle S}$
  • あらゆる体拡大は忠実に平坦である。この性質は、実ベクトル空間における結果の証明に複素化を用いることの背後に暗黙的に存在している。
  • 多項式環は、その係数の環を忠実に平坦に拡張したものです。
  • が単項多項式である場合、包含は忠実に平坦です。${\displaystyle p\in R[x]}$ ${\displaystyle R\hookrightarrow R[t]/\langle p\rangle }$
• とすると、における局在の直積が上で忠実に平坦であることと、の単位イデアルが を生成することが等しい（つまり、が の線型結合である場合）。^{[ 11 ]}${\displaystyle t_{1},\ldots ,t_{k}\in R.}$ ${\displaystyle \textstyle \prod _{i}R[t_{i}^{-1}]}$ ${\displaystyle t_{i}}$ ${\displaystyle R}$ ${\displaystyle t_{1},\ldots ,t_{k}}$ ${\displaystyle R}$ ${\displaystyle 1}$ ${\displaystyle t_{i}}$
• すべての素イデアルの局所化の直和は、素イデアルが有限個ある場合を除いて、代数ではない忠実に平坦なモジュールです。${\displaystyle R_{\mathfrak {p}}}$ ${\displaystyle R}$

最後の 2 つの例は、可換代数と代数幾何学における局所化の広範な使用の背後に暗黙的に存在します。

• 与えられた環準同型に対して、アミチュール複体と呼ばれる複体が存在する: ^{[ 12 ]}${\displaystyle f:A\to B,}$

$${\displaystyle 0\to A{\overset {f}{\to }}B{\overset {\delta ^{0}}{\to }}B\otimes _{A}B{\overset {\delta ^{1}}{\to }}B\otimes _{A}B\otimes _{A}B\to \cdots }$$ ここで、共境界演算子は、各点に1を挿入することによって得られる写像の交代和です。例えば、。そして、(グロタンディーク) が忠実に平坦であれば、この複体は正確です。 ${\displaystyle \delta ^{n}}$ ${\displaystyle \delta ^{0}(b)=b\otimes 1-1\otimes b}$ ${\displaystyle f}$

忠実に平坦な局所準同型

ここに、必ずしも平坦ではない準同型に対する忠実平坦準同型の一つの特徴付けを示す。が-主イデアルであるような入射的局所準同型が与えられたとき、その準同型が忠実平坦であるための必要十分条件は、遷移定理が成り立つことである。すなわち、の各- 主イデアルに対して、^{[ 13 ]}${\displaystyle (R,{\mathfrak {m}})\hookrightarrow (S,{\mathfrak {n}})}$ ${\displaystyle {\mathfrak {m}}S}$ ${\displaystyle {\mathfrak {n}}}$ ${\displaystyle S\to B}$ ${\displaystyle {\mathfrak {m}}}$ ${\displaystyle {\mathfrak {q}}}$ ${\displaystyle R}$ ${\displaystyle \operatorname {length} _{S}(S/{\mathfrak {q}}S)=\operatorname {length} _{S}(S/{\mathfrak {m}}S)\operatorname {length} _{R}(R/{\mathfrak {q}}).}$

Tor関数を用いたホモロジー的特徴付け

平坦性は、テンソル積の左導来関手であるTor関手を用いて表現することもできる。左-加群が平坦であるための必要十分条件は、 ${\displaystyle R}$ ${\displaystyle M}$

${\displaystyle \operatorname {Tor} _{n}^{R}(X,M)=0}$ すべての右モジュールについて）。^{[ b ]}${\displaystyle n\geq 1}$ ${\displaystyle R}$ ${\displaystyle X}$

実際、最初のTor項が消えること、つまりMが平坦であるのは

${\displaystyle \operatorname {Tor} _{1}^{R}(N,M)=0}$

任意の- 加群に対して、あるいはさらに限定的に、および が任意の有限生成イデアルである場合に、 となります。 ${\displaystyle R}$ ${\displaystyle N}$ ${\displaystyle N=R/I}$ ${\displaystyle I\subset R}$

Tor関数の長完全列を使うと、短完全列に関する事実を簡単に証明できる。

${\displaystyle 0\to A{\overset {f}{\longrightarrow }}B{\overset {g}{\longrightarrow }}C\to 0}$

と が平坦であれば、 も平坦です。また、と が平坦であれば、 も平坦です。と が平坦であれば、 は一般に平坦である必要はありません。ただし、がにおいて純粋でが平坦であれば、とは平坦です。 ${\displaystyle A}$ ${\displaystyle C}$ ${\displaystyle B}$ ${\displaystyle B}$ ${\displaystyle C}$ ${\displaystyle A}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle C}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle B}$ ${\displaystyle A}$ ${\displaystyle C}$

フラット解像度

モジュールのフラットな解決とは、次のような形式の 解決である。${\displaystyle M}$

${\displaystyle \cdots \to F_{2}\to F_{1}\to F_{0}\to M\to 0,}$

ここで、はすべて平坦な加群です。任意の自由または射影的な解決は必ず平坦な解決になります。平坦な解決はTor関手を計算するために使用できます。 ${\displaystyle F_{i}}$

有限平坦解像度の長さは、が非ゼロでに対してとなるような最初の添え字nです。モジュールが有限平坦解像度を許容する場合、 のすべての有限平坦解像度の中で最小の長さはその平坦次元^{[ 14 ]}と呼ばれ、 と表記されます。が有限平坦解像度を許容しない場合は、慣例により平坦次元は無限であるということになります。例として、となるモジュールを考えてみましょう。この状況では、シーケンスの正確さから、中央の矢印は同型であり、したがってそれ自体が平坦であることがわかります。^{[ c ]}${\displaystyle F_{n}}$ ${\displaystyle F_{i}=0}$ ${\displaystyle i>n}$ ${\displaystyle M}$ ${\displaystyle M}$ ${\displaystyle \operatorname {fd} (M)}$ ${\displaystyle M}$ ${\displaystyle M}$ ${\displaystyle \operatorname {fd} (M)=0}$ ${\displaystyle 0\to F_{0}\to M\to 0}$ ${\displaystyle M}$

加群理論の一部の分野では、平坦分解は、各写像が右写像の核の平坦前被覆であるという追加要件を満たす必要がある。射影分解の場合、この条件はほとんど目に見えない。射影前被覆は、単に射影加群からの射影写像である。これらのアイデアは、アウスランダーの近似に関する研究に着想を得たものである。また、これらのアイデアは、各写像が右写像の核の射影被覆であることが求められる、より一般的な概念である極小射影分解からも知られている。しかし、射影被覆は一般には存在する必要がないため、極小射影分解は整数環のような環上でのみ限定的に用いられる。

フラットカバー

加群の射影被覆は常に存在するわけではないが、一般の環に対しては、すべての加群が平坦被覆を持つ、つまりすべての加群Mが平坦加群Fのエピモーフィック像となり、平坦加群からMへのすべての写像がFを通り、FのM上への任意の自己準同型が自己同型になるという予想がなされた。この平坦被覆予想は、 Enochs ( 1981 、p. 196)で初めて明示的に述べられた。この予想は真であることが判明し、L. Bican、R. El Bashir、E. Enochs によって同時に肯定的に解決され、証明された。^{[ 15 ]}これに先立って、P. Eklof、J. Trlifaj、J. Xu による重要な貢献があった。

すべての環上のすべての加群に対して平坦被覆が存在するため、多くの状況において、極小平坦分解は極小射影分解に取って代わることができる。平坦分解の射影分解からの乖離の測定は相対ホモロジー代数と呼ばれ、Mac Lane ( 1963 )などの古典的研究や、Enochs and Jenda ( 2000 )などの平坦分解に焦点を当てた最近の研究で扱われている。

構成的数学において

平坦加群は、射影加群があまり有用でない構成数学において重要性を増している。例えば、すべての自由加群が射影的であることは選択公理の完全形と同値であるため、射影加群に関する定理は、たとえ構成的に証明されたとしても、必ずしも自由加群に適用できるわけではない。対照的に、自由加群が平坦であることを証明するためには選択は必要ないため、平坦加群に関する定理は依然として適用可能である。^{[ 16 ]}

参照

• 一般的な平坦性
• 平坦射影
• フォン ノイマン正則リング–すべてのモジュールが平坦になるリング。
• 通常は平らなリング

注記

1. 証明： が忠実平坦であるとする。R 加群に対しては写像は純部分環となり、したがって単射となる。したがって、は単射となる。逆に、が 上の加群である場合${\displaystyle f:R\to S}$ ${\displaystyle M,}$ ${\displaystyle S=R\otimes _{R}S\to S\otimes _{R}S}$ ${\displaystyle S}$ ${\displaystyle M\otimes _{R}S\to M\otimes _{R}(S\otimes S)\simeq (M\otimes _{R}S)\otimes _{R}S}$ ${\displaystyle M\to M\otimes _{R}S}$ ${\displaystyle M\neq 0}$ ${\displaystyle R}$ ${\displaystyle 0\neq M\subset M\otimes _{R}S.}$
2. 同様に、右- 加群が平坦であるためには、とすべての左 -加群に対して が。${\displaystyle R}$ ${\displaystyle M}$ ${\displaystyle \operatorname {Tor} _{n}^{R}(M,X)=0}$ ${\displaystyle n\geq 1}$ ${\displaystyle R}$ ${\displaystyle X}$
3. フラット モジュールと同型のモジュールは当然フラットです。

引用

1. ブルバキ、第1章、§2. 命題13、系1
2. カルティエ 1958 , Lemme 5, p. 249
3. 松村 1986、定理7.10
4. ラザード 1969
5. チェイス 1960
6. 松村 1970、定理55の系1、p.170
7. 松村 1970、定理56
8. アイゼンバッド 1995、演習6.4
9. アルティン、3ページ
10. SGA I、Exposé VIII.、Corollay 4.3
11. Artin 1999、命題III.5.2の後の演習(3)
12. 「アミトゥール・コンプレックス」ncatlab.org .
13. 松村 1986、第8章、演習22.1
14. ラム 1999、183ページ
15. ビカン、エル・バシル、エノクス 2001
16. リッチマン 1997

参考文献

• アルティン「変形理論」（PDF）。2019年11月18日時点のオリジナルよりアーカイブ（PDF） 。
• アルティン、マイケル(1999). 「非可換環」(PDF) .
• Bican, L.; El Bashir, R.; Enochs, E. (2001)「すべてのモジュールはフラットカバーを備えている」Bull. London Math. Soc. , 33 (4): 385– 390, doi : 10.1017/S0024609301008104 , ISSN  0024-6093 , MR  1832549
• カルティエ、ピエール (1958)。「幾何学の合理性に関する質問」。Bulletin de la Société Mathématique de France (フランス語)。86 : 177–251 .土井: 10.24033/bsmf.1503。
• ブルバキ、ニコラ。可換代数。
• チェイス、スティーブン・U.（1960）「加群の直積」アメリカ数学会誌、97（3）：457-473、doi：10.2307/1993382、JSTOR  1993382、MR  0120260
• アイゼンバッド、デイヴィッド（1995）、可換代数、Graduate Texts in Mathematics、第150巻、ベルリン、ニューヨーク：Springer-Verlag、doi：10.1007 / 978-1-4612-5350-1、ISBN 978-0-387-94268-1、MR  1322960
• エノックス、エドガー E. (1981)、「単射および平坦被覆、包絡線およびレゾルベント」、イスラエル数学ジャーナル、39 (3): 189– 209、doi : 10.1007/BF02760849、ISSN  0021-2172、MR  0636889、S2CID  120567780
• イノクス、エドガー E. Jenda、Overtoun MG (2000)、相対ホモロジー代数、de Gruyter Expositions in Mathematics、vol. 30、ベルリン: Walter de Gruyter & Co.、土井: 10.1515/9783110803662、ISBN 978-3-11-016633-0、MR  1753146
• クンツ、エルンスト（1969）、「特性pの正則局所環の特徴づけ」、アメリカ数学誌、91（3）：772–784、doi：10.2307/2373351、JSTOR  2373351、MR  0252389
• Lam, Tsit-Yuen (1999), Lectures on modules and rings , Graduate Texts in Mathematics No. 189, vol. 189, Berlin, New York: Springer-Verlag , doi : 10.1007/978-1-4612-0525-8 , ISBN 978-0-387-98428-5、MR  1653294
• Lazard、Daniel (1969)、「Autour de la platitude」、Bulletin de la Société Mathématique de France、97 : 81–128、doi : 10.24033/bsmf.1675
• Mac Lane、Saunders (1963)、ホモロジー、Die Grundlehren der mathematischen Wissenschaften、Bd. 114、ボストン、マサチューセッツ州: Academic Press、MR  0156879
• 松村英之 (1970)、可換代数
• 松村秀之 (1986).可換環論. Cambridge Studies in Advanced Mathematics. 第8巻. Cambridge University Press. ISBN 0-521-36764-6。MR  0879273。Zbl  0603.13001。
• マンフォード、デイヴィッド、『変種とスキームの赤い本』
• Northcott, DG (1984),多重線型代数, Cambridge University Press , p. 33, ISBN 978-0-521-26269-9
• リッチマン、フレッド（1997）、「平坦次元、構成性、そしてヒルベルトのシジジー定理」、ニュージーランド数学ジャーナル、26（2）：263-273、ISSN  1171-6096、MR  1601663
• SGA 1、Exposé VIII – これが主な参考文献です（ただし、これはGiraud（1964）の結果に依存しており、これは（より一般的な形で）SGA1の未発表のExposé VIIに取って代わりました）
• Serre, Jean-Pierre (1956)、「幾何学的幾何学と幾何学的分析」、Annales de l'Institut Fourier、6 : 1–42、doi : 10.5802/aif.59、ISSN  0373-0956、MR  0082175