2 22 honeycomb

222 honeycomb
(no image)
Type	Uniform tessellation
Coxeter symbol	222
Schläfli symbol	{3,3,3^2,2}
Coxeter diagram
6-face type	221
5-face types	211{3^4}
4-face type	{3^3}
Cell type	{3,3}
Face type	{3}
Face figure	{3}×{3} duoprism
Edge figure	{3^2,2}
Vertex figure	122
Coxeter group	${\displaystyle {\tilde {E}}_{6}}$ , [[3,3,3^2,2]]
Properties	vertex-transitive, facet-transitive

In geometry, the 2₂₂ honeycomb is a uniform tessellation of the six-dimensional Euclidean space. It can be represented by the Schläfli symbol {3,3,3^2,2}. It is constructed from 2₂₁facets and has a 1₂₂vertex figure, with 54 2₂₁ polytopes around every vertex.

Its vertex arrangement is the E₆ lattice, and the root system of the E₆Lie group so it can also be called the E₆ honeycomb.

Construction

It is created by a Wythoff construction upon a set of 7 hyperplane mirrors in 6-dimensional space.

The facet information can be extracted from its Coxeter–Dynkin diagram, .

Removing a node on the end of one of the 2-node branches leaves the 2₂₁, its only facet type,

The vertex figure is determined by removing the ringed node and ringing the neighboring node. This makes 1₂₂, .

The edge figure is the vertex figure of the vertex figure, here being a birectified 5-simplex, t₂{3⁴}, .

The face figure is the vertex figure of the edge figure, here being a triangular duoprism, {3}×{3}, .

Kissing number

Each vertex of this tessellation is the center of a 5-sphere in the densest known packing in 6 dimensions, with kissing number 72, represented by the vertices of its vertex figure1₂₂.

E₆ lattice

The 2₂₂ honeycomb's vertex arrangement is called the E₆ lattice.^[1]

The E₆² lattice, with [[3,3,3^2,2]] symmetry, can be constructed by the union of two E₆ lattices:

∪

The E₆^* lattice^[2] (or E₆³) with [[3,3^2,2,2]] symmetry. The Voronoi cell of the E₆^* lattice is the rectified 1₂₂ polytope, and the Voronoi tessellation is a bitruncated 2₂₂ honeycomb.^[3] It is constructed by 3 copies of the E₆ lattice vertices, one from each of the three branches of the Coxeter diagram.

∪ ∪ = dual to .

Geometric folding

The ${\displaystyle {\tilde {E}}_{6}}$ group is related to the ${\displaystyle {\tilde {F}}_{4}}$ by a geometric folding, so this honeycomb can be projected into the 4-dimensional 16-cell honeycomb.

${\displaystyle {\tilde {E}}_{6}}$	${\displaystyle {\tilde {F}}_{4}}$
{3,3,3^2,2}	{3,3,4,3}

Related honeycombs

The 2₂₂ honeycomb is one of 127 uniform honeycombs (39 unique) with ${\displaystyle {\tilde {E}}_{6}}$ symmetry. 24 of them have doubled symmetry [[3,3,3^2,2]] with 2 equally ringed branches, and 7 have sextupled (3!) symmetry [[3,3^2,2,2]] with identical rings on all 3 branches. There are no regular honeycombs in the family since its Coxeter diagram a nonlinear graph, but the 2₂₂ and birectified 2₂₂ are isotopic, with only one type of facet: 2₂₁, and rectified 1₂₂ polytopes respectively.

Symmetry	Order	Honeycombs
[3^2,2,2]	Full	8: , , , , , , , .
[[3,3,3^2,2]]	×2	24: , , , , , , , , , , , , , , , , , , , , , , , .
[[3,3^2,2,2]]	×6	7: , , , , , , .

Birectified 2₂₂ honeycomb

Birectified 222 honeycomb
(no image)
Type	Uniform tessellation
Coxeter symbol	0222
Schläfli symbol	{3^2,2,2}
Coxeter diagram
6-face type	0221
5-face types	0220211
4-face type	02124-cell 0111
Cell type	Tetrahedron 020Octahedron 011
Face type	Triangle 010
Vertex figure	Proprism {3}×{3}×{3}
Coxeter group	6×${\displaystyle {\tilde {E}}_{6}}$ , [[3,3^2,2,2]]
Properties	vertex-transitive, facet-transitive

The birectified 2₂₂ honeycomb, has rectified 1 22 polytope facets, , and a proprism {3}×{3}×{3} vertex figure.

Its facets are centered on the vertex arrangement of E₆^* lattice, as:

∪ ∪

Construction

The facet information can be extracted from its Coxeter–Dynkin diagram, .

The vertex figure is determined by removing the ringed node and ringing the neighboring node. This makes a proprism {3}×{3}×{3}, .

Removing a node on the end of one of the 3-node branches leaves the rectified 1₂₂, its only facet type, .

Removing a second end node defines 2 types of 5-faces: birectified 5-simplex, 0₂₂ and birectified 5-orthoplex, 0₂₁₁.

Removing a third end node defines 2 types of 4-faces: rectified 5-cell, 0₂₁, and 24-cell, 0₁₁₁.

Removing a fourth end node defines 2 types of cells: octahedron, 0₁₁, and tetrahedron, 0₂₀.

k₂₂ polytopes

The 2₂₂ honeycomb, is fourth in a dimensional series of uniform polytopes, expressed by Coxeter as k₂₂ series. The final is a paracompact hyperbolic honeycomb, 3₂₂. Each progressive uniform polytope is constructed from the previous as its vertex figure.

k₂₂ figures in n dimensions

Space	Finite			Euclidean	Hyperbolic
n	4	5	6	7	8
Coxetergroup	A2A2	E6	${\displaystyle {\tilde {E}}_{6}}$ =E6^+	${\displaystyle {\bar {T}}_{7}}$ =E6^++
Coxeterdiagram
Symmetry	[[3^2,2,-1]]	[[3^2,2,0]]	[[3^2,2,1]]	[[3^2,2,2]]	[[3^2,2,3]]
Order	72	1440	103,680	∞
Graph				∞	∞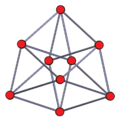
Name	−122	022	122	222	322

The 2₂₂ honeycomb is third in another dimensional series 2_2k.

2_2k figures of n dimensions

Space	Finite			Euclidean	Hyperbolic
n	4	5	6	7	8
Coxetergroup	A2A2	A5	E6	${\displaystyle {\tilde {E}}_{6}}$ =E6^+	E6^++
Coxeterdiagram
Graph				∞	∞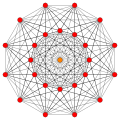
Name	22,-1	220	221	222	223

Notes

1. "The Lattice E6".
2. "The Lattice E6*".
3. The Voronoi Cells of the E6* and E7* LatticesArchived 2016-01-30 at the Wayback Machine, Edward Pervin

References

• CoxeterThe Beauty of Geometry: Twelve Essays, Dover Publications, 1999, ISBN 978-0-486-40919-1 (Chapter 3: Wythoff's Construction for Uniform Polytopes)
• CoxeterRegular Polytopes (1963), Macmillan Company
  • Regular Polytopes, Third edition, (1973), Dover edition, ISBN 0-486-61480-8 (Chapter 5: The Kaleidoscope)
• Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, wiley.com, ISBN 978-0-471-01003-6, GoogleBook
  • (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3–45]
• R. T. Worley, The Voronoi Region of E6*. J. Austral. Math. Soc. Ser. A, 43 (1987), 268–278.
• Conway, John H.; Sloane, Neil J. A. (1998). Sphere Packings, Lattices and Groups (3rd ed.). New York: Springer-Verlag. ISBN 0-387-98585-9. pp. 125–126, 8.3 The 6-dimensional lattices: E6 and E6*
• Klitzing, Richard. "6D Hexacombs x3o3o3o3o *c3o3o - jakoh".
• Klitzing, Richard. "6D Hexacombs o3o3x3o3o *c3o3o - ramoh".

v t e Fundamental convex regular and uniform honeycombs in dimensions 2–9
Space	Family	${\displaystyle {\tilde {A}}_{n-1}}$	${\displaystyle {\tilde {C}}_{n-1}}$	${\displaystyle {\tilde {B}}_{n-1}}$	${\displaystyle {\tilde {D}}_{n-1}}$	${\displaystyle {\tilde {G}}_{2}}$ / ${\displaystyle {\tilde {F}}_{4}}$ / ${\displaystyle {\tilde {E}}_{n-1}}$
E^2	Uniform tiling	0[3]	δ3	hδ3	qδ3	Hexagonal
E^3	Uniform convex honeycomb	0[4]	δ4	hδ4	qδ4
E^4	Uniform 4-honeycomb	0[5]	δ5	hδ5	qδ5	24-cell honeycomb
E^5	Uniform 5-honeycomb	0[6]	δ6	hδ6	qδ6
E^6	Uniform 6-honeycomb	0[7]	δ7	hδ7	qδ7	222
E^7	Uniform 7-honeycomb	0[8]	δ8	hδ8	qδ8	133 • 331
E^8	Uniform 8-honeycomb	0[9]	δ9	hδ9	qδ9	152 • 251 • 521
E^9	Uniform 9-honeycomb	0[10]	δ10	hδ10	qδ10
E^10	Uniform 10-honeycomb	0[11]	δ11	hδ11	qδ11
E^n−1	Uniform (n−1)-honeycomb	0[n]	δn	hδn	qδn	1k2 • 2k1 • k21