リッカート尺度
Psychometric measurement scale
Part of a series on
Sociology
Key themes
Perspectives
Branches
Methods
Major theorists

1800s: Martineau · Tocqueville · Marx · Spencer · Le Bon · Ward · Pareto · Tönnies · Veblen · Simmel · Durkheim · Addams · Mead · Weber · Du Bois · Mannheim · Elias

1900s: Fromm · Adorno · Gehlen · Aron · Merton · Nisbet · Mills · Bell · Schoeck · Goffman · Bauman · Foucault · Luhmann · Habermas · Baudrillard · Bourdieu · Giddens
Lists

リッカート尺度（/ ˈ l ɪ k ər t / LIK -ərt、[1] [注 1]）は、アメリカの社会心理学者レンシス・リッカート[ 2]にちなんで名付けられた心理測定尺度であり、調査質問票でよく用いられます。調査研究において回答を尺度化する手法として最も広く用いられており、この用語（またはより正確にはリッカート型尺度）は評価尺度と互換的に用いられることが多いものの、評価尺度には他にも様々な種類があります。

リッカートは、一連の項目（通常8項目以上）に対する集合的な回答から形成される尺度本体と、回答を範囲に沿って採点する形式を区別しました。厳密に言えば、リッカート尺度は前者のみを指します。[3] [4]この2つの概念の違いは、リッカートが調査対象となる根底にある現象と、根底にある現象を示す変動を捉える手段とを区別したことに関係しています。[5]

リッカート尺度に回答する際、回答者は一連の記述に対して、対称的な「賛成・反対」尺度を用いて同意または反対のレベルを指定します。したがって、その範囲は特定の項目に対する回答者の感情の強さを反映することになります。[6]

尺度は、個々の項目（質問）の集合に対するアンケート回答の単純な合計または平均として作成できます。その際、リッカート尺度法は、各選択肢（回答オプション）間の距離が等しいと仮定します。多くの研究者は、相関性が高く（高い内的一貫性を示す）、かつ全体として研究対象領域全体を網羅する（完全な相関関係には至らない）項目群を採用しています。また、「すべての項目は互いに複製されている、つまり並列的な尺度であると仮定する」という基準を支持する研究者もいます。[7] : 197 対照的に、現代のテスト理論では、各項目の難易度（ICC）は、項目の尺度作成に組み込むべき情報として扱われます。[8]

構成

ウェブサイトのデザインに関するアンケートの例（回答はリッカート尺度）

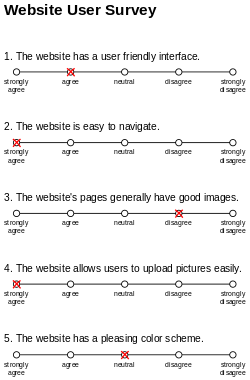
リッカート尺度は、複数のリッカート項目に対する回答の合計です。多くのリッカート尺度では、構成する各リッカート項目が、それぞれ独自の視覚的アナログ尺度（例えば、被験者が丸で囲んだりチェックマークを付けたりすることで回答を示す水平線）と対比されているため、個々の項目自体が尺度である、あるいは尺度を持つと誤って解釈されることがあり、この誤りが、この分野の文献や用語において蔓延する混乱を引き起こしています。

リッカート尺度項目とは、被調査者が主観的または客観的な尺度に基づいて定量的な値を与えることで評価を求められる記述であり、同意/不同意の程度が最も一般的に用いられる尺度です。適切に設計されたリッカート尺度項目は、「対称性」と「バランス」の両方を備えています。対称性とは、肯定的な立場と否定的な立場が同数含まれ、それぞれの距離が「中立」/ゼロ値（その値が候補として提示されているかどうかに関係なく）を中心として左右対称であることを意味します。バランスとは、各候補値間の距離が等しく、平均化などの定量的な比較が2つ以上の候補値を含む項目間で有効であることを意味します。[9]

たとえば、典型的な 5 段階のリッカート項目の形式は次のようになります。

  1. 強く反対
  2. 同意しない
  3. 賛成でも反対でもない
  4. 同意する
  5. 強く同意する

リッカート尺度法は、ある文に対する肯定的または否定的な反応を測定する双極性尺度法です。中間の選択肢である「どちらでもない」が存在しない偶数点尺度が用いられる場合もあります。これは中立的な選択肢が排除されるため、「強制選択法」と呼ばれることもあります。 [10]中立的な選択肢は、回答者が確信を持てないときに容易に選択できる選択肢と見なされる場合があり、真の中立的選択肢であるかどうかは疑問です。1987年の研究では、5段階リッカート尺度において中間の選択肢として「未定」と「どちらでもない」を用いた場合の違いはほとんど見られませんでした。[11]

リッカート尺度は、いくつかの原因により歪む可能性があります。回答者は以下のような場合があります。

  • 極端な回答カテゴリーの使用（中心傾向バイアス）は避けるべきです。特に、極端な見解を持っていると認識されることを避けたい場合（社会的望ましさバイアスの一例）、この効果はテストの早い段階で現れることがあります。これは、被験者がより強い見解を持つ質問が続くだろうという期待によって、テストの早い段階で現れる可能性があります。つまり、早い段階での質問で、テストの後半でより強い回答を「残す」ことができるのです。この期待は、その影響がテスト全体にわたって均一ではなく、単純な一律正規化では修正できないという点で、特に有害なバイアスを生み出します。
  • 提示された発言に同意する（黙認バイアス）。例えば、発言Aとその反対意見の両方に同意するなど。この効果は、子供、発達障害のある人、高齢者、そして「喜ばせよう」という熱意を奨励し、インセンティブを与えるような制度化文化にさらされている人々において特に顕著である。
  • 誤った発言を避けたい、および/または回答が誤解されたり文脈から外れて解釈されたりした場合に回答者が不利に利用されることを恐れる可能性のある否定的な結果を回避したいという防御的な欲求から、提示された文章に同意しない。
  • 強みや弱み/機能不全の欠如（「良いふり」）を示すものとして評価されると思われる回答を提供します。
  • 弱点または障害/病状の存在を示すものとして評価されると思われる回答を提供する（「悪いふり」）。
  • 自分自身や自分の組織を、審査官や社会が自分の本当の信念よりも好ましいと考えるような見方で描写しようとする (社会的望ましさバイアス、上で説明した客観的な「善を装う」ことの主観的バージョン)。
  • 自分自身や自分の組織を、審査官や社会が自分の本当の信念よりも好ましくない/好ましくないと考えるような見方で描写しようとします（規範への反抗、上で説明した客観的な「悪を装う」ことの主観的バージョン）。

バランスのとれたキーイング（肯定的な記述と否定的な記述が同数、特に、それぞれの立場や問題に関して肯定的な記述と否定的な記述が同数）で尺度を設計すると、肯定的にキーイングされた項目への同意が否定的にキーイングされた項目への同意とバランスをとるため、同意バイアスの問題を回避できますが、防衛バイアス、中心傾向バイアス、社会的望ましさバイアスは多少問題があります。

採点と分析

質問票の記入後、各項目は個別に分析される場合もありますが、場合によっては項目の回答を合計して項目群のスコアを作成することもあります。そのため、リッカート尺度はしばしば総括尺度と呼ばれます。[要出典]

個々のリッカート尺度項目を間隔尺度データとみなせるか、それとも順序カテゴリデータとして扱うべきかについては、文献においてかなりの意見の相違があり、[12] [13]、どの方法が最も適用可能であるかについては強い確信がある。この意見の相違は、多くの点で、リッカート尺度項目が順序尺度データとして解釈される程度にまで遡ることができる。[要出典]

議論の指針となる主要な考慮事項は2つある。第一に、リッカート尺度は恣意的である。リッカート項目に割り当てられる値は、測度理論においても尺度（距離指標を決定できるもの）においても、客観的な数値的根拠を持たない。各リッカート項目に割り当てられる値は、調査を設計する研究者が、望ましい詳細レベルに基づいて決定する。しかしながら、慣例的に、リッカート項目には漸進的な正の整数値が割り当てられる傾向がある。リッカート尺度は通常2から10の範囲で、3、5、または7が最も一般的である。[14]さらに、尺度の漸進的な構造は、後続のリッカート項目が前の値よりも「より良い」回答を示すものとして扱われるようになっている。これは、リッカート尺度の逆順が必要な場合には異なる可能性がある。[要出典]

2つ目、そしておそらくより重要な点は、各項目カテゴリー間の「距離」が等距離であるかどうかです。これは伝統的に推論または仮定されています。例えば、上記の5段階リッカート尺度項目では、カテゴリー1と2の間の「距離」はカテゴリー3と4の間の「距離」と同じであると推論または仮定されています。優れた研究慣行の観点から、研究者による等距離の提示は重要です。そうでなければ、分析に偏りが生じる可能性があります。例えば、「悪い」「平均」「良い」「非常に良い」というカテゴリーを持つ4段階リッカート尺度項目では、平均以下の評価を受けるカテゴリーは1つだけであるため、すべてのカテゴリーが等距離である可能性は低いでしょう。これは、肯定的な結果に有利なバイアスをかける可能性が高いと考えられます。一方、研究者が等距離であると考えるカテゴリーを提示したとしても、回答者はそれを異なる解釈をする可能性があります。[要出典]

優れたリッカート尺度は、上記のような、明確に定義された言語的修飾語を用いて、中点を中心としたカテゴリーの対称性を提示します。このような対称的な尺度構成では、等距離にある属性は通常、より明確に観察されるか、少なくとも推測されます。リッカート尺度が対称かつ等距離にある場合、それは間隔レベルの測定のように振る舞います。つまり、リッカート尺度は確かに順序尺度ですが、適切に提示されていれば、間隔レベルの測定に近似することができます。これは有益です。なぜなら、単に順序尺度として扱われた場合、リッカート項目間の「距離」を考慮に入れなければ、貴重な情報が失われる可能性があるからです。ここで重要なのは、適切な分析の種類は、リッカート尺度がどのように提示されているかによって決まるということです。[要出典]

このような尺度の妥当性は、尺度の基礎となる区間性に依存する。2群の比較において区間性が仮定される場合、対応のある標本を用いたt検定は不適切ではない。[4]ノンパラメトリック検定を実施する場合は、標準的なウィルコクソンの符号順位検定よりも、Pratt (1959) [15]によるウィルコクソンの符号順位検定の修正が推奨される。[4]

複数のリッカート尺度質問への回答を合計することは可能ですが、その場合、すべての質問で同じリッカート尺度が用いられ、その尺度が間隔尺度の妥当な近似値である必要があります。この場合、中心極限定理により、データを潜在変数を測定する間隔データとして扱うことができます。 [要出典]合計された回答がこれらの仮定を満たす場合、分散分析などのパラメトリック統計検定を適用できます。この近似値が許容できると考えられる典型的なカットオフは、合計に含まれる項目が最低4つ、できれば8つであることです。[5] [13]

二項リッカート尺度回答を直接モデル化するには、賛成と反対の回答を別々に合計することで二項式で表すことができます。この変換後には、カイ二乗検定、コクランのQ検定、マクネマー検定などの統計手法が一般的に用いられます。カイ二乗検定、マン・ホイットニー検定、ウィルコクソンの符号順位検定、クラスカル・ワリス検定などのノンパラメトリック検定は、リッカート尺度データの分析によく用いられます。[16]

あるいは、リッカート尺度の回答は、間隔尺度を仮定することなく、回答の順序を保持した順序プロビットモデルを用いて分析することができる。順序プロビットモデルを用いることで、順序付けされた評価を間隔尺度として扱う際に生じる誤差を防ぐことができる。 [17] コンセンサスに基づく評価（CBA）は、一般的に受け入れられている客観的な基準が存在しない分野において、リッカート尺度の客観的な基準を作成するために用いることができる。コンセンサスに基づく評価（CBA）は、一般的に受け入れられている基準を改良したり、さらには検証したりするために用いることができる。[要出典]

潜在変数モデル

リッカート尺度項目の集合に対する反応を分析するための一般的な方法は、例えば因子分析や項目反応理論などを使用して、潜在変数モデルによって要約することです。[要出典]

ラッシュモデル

リッカート尺度データは、原理的には、多値ラッシュモデルを適用することで、連続体における区間推定値を得るための基礎として用いることができます。ただし、このモデルに適合するデータが得られた場合に限ります。さらに、多値ラッシュモデルは、意図したとおり、記述が態度や特性の漸進的なレベルを反映しているという仮説を検証することを可能にします。例えば、このモデルを適用すると、中立的なカテゴリーが、反対と賛成のカテゴリー間の態度や特性のレベルを表さないことがしばしば示されます。[要出典]

リッカート尺度項目のすべてのセットがラッシュ測定に使用できるわけではありません。モデルの厳密な形式公理を満たすために、データは徹底的に検証される必要があります。しかし、生のスコアはラッシュ測定の十分な統計量であり、これはゲオルク・ラッシュの意図的な選択です。したがって、生のスコアを妥当であると受け入れるのであれば、ラッシュ測定も妥当であると受け入れることができます。[要出典]

リッカート型データの視覚的表現

データ分析とプレゼンテーションにおいて重要な部分は、データの視覚化（またはプロット）です。リッカート尺度（およびその他の評価データ）のプロットについては、ロビンズとハイバーガーによる2つの論文で詳しく論じられています。[18] [19]

最初の論文では、ロビンズとハイバーガーは、いわゆる「発散積み上げ棒グラフ」の使用を推奨し、それを他の描画スタイルと比較しています。[18]

2番目の論文では、RのHHパッケージのLikert関数の使い方について説明し、その使用例を多数示しています。[19]

KooとYangによる別の論文では、5段階リッカート尺度回答のクラスター化された発散積み上げ棒グラフを作成する方法を示すPythonコードも提供されています。 [20]

測定レベル

5 つの応答カテゴリーは、測定の間隔レベルを表すとよく考えられています。しかし、これは、尺度点間の間隔が測定基準の意味における経験的観察に対応する場合にのみ当てはまります。Reips と Funke (2008) [21]は、この基準は視覚的アナログ尺度によってよりよく満たされることを示しています。実際、リッカート尺度における順序尺度レベルに疑問を投げかける現象も現れることがあります。[22]たとえば、リッカート尺度で評価された項目A、  B、  Cのセットでは、 A  >  B、B  >  C、C  >  Aのような循環関係が現れることがあります。これは、順序尺度の 推移性の公理に違反しています。

Labovitz [23]と Traylor [24]による研究では、尺度点間の知覚距離にかなり大きな歪みがあっても、リッカート尺度項目は等間隔として知覚される尺度に近いパフォーマンスを示すことが示されています。そのため、これらの項目や、質問票における等間隔とみなされる他の尺度は、多くの研究者がパラメトリック統計手法や検定に必須であると考えている等間隔の仮定に反する場合でも堅牢です。

発音

この音階を開発したレンシス・リッカートは、自分の名前を/ ˈ l ɪ k ər t / LIK -ərtと発音した。[25] [26] （つまり、LICK-ert であり、LIKE-ert ではない）。リッカートの名前は「この分野で最も間違って発音される名前の一つだ」と主張する人もいる。[27]なぜなら、多くの人がこの音階の名前を/ ˈ l aɪ k ər t / LY -kərtと発音するからである。

参照

注記

  1. ^一般に / ˈ l aɪ k ər t / LY -kərtと誤発音される

参考文献

  1. ^ Wuensch, Karl L. (2005年10月4日). 「What is a Likert Scale? and How Do You Pronounce 'Likert?'」. East Carolina University. 2024年7月21日時点のオリジナルよりアーカイブ。 2023年12月16日閲覧。
  2. ^ リッカート、レンシス(1932). 「態度測定の技法」心理学アーカイブ. 140 : 1–55 .
  3. ^ スペクター、ポール・E (1992).総括評価尺度の構成. Sage.
  4. ^ abc デリック, B; ホワイト, P (2017). 「個別リッカート質問からの2つのサンプルの比較」国際数学統計ジャーナル. 18 (3): 1– 13.
  5. ^ ab Carifio, James; Perla, Rocco (2007). 「リッカート尺度とリッカート応答形式に関する10のよくある誤解、誤解、根強い神話、都市伝説、そしてその対策」『社会科学ジャーナル』3 (3): 106–116 . doi :10.3844/jssp.2007.106.116.
  6. ^ バーンズ、アルビン、バーンズ、ロナルド (2008). 『ベーシック・マーケティング・リサーチ（第2版）』 ニュージャージー州: ピアソン・エデュケーション. pp. 245. ISBN 978-0-13-205958-9。
  7. ^ van Alphen, A.; Halfens, R.; Hasman, A.; Imbos, T. (1994). 「リッカートかラッシュか？優れた理論ほど応用できるものはない」. Journal of Advanced Nursing . 20 (1): 196– 201. doi :10.1046/j.1365-2648.1994.20010196.x. PMID  7930122.
  8. ^ Rusch, Thomas; Lowry, Paul B.; Mair, Patrick; Treiblmaier, Horst (2017). 「古典的テスト理論の限界からの脱却：項目反応理論を用いた情報システム尺度の開発と測定」（PDF） . Information & Management . 54 (2): 189– 203. doi :10.1016/j.im.2016.06.005.
  9. ^ バーンズ、アルビン、バーンズ、ロナルド (2008). 『ベーシック・マーケティング・リサーチ（第2版）』 ニュージャージー州: ピアソン・エデュケーション. pp. 250. ISBN 978-0-13-205958-9。
  10. ^ アレン、エレイン、シーマン、クリストファー (2007). 「リッカート尺度とデータ分析」.クオリティ・プログレス. pp.  64– 65.
  11. ^ アームストロング、ロバート (1987). 「5段階リッカート尺度における中間点」.知覚と運動技能. 64 (2): 359– 362. doi :10.2466/pms.1987.64.2.359. S2CID  145705789.
  12. ^ ジェイミーソン, スーザン (2004). 「リッカート尺度：その（誤用）方法」（PDF） .医学教育. 38 (12): 1217– 1218. doi :10.1111/j.1365-2929.2004.02012.x. PMID  15566531. S2CID  42509064.
  13. ^ ab Norman, Geoff (2010). 「リッカート尺度、測定レベル、そして統計の『法則』」.健康科学教育の進歩. 15 (5): 625– 632. doi :10.1007/s10459-010-9222-y. PMID  20146096. S2CID  6566608.
  14. ^ 「リッカート尺度の説明 - インタラクティブな例付き」SurveyKing . 2017年8月13日閲覧。
  15. ^ Pratt, J. (1959). 「ウィルコクソンの符号順位検定におけるゼロとタイに関する考察」アメリカ統計学会誌. 54 (287): 655– 667. doi :10.1080/01621459.1959.10501526.
  16. ^ Mogey, Nora (1999年3月25日). 「リッカート尺度を使いたいの？」学習技術普及イニシアチブヘリオット・ワット大学. 2009年3月24日時点のオリジナルよりアーカイブ。 2009年4月30日閲覧。
  17. ^ Liddell, Torrin M.; Kruschke, John K. (2018). 「計量モデルを用いた順序データの分析：何が問題になるのか？」. Journal of Experimental Social Psychology . 79 : 328–348 . doi :10.1016/j.jesp.2018.08.009. hdl : 2022/21970 .
  18. ^ Robbins, NB; Heiberger, RM (2011). 「リッカート尺度とその他の評価尺度のプロット」(PDF) . JSM Proceedings, Section on Survey Research Methods . American Statistical Association. pp.  1058– 1066.
  19. ^ ab Heiberger, RM; Robbins, NB (2014). 「リッカート尺度およびその他のアプリケーションのための発散積み上げ棒グラフのデザイン」. Journal of Statistical Software . 第57巻. アメリカ統計協会. pp.  1– 32. doi : 10.18637/jss.v057.i05 . S2CID  61139330.
  20. ^ Koo, M.; Yang, SW (2025). 「リッカート型尺度」.百科事典. 5 (1): 18. doi : 10.3390/encyclopedia5010018 .
  21. ^ Reips, Ulf-Dietrich; Funke, Frederik (2008). 「インターネットベースの調査における視覚アナログ尺度を用いた間隔レベル測定：VASジェネレーター」.行動研究方法. 40 (3): 699– 704. doi : 10.3758/BRM.40.3.699 . PMID  18697664.
  22. ^ Johanson, George A.; Gips, Crystal J. (1993年4月12日～16日). 一対比較の非推移性：有用な情報か迷惑か？(PDF) . アメリカ教育研究協会年次総会. アトランタ, ジョージア州.
  23. ^ Labovitz, S. (1967). 「測定と統計に関するいくつかの考察」. Social Forces . 46 (2): 151– 160. doi :10.2307/2574595. JSTOR  2574595.
  24. ^ トレイラー、マーク（1983年10月）「順序尺度法と間隔尺度法」市場調査協会誌25 ( 4): 297-303。
  25. ^ バビー、アール・R. (2005). 『社会調査の基礎』ベルモント、カリフォルニア州: トムソン・ワズワース、p. 174. ISBN 978-0-534-63036-2。
  26. ^ マイヤーズ、ローレンス・S.、グアリノ、アンソニー、ガムスト、グレン (2005). 『応用多変量研究：デザインと解釈』 Sage Publications. p. 20. ISBN 978-1-4129-0412-4。
  27. ^ レイサム、ゲイリー・P. (2006). 『仕事へのモチベーション：歴史、理論、研究、そして実践』 カリフォルニア州サウザンドオークス：セージ出版. p. 15. ISBN 978-0-7619-2018-2。
  • Trochim, William MK (2006年10月20日). 「リッカート尺度法」.研究手法知識ベース, 第2版. 2009年4月30日閲覧.
  • Galili, Tal (2010-04-07). 「順序カテゴリデータの相関散布図マトリックス」R統計ブログ. 2017年11月7日閲覧。
  • Uebersax, John S. Likert 尺度: 混乱を払拭する。2006 年。
  • Jebb, AT, Ng, V., & Tay, L. (2021). 主要なリッカート尺度開発の進歩に関するレビュー：1995～2019年. Frontiers in Psychology , 12, 637547. https://doi.org/10.3389/fpsyg.2021.637547
Retrieved from "https://en.wikipedia.org/w/index.php?title=Likert_scale&oldid=1322468980"