標準ステップ法

標準ステップ法（STM）は、定常状態において、徐々に流量が変化する開水路における一次元表面水位プロファイルを推定するために用いられる計算手法である。エネルギー方程式、運動量方程式、連続方程式を組み合わせ、摩擦勾配、水路勾配、水路形状、そして流量が与えられた場合に水深を求める。実際には、この手法は、米国陸軍工兵隊水文工学センター（HEC）が開発したコンピュータプログラムHEC-RASを通じて広く利用されている。^{[ 1 ]}${\displaystyle (S_{f})}$ ${\displaystyle (S_{0})}$

開水路流れの基礎

図1.エネルギー方程式の用語を定義するために使用される概念図。^{[ 2 ]}

図2.与えられた流量(Q)における流れの深さ(y)と総エネルギー(E)の関係を示す図。臨界流量、亜臨界流量、超臨界流量の位置に注目してください。

開水路流れ計算に用いられるエネルギー方程式は、ベルヌーイ方程式（ベルヌーイの原理を参照）を簡略化したもの。この方程式は、圧力水頭、標高水頭、速度水頭を考慮している。（注：流体力学では、エネルギーと水頭は同義語である。詳細は圧力水頭を参照）。開水路では大気圧の変化は無視できると仮定されるため、ベルヌーイ方程式で使用される「圧力水頭」の項は除去される。結果として得られるエネルギー方程式は以下の通りである。

${\displaystyle H=z+y+{\frac {v^{2}}{2g}}}$            式1

流量と流路形状が一定である場合、流水深と総エネルギーの間には関係があります。これは、エネルギーと流水深の関係を示すグラフ（Ey線図として広く知られています）に示されています。このグラフにおいて、エネルギーが最小となる深度は臨界深度と呼ばれます。したがって、この深度はフルード数 1に相当します。臨界深度よりも深い深度は「亜臨界」とみなされ、フルード数は1未満です。一方、臨界深度よりも浅い深度は超臨界とみなされ、フルード数は1を超えます。 ${\displaystyle (F_{n})}$

${\displaystyle F_{n}={\frac {v}{(g{\frac {A}{B}})^{0.5}}}}$            式2

定常流状態（洪水波がないなど）では、開水路の流れは、一様流、漸変流、急変流の3種類に分類できます。一様流とは、水路に沿った距離によって水深が変化しない状況を指します。これは、流れ、水路形状、粗度、水路勾配に変化がない滑らかな水路でのみ発生します。一様流の場合、水深は法線深（yn）と呼ばれます。この深さは、重力と摩擦力がつり合っている自由落下中の物体の終端速度に似ています（Moglen、2013）。^{[ 3 ]}通常、この深さはマニングの式を使用して計算されます。漸変流は、水路距離の変化あたりの水深の変化が非常に小さい場合に発生します。この場合、一様流用に開発された静水力学的関係が適用されます。この例としては、河川構造物（ダム、水門、堰など）の背後の背水、水路に狭窄部がある場合、水路勾配に小さな変化がある場合などが挙げられます。流れの急激な変化は、流下距離の変化に対する流水深の変化が大きい場合に発生します。この場合、流体静力学的な関係は解析解には適しておらず、運動量の連続性を考慮する必要があります。このような例としては、放水路のような大きな勾配変化、流れの急激な狭窄／拡大、跳水などが挙げられます。

水面プロファイル（徐々に変化する流れ）

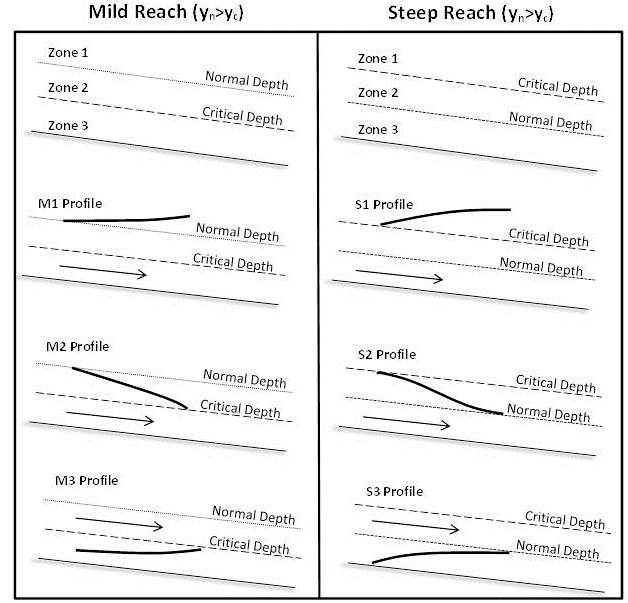
STMは通常、緩やかに変化する流れを経験する水路の「表層水プロファイル」、つまり水路深の縦断的表現を作成するために使用されます。これらの遷移は、流路条件（緩やかまたは急）と、発生する遷移の種類に基づいて分類できます。緩やかな流路は、通常水深が亜臨界（yn > yc）の場合に発生し、急な流路は、通常水深が超臨界（yn < yc）の場合に発生します。遷移はゾーンによって分類されます（図3参照）。

図3. この図は、徐々に変化する流量条件下での急勾配区間と緩勾配区間における異なるクラスの地表水プロファイルを示しています。^{[ 4 ]}注: 急勾配区間の列には「急勾配区間(yn<yc)」とラベルを付ける必要があります。

上記の地表水プロファイルは、徐々に変化する流れの支配方程式に基づいています（下記参照）。

${\displaystyle {\frac {dy}{dx}}={\frac {S_{0}-S_{f}}{1-F_{n}^{2}}}}$            式3

この方程式 (および関連する地表水プロファイル) は、次の仮定に基づいています。

• 傾斜は比較的小さい
• 関心のある観測所における水路断面が既知である
• 静水圧分布がある

標準ステップ法による計算

STMは反復プロセスを通じて式3を数値的に解きます。これは二分法またはニュートン・ラプソン法を用いて行うことができ、基本的には式4と式5を用いて、指定された場所における水深を変化させ、その場所における全水頭を求めます。^{[ 5 ]}

${\displaystyle H_{2}=H_{1}-h_{f}}$            式4

${\displaystyle H_{2}=h_{vel}+h_{ele}}$            式5

この手法を使用するには、モデル化するシステムについてある程度の理解が不可欠です。段階的に変化する流れの遷移ごとに、両方の境界条件を把握し、その遷移の長さを計算する必要があります。（例えば、M1プロファイルの場合、下流境界条件における上昇、上流境界条件における法線深度、そして遷移の長さを求める必要があります。）段階的に変化する流れの遷移の長さを求めるには、境界条件の高さにおいて、高さではなく「ステップ長」を方程式4と方程式5が一致するまで繰り返し計算します。（例えば、M1プロファイルの場合、位置1は下流条件であり、高さが法線深度と等しい位置2を求めます。）

ニュートン・ラプソン数値法

Excel などのコンピュータ プログラムには、手動による反復処理の代わりに実際の深度を自動的に計算できる反復処理またはゴール シーク機能が含まれています。

概念的な地表水プロファイル（水門）

図 4.緩やかな区間 (上) と急な区間 (下) における水門に関連する地表水プロファイルの図解。

図 4 は、緩やかな区間 (上) と急な区間 (下) にある水門に関連した異なる地表水プロファイルを示しています。水門によってシステムが絞られ、水門のすぐ上流で「逆流」プロファイルが生じることに注意してください。緩やかな区間では水門の下流で跳水が発生しますが、急な区間では水門の上流で跳水が発生します。段階的に変化する流れの方程式と関連する数値手法 (標準ステップ法を含む) では跳水の動きを正確にモデル化できないことに注意することが重要です。^{[ 6 ]}詳細については、 「長方形チャネルの跳水」のページを 参照してください。以下では、概念モデルを使用して STM による地表水プロファイルを作成する問題の例を示します。

例題

解決

図3と、ゲート上流および下流の状況、そしてゲート両側の水深値を用いることで、ゲート上流および下流のプロファイルの大まかな推定値を生成することができます。上流では、水面は通常の水深0.97mからゲート地点で9.21mまで上昇する必要があります。緩やかな勾配でこれを実現する唯一の方法は、M1プロファイルに従うことです。下流でも同じ論理が適用され、ゲートから水面はM3プロファイルに従い、通常水深の共役水深に達するまで上昇し、その時点で跳水が発生し、水面は通常水深まで上昇します。

ステップ4： ニュートン・ラプソン法を用いて、M1およびM3の表層水プロファイルを解析します。上流部と下流部は別々にモデル化し、上流部の初期水深を9.21m、下流部の初期水深を0.15mとします。下流水深は、法線水深の共役水深に達するまでモデル化する必要があります。共役水深に達すると、跳水が発生します。提示されたソリューションでは、スプレッドシートで問題を解く方法を説明し、計算結果を列ごとに示しています。Excelでは、ゴールシーク機能を使用して、手動で反復する代わりに、列2の水深推定値を変更することで、列15を0に設定できます。

表1：ニュートン・ラプソン法による下流水面標高計算のスプレッドシート

ステップ 5:さまざまなプロファイルの結果を結合して表示します。

ゲート上流約2,200メートルで正常深度に達しました。

ステップ6: HEC-RASモデリング環境で問題を解決します。

HEC-RAS の操作の複雑さについては、この Wikipedia ページで詳しく説明することはできません。さらに詳しく知りたい方は、HEC-RAS ユーザーズマニュアルが優れた学習ツールです。プログラムは無料で公開されています。

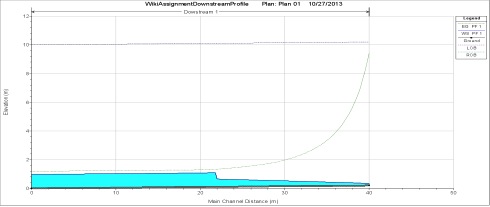
下の最初の2つの図は、HEC-RASによってモデル化された上流および下流の水面プロファイルです。また、2つの異なる手法で異なる観測点において推定されたプロファイルの差異を比較した表も提供されており、2つの手法間の一貫性を示しています。2つの異なる手法は類似した水面形状をモデル化しましたが、標準ステップ法では、ゲートの上流および下流で水流が通常深度に到達するまでの距離が長くなると予測されました。この水面の伸びは、計算中に2つの観測点間の平均勾配を仮定したことに伴う誤差によって発生します。dx値を小さくすると、この誤差が減少し、より正確な水面プロファイルが得られます。

HEC-RASモデルは、水門上流側で水位が9.21メートルまで逆流すると計算しました。これは手動で計算した値と同じです。水門上流約1,700メートルで正常な水深に達しました。

HEC-RAS は、水門の下流 18 メートルで水跳が発生するとモデル化しました。

参考文献

1. USACE. 「HEC-RAS バージョン4.1 ユーザーズマニュアル」. 水文工学センター、カリフォルニア州デイビス。{{cite web}}:欠落または空|url=(ヘルプ)
2. Chaudhry, MH (2008).開水路流れ. ニューヨーク: Springer.
3. Moglen, G. 「Lecture Notes from CEE 4324/5894: Open Channel Flow, Virginia Tech」 2012年11月5日時点のオリジナルよりアーカイブ。 2013年4月24日閲覧。
4. Chow, VT (1959).開水路水理学. ニューヨーク: マグロウヒル.
5. Chaudhry, MH (2008).開水路流れ. ニューヨーク: Springer.
6. Chaudhry, MH (2008).開水路流れ. ニューヨーク: Springer.