オイラー線

  オイラーの直線、9点円の中心

  中線（重心で交差）

  高度（垂心で交差）

  辺の中点から垂線（外心で交差）

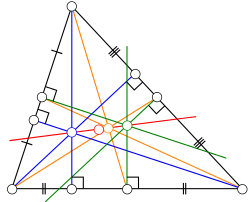
幾何学において、オイラー線（オイラーせん、英: Euler line ）は、レオンハルト・オイラー（/ ˈ ɔɪ l ər / OY -lər）にちなんで名付けられた、正三角形ではない任意の三角形から決定される直線である。これは三角形の中心線であり、垂心、外心、重心、エクセター点、そして三角形の九点円の中心など、三角形から決定されるいくつかの重要な点を通過する。^{[ 1 ]}

三角形のオイラー線の概念は、四辺形や四面体などの他の図形のオイラー線にも拡張されます。

三角形の中心はオイラー直線上にある

個々のセンター

オイラーは1765年に、任意の三角形において垂心、外心、重心が一直線上にあることを示した。^{[ 2 ]}この性質は、オイラーの時代には定義されていなかったものの、別の三角形の中心である九点心にも当てはまる。正三角形ではこれらの4点は一致するが、それ以外の三角形ではこれらはすべて互いに異なるため、オイラー直線はこれらのうちの任意の2点によって決定される。

オイラー直線上にある他の注目すべき点には、ロンシャン点、シフラー点、エクセター点、ゴッサール・パースペクターなどがあります。^{[ 1 ]}しかし、内心は一般にオイラー直線上にありません。^{[ 3 ]}内心は二等辺三角形の場合にのみオイラー直線上にあり、^{[ 4 ]}二等辺三角形の場合、オイラー直線は三角形の対称軸と一致し、すべての三角形の中心を含みます。

基準三角形の接線三角形は、基準三角形の頂点において、基準三角形の外接円に接する。接線三角形の外心は、基準三角形のオイラー線上にある。^{[ 5 ] : p. 447 [ 6 ] : p.104, #211, p.242, #346} 直交三角形と接線三角形の相似中心もオイラー線上にある。^{[ 5 ] : p. 447 [ 6 ] : p. 102}

証明

ベクトル証明

三角形をとする。外心、重心、垂心が一直線上にあることの証明は、自由ベクトルに依存する。まず前提条件を述べる。まず、 は関係式を満たす 。${\displaystyle ABC}$ ${\displaystyle O}$ ${\displaystyle G}$ ${\displaystyle H}$ ${\displaystyle G}$

${\displaystyle {\vec {GA}}+{\vec {GB}}+{\vec {GC}}=0.}$

これは、の絶対重心座標がであるという事実から導かれる。さらに、シルベスターの問題^{[ 7 ]}は次のように表される。 ${\displaystyle G}$ ${\displaystyle {\frac {1}{3}}:{\frac {1}{3}}:{\frac {1}{3}}}$

${\displaystyle {\vec {OH}}={\vec {OA}}+{\vec {OB}}+{\vec {OC}}。}$

さて、ベクトルの加算を使って、次のように推論します。

${\displaystyle {\vec {GO}}={\vec {GA}}+{\vec {AO}}\,{\mbox{(三角形内 }}AGO{\mbox{)}},\,{\vec {GO}}={\vec {GB}}+{\vec {BO}}\,{\mbox{(三角形内 }}BGO{\mbox{)}},\,{\vec {GO}}={\vec {GC}}+{\vec {CO}}\,{\mbox{(三角形内 }}CGO{\mbox{)}}。}$

これら3つの関係を項ごとに加算すると、次の式が得られます。

${\displaystyle 3\cdot {\vec {GO}}=\left(\sum \limits _{\scriptstyle {\rm {cyc}}}{\vec {GA}}\right)+\left(\sum \limits _{\scriptstyle {\rm {cyc}}}{\vec {AO}}\right)=0-\left(\sum \limits _{\scriptstyle {\rm {cyc}}}{\vec {OA}}\right)=-{\vec {OH}}.}$

結論として、、であり、3 つの点、、および(この順序で) は同一直線上にあります。 ${\displaystyle 3\cdot {\vec {OG}}={\vec {OH}}}$ ${\displaystyle O}$ ${\displaystyle G}$ ${\displaystyle H}$

ドリエの著書^{[ 7 ]}では、オイラー直線とシルベスターの問題は一つの証明にまとめられている。しかし、シルベスターの問題の証明のほとんどは、オイラー直線とは独立して、自由ベクトルの基本的な性質に依存している。

プロパティ

中心間の距離

オイラー直線上では、重心Gは外心Oと垂心Hの間にあり、垂心からは外心より2倍離れている。^{[ 6 ]：p.102}

${\displaystyle GH=2GO;}$

${\displaystyle OH=3GO.}$

線分GHは直交重心円の直径です。

9点円の中心Nは、垂心と外心の中間にあるオイラー線に沿って位置する。 ^{[ 1 ]}

${\displaystyle ON=NH,\quad OG=2\cdot GN,\quad NH=3GN.}$

したがって、オイラー直線は、外心O が位置 0、重心Gが2 t、9 点中心が 3 t、垂心H が6 tにある数直線上に、あるスケール係数tで再配置できます。

さらに、オイラー線に沿った重心と外心の間の距離の二乗は、外接半径R ^{2の二乗よりも、辺の長さ}a、b、cの二乗の和の9分の1に等しい量だけ小さい：^{[ 6 ]：p.71}

${\displaystyle GO^{2}=R^{2}-{\tfrac {1}{9}}(a^{2}+b^{2}+c^{2}).}$

さらに、^{[ 6 ] : p.102}

${\displaystyle OH^{2}=9R^{2}-(a^{2}+b^{2}+c^{2});}$

${\displaystyle GH^{2}=4R^{2}-{\tfrac {4}{9}}(a^{2}+b^{2}+c^{2}).}$

表現

方程式

A、B、Cを基準三角形の頂点角とし、 x  : y  : zを三線座標上の変数点とすると、オイラー直線の方程式は次のようになる。

${\displaystyle \sin(2A)\sin(BC)x+\sin(2B)\sin(CA)y+\sin(2C)\sin(AB)z=0.}$

重心座標 におけるオイラー直線の方程式は^{[ 8 ]}である。${\displaystyle \alpha :\beta :\gamma }$

${\displaystyle (\tan C-\tan B)\alpha +(\tan A-\tan C)\beta +(\tan B-\tan A)\gamma =0.}$

パラメトリック表現

オイラー直線を表す別の方法は、パラメータtで表すことである。外心（三線座標系）と垂心（三線座標系）から始めて、垂心を除くオイラー直線上のすべての点は三線座標系で与えられる。 ${\displaystyle \cos A:\cos B:\cos C}$ ${\displaystyle \sec A:\sec B:\sec C=\cos B\cos C:\cos C\cos A:\cos A\cos B),}$

${\displaystyle \cos A+t\cos B\cos C:\cos B+t\cos C\cos A:\cos C+t\cos A\cos B}$

あるtに対して、これら 2 点の三線分の線形結合として形成されます。

例えば：

• 外心にはパラメータ値に対応する三線がある${\displaystyle \cos A:\cos B:\cos C,}$ ${\displaystyle t=0.}$
• 重心はパラメータ値に対応する三線を持つ${\displaystyle \cos A+\cos B\cos C:\cos B+\cos C\cos A:\cos C+\cos A\cos B,}$ ${\displaystyle t=1.}$
• 9点の中心にはパラメータ値に対応する三線がある${\displaystyle \cos A+2\cos B\cos C:\cos B+2\cos C\cos A:\cos C+2\cos A\cos B,}$ ${\displaystyle t=2.}$
• ロンシャン点にはパラメータ値に対応する三線がある${\displaystyle \cos A-\cos B\cos C:\cos B-\cos C\cos A:\cos C-\cos A\cos B,}$ ${\displaystyle t=-1.}$

スロープ

直交座標系において、三角形の辺の傾きを、オイラー直線の傾きを と表すと、これらの傾きは^{[ 9 ]}に従って関係付けられる^：補題1 ${\displaystyle m_{1},}$ ${\displaystyle m_{2},}$ ${\displaystyle m_{3},}$ ${\displaystyle m_{E}}$

${\displaystyle m_{1}m_{2}+m_{1}m_{3}+m_{1}m_{E}+m_{2}m_{3}+m_{2}m_{E}+m_{3}m_{E}}$

${\displaystyle +3m_{1}m_{2}m_{3}m_{E}+3=0.}$

したがって、オイラー直線の傾き（有限であれば）は、辺の傾きを使って次のように表すことができます。

${\displaystyle m_{E}=-{\frac {m_{1}m_{2}+m_{1}m_{3}+m_{2}m_{3}+3}{m_{1}+m_{2}+m_{3}+3m_{1}m_{2}m_{3}}}.}$

さらに、オイラー直線が鋭角三角形の辺BCに平行となるのは、 ^{[ 9 ]：p.173} の場合のみである。${\displaystyle \tan B\tan C=3.}$

内接正三角形との関係

与えられた三角形に内接する正三角形の重心の軌跡は、与えられた三角形のオイラー線に垂直な2本の線によって形成される。^{[ 10 ]：コロ4}

特別な三角形

直角三角形

直角三角形において、オイラー直線は斜辺の中線と一致します。つまり、オイラー直線は直角頂点とその反対側の辺の中点の両方を通ります。これは、直角三角形の垂心（高低の交点）が直角頂点にあたり、外心（辺の垂直二等分線の交点）が斜辺の中点にあたるためです。

二等辺三角形

二等辺三角形のオイラー線は対称軸と一致します。二等辺三角形の内心はオイラー線上にあります。

正中三角形

自己中線三角形（中線が辺と同じ比率で逆の順序になっている三角形）のオイラー線は、中線の1つに垂直です。 ^{[ 11 ]}

平行オイラー直線を持つ三角形の系

フェルマー・トリチェリ点F ₁とF ₂を持つ三角形ABCを考える。A 、B、C、F ₁、F ₂から選ばれた頂点を持つ10個の三角形のオイラー直線は、三角形ABCの​​重心で一致する。^{[ 12 ]}

垂心系（それぞれの点が三角形の垂心となり、他の3点を頂点とする4つの点の集合）によって形成される4つの三角形のオイラー線は、すべての三角形に共通する9点の中心で一致する。^{[ 6 ]：p.111}

一般化

四辺形

凸四辺形において、準直交心H、面積の重心G、準外心Oはオイラー直線上でこの順序で一直線上にあり、 HG = 2 GOである。^{[ 13 ]}

四面体

四面体は、4つの三角形の面で囲まれた三次元の物体です。四面体を構成する7本の直線は、その重心で交わり、6つの中面はモンジュ点で交差します。また、すべての頂点を通る外接球面があり、その中心は外心です。これらの点は、三角形の「オイラー線」と同様に、四面体の「オイラー線」を定義します。重心は、この線に沿ったモンジュ点と外心の中心点です。12点球の中心もオイラー線上にあります。

単体多面体

単体多面体とは、その面がすべて単体（単体の複数形）である多面体である。例えば、すべての多角形は単体多面体である。このような多面体に関連付けられたオイラー直線は、その重心と質量の外心によって定まる直線である。このオイラー直線の定義は、上記の定義を一般化したものである。^{[ 14 ]}

が多角形であると仮定します。オイラー直線は、以下のように の対称性に影響を受けます。${\displaystyle P}$ ${\displaystyle E}$ ${\displaystyle P}$

1. が鏡映対称線 を持つ場合、 はまたは 上の点のいずれかになります。${\displaystyle P}$ ${\displaystyle L}$ ${\displaystyle E}$ ${\displaystyle L}$ ${\displaystyle L}$
2. に回転対称中心がある場合、 となります。${\displaystyle P}$ ${\displaystyle C}$ ${\displaystyle E=C}$

関連する構成

三角形のキーパート放物線は、三角形の2辺（2辺を延長）に接し、オイラー線を準線とする唯一の放物線である。^{[ 15 ]：63ページ}

参考文献

1. キンバリング、クラーク (1998). 「三角形の中心と中心三角形」. Congressus Numerantium . 129 : i– xxv, 1– 295.
2. オイラー、レオンハルト(1767)。「Solutio facilis questionatum quorundam geomeorum difficillimorum」 [いくつかの難しい幾何学的問題の簡単な解決策]。Novi Commentarii Academiae Scientarum Imperialis Petropolitanae。11 : 103–123.E325。オペラオムニア、シリーズに転載。 I、vol. XXVI、139 ～ 157 ページ、Societas Scientiarum Naturalium Helveticae、ローザンヌ、1953 年、MR 0061061。概要: ダートマス大学。 
3. シャットシュナイダー、ドリス、キング、ジェームズ (1997). 『幾何学の活用：学習、教育、研究におけるダイナミックソフトウェア』アメリカ数学会. pp.  3– 4. ISBN 978-0883850992。
4. Edmonds, Allan L.; Hajja, Mowaffaq; Martini, Horst (2008)、「直交中心の単体と双正則性」、Results in Mathematics、52 ( 1– 2): 41– 50、doi : 10.1007/s00025-008-0294-4、MR 2430410、S2CID 121434528、ユークリッド三角形の内心が、その重心と外心を結ぶオイラー線上にあるのは、三角形が二等辺三角形である場合のみであることはよく知られています。  。
5. レバーシャ、ジェリー; スミス、GC (2007年11月)、「オイラーと三角形の幾何学」、数学ガゼット、91 (522): 436– 452、doi : 10.1017/S0025557200182087、JSTOR 40378417、S2CID 125341434  。
6. Altshiller-Court, Nathan, College Geometry , Dover Publications, 2007 (orig. Barnes & Noble 1952).
7. ドリエ、ハインリッヒ「初等数学100大問題。その歴史と解答」ドーバー出版、ニューヨーク、1965年、ISBN 0-486-61348-8、141ページ（オイラーの直線）と142ページ（シルベスターの問題）
8. Scott, JA、「三角形幾何学における面積座標の使用例」、 Mathematical Gazette 83、1999年11月、472-477。
9. Wladimir G. Boskoff、Laurent¸iu Homentcovschi、Bogdan D. Suceava、「GossardのPerspectorと射影的帰結」、Forum Geometricorum、第13巻（2013年）、169-184。[1]
10. Francisco Javier Garc ́ıa Capita ́n、「相似内接三角形の重心の軌跡」、 Forum Geometricorum 16、2016年、257–267。http ://forumgeom.fau.edu/FG2016volume16/FG201631.pdf
11. Parry, CF (1991)、「シュタイナー・レームスと自動中位三角形」、The Mathematical Gazette、75 (472): 151– 154、doi : 10.2307/3620241、JSTOR 3620241 。
12. ベルホフ、ニコライ・イワノフ. 「10本の並行オイラー線」, Forum Geometricorum 9, 2009, pp. 271–274. http://forumgeom.fau.edu/FG2009volume9/FG200924index.html
13. ミャキシェフ、アレクセイ（2006）「四辺形に関連する2つの注目すべき線について」（PDF）、フォーラム幾何学、6：289–295。
14. Tabachnikov, Serge; Tsukerman, Emmanuel (2014年5月)、「質量の外心と一般化オイラー線」、離散幾何学と計算幾何学、51 (4): 815– 836、arXiv : 1301.0496、doi : 10.1007/s00454-014-9597-2、S2CID 12307207 。
15. Scimemi, Benedetto、「三角形のシュタイナー楕円に関する単純な関係」、Forum Geometricorum 10、2010年：55–77。

外部リンク

• オイラー線上にある複数の三角形の中心を表示するインタラクティブ アプレット。
• Wolframデモンストレーションプロジェクトにおける「オイラー直線」と「非ユークリッド三角形連続体」
• ダイナミックジオメトリスケッチにおける9点円錐曲線とオイラー直線の一般化、オイラー直線のさらなる一般化、四辺形と六角形の準オイラー直線
• ボゴモルニー、アレクサンダー、「高度とオイラー線」および「オイラー線と9点円」、Cut-the-Knot
• キンバリング、クラーク、「オイラー直線上の三角形の中心」、三角形の中心
• GhostarchiveとWayback Machineにアーカイブ：Stankova, Zvezdelina（2016年2月1日）、「Triangles have a Magic Highway」、Numberphile、YouTube
• ワイスタイン、エリック W. 「オイラー線」。マスワールド。