有限要素法
有限要素解析を用いた非対称衝突時の自動車の変形の可視化

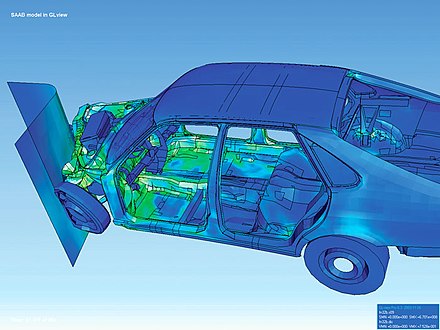
有限要素法（FEM ）は、工学および数学モデリングにおいて生じる微分方程式を数値的に解くための一般的な手法です。対象となる典型的な問題領域には、構造解析、熱伝達、流体流動、物質輸送、電磁ポテンシャルといった伝統的な分野が含まれます。必要な計算は通常、コンピュータを用いて実行されます。高速スーパーコンピュータを用いることで、より優れた解を得ることができ、大規模かつ最も複雑な問題を解く際にしばしば必要となります。

FEM は、2 または 3 空間変数の偏微分方程式(つまり、一部の境界値問題)を解く一般的な数値手法です。また、高次元の問題を FEM で解く研究もあります。[ 1 ]問題を解くために、FEM は大規模なシステムを有限要素と呼ばれるより小さく単純な部分に分割します。これは、空間次元における特定の空間離散化によって実現され、オブジェクトのメッシュ(有限個の点を持つ解の数値領域) の構築によって実装されます。境界値問題の FEM 定式化は、最終的に代数方程式のシステムをもたらします。この方法は、領域上の未知の関数を近似します。[ 2 ]これらの有限要素をモデル化する単純な方程式は、問題全体をモデル化する、より大きな方程式のシステムに組み立てられます。FEM は、変分法を介して関連する誤差関数を最小化することにより、解を近似します。

FEM を使用して現象を研究または分析することを、有限要素解析(FEA) と呼ぶこともあります。

基本概念

2Dメッシュの例
FEMソフトウェアを用いて磁気問題の解を求める前に解析者が作成したFEMメッシュ。色は解析者が各ゾーンに材料特性を設定していることを示しています。この例では、導線コイルはオレンジ色、強磁性体（おそらく鉄）は水色、空気は灰色で示されています。形状はシンプルに見えますが、FEMソフトウェアを用いずに方程式のみでこの設定の磁場を計算するのは非常に困難です。
FEM_2Dソリューションの例
左側の問題に対する有限要素法（FEM）による解は、円筒形の磁気シールドを用いています。強磁性の円筒部分は、コイルによって生成された磁場を逸らすことで、円筒内部の領域（右側の長方形領域）をシールドします。色は磁束密度の振幅を表し、挿入図の凡例のスケールで示されています。赤色は高振幅です。円筒内部の領域は低振幅（濃い青色で、磁束線の間隔が広い）であり、シールドが設計通りに機能していることを示しています。

ドメイン全体をより単純な部分に分割することにはいくつかの利点がある。[ 3 ]

  • 複雑な形状の正確な表現。
  • 異なる材料特性の包含;
  • 全体的なソリューションの簡単な表現。そして
  • ローカル効果のキャプチャ。

この方法を使用する一般的なアプローチには、次の手順が含まれます。

  1. 問題の領域をサブドメインの集合に分割し、各サブドメインを元の問題の要素方程式のセットで表します。
  2. すべての要素方程式セットを体系的に再結合して、最終的な計算のためのグローバル方程式システムを作成します。

全体方程式系では既知の解法技術が使用され、元の問題の初期値から計算して数値的な答えを得ることができます。

上記の最初のステップでは、要素方程式は、調査対象となる元の複素方程式を局所的に近似する単純な方程式です。元の方程式は、多くの場合、偏微分方程式(PDE) です。このプロセスの近似を説明するために、FEM は一般にガラーキン法の特殊なケースとして導入されます。数学的な言葉で言えば、このプロセスは、残差と重み関数の内積の積分を作成し、その積分を 0 に設定することです。簡単に言えば、試行関数を PDE に当てはめることによって近似誤差を最小化する手順です。残差は試行関数によって生じる誤差であり、重み関数は残差を投影する多項式近似関数です。このプロセスでは、PDE からすべての空間導関数を除去し、次を使用して PDE を局所的に近似します。

これらの方程式群は要素方程式です。基礎となる偏微分方程式が線形であれば、これらの方程式群も線形であり、逆もまた同様です。定常問題で生じる代数方程式群は、数値線形代数法を用いて解きます。一方、過渡問題で生じる常微分方程式群は、オイラー法やルンゲ・クッタ法などの標準的な手法を用いた数値積分によって解きます。

上記の2番目のステップでは、サブドメインのローカルノードからドメインのグローバルノードへの座標変換により、要素方程式からグローバル方程式系が生成されます。この空間変換には、参照座標系に対する適切な方向調整が含まれます。このプロセスは、サブドメインから生成された座標データ を用いて、FEMソフトウェアを用いて実行されることがよくあります。

FEM の実際の応用は有限要素解析 (FEA) として知られています。工学で応用される FEA は、工学解析を実行するための計算ツールです。複雑な問題をより小さな要素に分割するためのメッシュ生成技術の使用や、FEM アルゴリズムでコード化されたソフトウェアの使用が含まれます。FEA を適用する場合、複雑な問題は通常、オイラー・ベルヌーイの梁方程式、熱方程式、ナビエ・ストークス方程式などの基礎となる物理学を持つ物理システムであり、偏微分方程式または積分方程式のいずれかで表現されます。一方、複雑な問題の分割されたより小さな要素は、物理システム内の異なる領域を表します。

FEA は、複雑なドメイン (車や石油パイプラインなど) における問題の解析に使用できます。ドメインが変化する (例: 移動する境界を持つ固体反応中)、必要な精度がドメイン全体で変化する、またはソリューションが滑らかでない場合に使用されます。 FEA シミュレーションは、さまざまな高忠実度状況に対して複雑なプロトタイプを何度も作成してテストする手間を省くため、貴重なリソースとなります。[ 4 ]たとえば、正面衝突シミュレーションでは、車の前部などの重要な領域の予測精度を高め、車の後部では精度を下げて、シミュレーションのコストを削減することができます。 もう 1 つの例は数値天気予報で、比較的穏やかな領域よりも、大気中の熱帯低気圧や海洋の渦など、高度に非線形な現象の発達を正確に予測することがより重要です。

このアプローチの明確で詳細かつ実践的な説明は、教科書『エンジニアのための有限要素法』に掲載されています。[ 5 ]

歴史

FEM の発明日を特定することは困難ですが、この手法は土木工学や航空工学における複雑な弾性および構造解析問題を解く必要性から生まれました。[ 6 ]その発展は、1940 年代初頭のAlexander Hrennikoff [ 7 ]とRichard Courant [ 8 ]の研究に遡ります。もう一人の先駆者はIoannis Argyrisです。ソ連では、FEM の実用化の導入は通常Leonard Oganesyanと結び付けられます。[ 9 ] FEM は、 1950 年代後半から 1960 年代初頭にかけて、中国でFeng Kangによってダム建設の計算に基づき独立に再発見され、変分原理に基づく「有限差分法」と呼ばれました。これらの先駆者たちが使用したアプローチは異なりますが、連続領域を一連の離散的なサブドメイン (通常は要素) に メッシュ分割するという重要な特徴を共有しています。

レンニコフの研究は格子アナロジーを用いて領域を離散化するのに対し、クーラントのアプローチは、円筒のねじれ問題から生じる2階楕円偏微分方程式を解くために、領域を有限の三角形のサブ領域に分割する。クーラントの貢献は進化的なものであり、レイリー卿、ヴァルター・リッツ、ボリス・ガラーキンによって開発された偏微分方程式に関する膨大な先行研究成果を援用した。

FEM の応用は、シュトゥットガルト大学のJH Argyrisと彼の同僚、カリフォルニア大学バークレー校のRW Cloughと彼の同僚、スウォンジー大学のOC Zienkiewiczと彼の同僚Ernest Hinton、Bruce Irons [ 10 ] ら、パリ第 6 大学の Philippe G. Ciarlet、コーネル大学の Richard Gallagher と彼の同僚たちの開発により、1960 年代から 1970 年代にかけて勢いを増しました。この期間中、利用可能なオープンソースのFEMプログラムによってさらなる推進力がもたらされました。NASAはNASTRANのオリジナル バージョンを後援しました。カリフォルニア大学バークレー校は有限要素プログラム SAP IV [ 11 ]を、後にOpenSees を広く利用できるようにしました。ノルウェーでは、船級協会Det Norske Veritas（現DNV GL）が1969年に船舶解析用にSesamを開発しました。 [ 12 ] FEMの厳密な数学的基礎は、1973年にギルバート・ストラングとジョージ・フィックスによる出版物によって提供されました。[ 13 ]この手法はその後、電磁気学、伝熱、流体力学など、さまざまな工学分野の物理システムの数値モデリングに一般化されました。[ 14 ] [ 15 ]

技術的な議論

有限要素法の構造

有限要素法は、変分定式化、離散化戦略、1 つ以上の解析アルゴリズム、および後処理手順によって特徴付けられます。

変分法の例としては、ガラーキン法、不連続ガラーキン法、混合法など があります。

離散化戦略とは、(a)有限要素メッシュの作成、(b)参照要素上の基底関数（形状関数とも呼ばれる）の定義、(c)参照要素のメッシュ要素へのマッピングを含む、明確に定義された一連の手順を指します。離散化戦略の例としては、hバージョン、pバージョン、hpバージョン、x-FEM、アイソジオメトリック解析などがあります。それぞれの離散化戦略には、それぞれ長所と短所があります。離散化戦略を選択する際の合理的な基準は、特定のモデルクラスにおいて、最も広範な数学モデルセットに対してほぼ最適なパフォーマンスを実現することです。

様々な数値解法アルゴリズムは、直接法と反復法という2つの大きなカテゴリに分類できます。これらのアルゴリズムは、変分定式化と離散化戦略の選択に応じて変化する行列のスパース性を利用するように設計されています。

ポスト処理手順は、有限要素解から関心のあるデータを抽出するように設計されています。解の検証要件を満たすために、ポストプロセッサは関心のある量に関して事後誤差推定を行う必要があります。近似誤差が許容範囲を超える場合、自動適応プロセスまたは解析者による操作によって離散化を変更する必要があります。非常に効率的なポストプロセッサの中には、超収束の実現を可能にするものもあります。

例示問題P1とP2

次の 2 つの問題は有限要素法を示しています。

P1 はが与えられ、は の未知の関数、は に関するの2次導関数である1次元の問題です 。  P1 :{あなた″（×）＝f（×） で （0、1）、あなた（0）＝あなた（1）＝0、{\displaystyle {\text{P1}}:{\begin{cases}u''(x)=f(x){\text{in}}(0,1),\\u(0)=u(1)=0,\end{cases}}}f{\displaystyle f}あなた{\displaystyle u}×{\displaystyle x}あなた″{\displaystyle u''}あなた{\displaystyle u}×{\displaystyle x}

P2は2次元問題（ディリクレ問題） であるP2 :{あなた××（×、y）+あなたyy（×、y）＝f（×、y） で Ω、あなた＝0 の上 ∂Ω、{\displaystyle {\text{P2}}:{\begin{cases}u_{xx}(x,y)+u_{yy}(x,y)=f(x,y)&{\text{ in }}\Omega ,\\u=0&{\text{ on }}\partial }}\Omega ,\end{cases}}}

ここで、 は境界が滑らかな平面上の連結された開領域（例えば、滑らかな多様体や多角形）であり、および はそれぞれおよび に関する2次導関数を表します。 Ω{\displaystyle \オメガ}（×、y）{\displaystyle (x,y)}∂Ω{\displaystyle \partial \Omega }あなた××{\displaystyle u_{xx}}あなたyy{\displaystyle u_{yy}}×{\displaystyle x}y{\displaystyle y}

問題P1は、原始微分を計算することで直接解くことができます。しかし、境界値問題（BVP）を解くこの方法は、空間次元が1次元の場合のみ有効です。高次元の問題や のような問題には一般化できません。そのため、ここではP1に対する有限要素法を展開し、そのP2への一般化について概説します。 あなた+V″＝f{\displaystyle u+V''=f}

説明は 2 つのステップで進みます。これは、FEM を使用して境界値問題 (BVP) を解くために必要な 2 つの重要なステップを反映しています。

  • 最初のステップでは、元のBVPを弱形式で言い換えます。このステップでは通常、計算はほとんど、あるいは全く必要ありません。変換は紙上で手作業で行われます。
  • 2 番目のステップは離散化です。ここでは、弱形式が有限次元空間で離散化されます。

この第2ステップの後、大規模だが有限次元の線形問題に対する具体的な公式が得られ、その解は元のBVPを近似的に解く。この有限次元問題は、コンピュータ上で実装される。

弱い定式化

最初のステップは、P1 と P2 を同等の弱い定式化に変換することです。

P1の弱形

がP1を解くとき、変位境界条件を満たす任意の滑らかな関数、すなわち、およびにおいて、次式が成り立ちます。 あなた{\displaystyle u}v{\displaystyle v}v＝0{\displaystyle v=0}×＝0{\displaystyle x=0}×＝1{\displaystyle x=1}

逆に、任意の滑らかな関数に対して(1)式を満たす場合、これがP1を解くことを示すことができる。証明は2回連続微分可能（平均値定理）な場合の方が容易であるが、分布関数的な意味でも 証明できる。あなた{\displaystyle u}あなた（0）＝あなた（1）＝0{\displaystyle u(0)=u(1)=0}v（×）{\displaystyle v(x)}あなた{\displaystyle u}あなた{\displaystyle u}

(1)の右辺の 部分積分を用いて新しい演算子またはマップを定義する。ϕ（あなた、v）{\displaystyle \phi (u,v)}

ここで、 という仮定を使用しています。 v（0）＝v（1）＝0{\displaystyle v(0)=v(1)=0}

P2の弱形

グリーン恒等式の形式を使って部分積分すると、P2を解くと、任意の に対して次のように定義できることがわかります。あなた{\displaystyle u}ϕ（あなた、v）{\displaystyle \phi (u,v)}v{\displaystyle v}∫Ωfvds＝−∫Ω∇あなた⋅∇vds≡−ϕ（あなた、v）、{\displaystyle \int _{\Omega }fv\,ds=-\int _{\Omega }\nabla u\cdot \nabla v\,ds\equiv -\phi (u,v),}

ここで、は勾配を表し、は2次元平面におけるドット積を表す。さらに、は、 上で零となるの1回微分可能な関数の適切な空間上の内積に変換することができる。また、 と仮定している（ソボレフ空間 を参照）。解の存在と一意性も示すことができる。 ∇{\displaystyle \nabla}⋅{\displaystyle \cdot}ϕ{\displaystyle \,\!\phi }H01（Ω）{\displaystyle H_{0}^{1}(\オメガ )}Ω{\displaystyle \オメガ}∂Ω{\displaystyle \partial \Omega }v∈H01（Ω）{\displaystyle v\in H_{0}^{1}(\Omega )}

解の存在と一意性の証明の概要

を、およびにおける絶対連続な関数として大まかに考えることができます（ソボレフ空間を参照）。このような関数は（弱）1回微分可能であり、対称双線型写像は内積を定義し、それがヒルベルト空間になることがわかります（詳細な証明は自明ではありません）。一方、左辺も内積であり、今回はLp 空間上にあります。ヒルベルト空間に対するリースの表現定理を適用すると、 (2)の唯一の解が存在することが示され、したがって P1 が存在します。この解は、アプリオリに の元であるだけですが、楕円正則性を使用すると、 の場合には滑らかになります。 H01（0、1）{\displaystyle H_{0}^{1}(0,1)}（0、1）{\displaystyle (0,1)}0{\displaystyle 0}×＝0{\displaystyle x=0}×＝1{\displaystyle x=1}ϕ{\displaystyle \!\,\phi }H01（0、1）{\displaystyle H_{0}^{1}(0,1)}∫01f（×）v（×）d×{\displaystyle \int _{0}^{1}f(x)v(x)dx}L2（0、1）{\displaystyle L^{2}(0,1)}あなた{\displaystyle u}H01（0、1）{\displaystyle H_{0}^{1}(0,1)}f{\displaystyle f}

離散化

端点にゼロ値を持つ関数（青）と区分線形近似（赤）H01、{\displaystyle H_{0}^{1},}

P1とP2は離散化の準備ができており、共通の部分問題(3)につながる。基本的な考え方は、無限次元線形問題を次のように置き換えることである。

次のようなものを見つけるあなた∈H01{\displaystyle u\in H_{0}^{1}}
たv∈H01、−ϕ（あなた、v）＝∫fv{\displaystyle \forall v\in H_{0}^{1},\;-\phi (u,v)=\int fv}

有限次元バージョンでは次のようになります。

ここではの有限次元部分空間である。 には多くの選択肢があり（一つの可能​​性はスペクトル法につながる）、有限要素法では を区分多項式関数の空間としてとる。 V{\displaystyle V}H01{\displaystyle H_{0}^{1}}V{\displaystyle V}V{\displaystyle V}

問題P1の場合

区間 を取り、 の値を選択し、を次のように定義します。 （0、1）{\displaystyle (0,1)}n{\displaystyle n}×{\displaystyle x}0＝×0<×1<⋯<×n<×n+1＝1{\displaystyle 0=x_{0}、x_{1}、x_{n}、x_{n+1 ...V{\displaystyle V}V＝{v:[0、1]→R:v 連続的である、 v|[×け、×け+1] は線形である け＝0、…、n、 そして v（0）＝v（1）＝0}{\displaystyle V=\{v:[0,1]\to \mathbb {R} \;:v{\text{ は連続、 }}v|_{[x_{k},x_{k+1}]}{\text{ は }}k=0,\dots ,n{\text{ に対して線形、 }}v(0)=v(1)=0\}}

ここで、 とを定義します。微積分学の基本定義によれば、 の関数は微分可能ではないことに注意してください。実際、の場合、 のどの においても の微分は定義されません。しかし、 の他のすべての値においては の微分は存在し、この微分を用いて の部分積分を行うことができます。 ×0＝0{\displaystyle x_{0}=0}×n+1＝1{\displaystyle x_{n+1}=1}V{\displaystyle V}v∈V{\displaystyle v\in V}×＝×け{\displaystyle x=x_{k}}け＝1、…、n{\displaystyle k=1,\ldots ,n}×{\displaystyle x}

2次元における区分線形関数

問題P2の場合

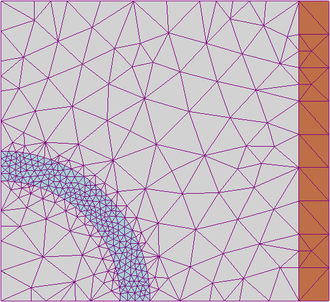
関数の集合である必要があります。右の図では、平面上の15辺の多角形領域の三角形分割（下）と、三角形分割の各三角形上で線形であるこの多角形の区分線形関数（上、カラー）を示しています。空間は、選択された三角形分割の各三角形上で線形である関数で構成されます。 V{\displaystyle V}Ω{\displaystyle \オメガ}Ω{\displaystyle \オメガ}V{\displaystyle V}

基礎となる三角形メッシュがどんどん細かくなるにつれて、離散問題(3)の解は、ある意味では、元の境界値問題P2の解に収束することが期待されます。このメッシュの細かさを測るために、三角形分割は、非常に小さいとみなされる実数値パラメータでインデックス付けされます。このパラメータは、三角形分割における三角形の最大または平均サイズに関係します。三角形分割を精緻化すると、区分線形関数の空間も とともに変化する必要があります。このため、文献では ではなく と読むことがよくあります。ここではそのような分析は行わないため、この表記法は使用しません。 h>0{\displaystyle h>0}V{\displaystyle V}h{\displaystyle h}Vh{\displaystyle V_{h}}V{\displaystyle V}

基準の選択

ベッセル関数の補間
J0を再構築するために使用された16個の三角基底関数
ゼロ次ベッセル関数J 0 (黒)を再構築するために使用される、16 個のスケールおよびシフトされた三角基底関数 (カラー)
基底関数の和
基底関数の線形結合 (黄色) は、J 0 (黒) を任意の精度で再現します。

離散化を完了するには、の基底を選択する必要があります。1次元の場合、各制御点について、の値が で、すべての でゼロとなる区分線形関数を選択します。つまり、 V{\displaystyle V}×け{\displaystyle x_{k}}vけ{\displaystyle v_{k}}V{\displaystyle V}1{\displaystyle 1}×け{\displaystyle x_{k}}×j、j≠け{\displaystyle x_{j},\;j\neq k}vけ（×）＝{×−×け−1×け−×け−1 もし ×∈[×け−1、×け]、×け+1−××け+1−×け もし ×∈[×け、×け+1]、0 さもないと、{\displaystyle v_{k}(x)={\begin{cases}{x-x_{k-1} \over x_{k}\,-x_{k-1}}&{\text{ if }}x\in [x_{k-1},x_{k}],\\{x_{k+1}\,-x \over x_{k+1}\,-x_{k}}&{\text{ if }}x\in [x_{k},x_{k+1}],\\0&{\text{ otherwise}},\end{cases}}}

に対して、この基底はシフトされスケールされたテント関数である。2次元の場合、平面領域 の三角形分割の頂点ごとに1つの基底関数を再び選択する。関数 は、における値がであり、すべての において 0 である唯一の関数である。 け＝1、…、n{\displaystyle k=1,\dots ,n}vけ{\displaystyle v_{k}}×け{\displaystyle x_{k}}Ω{\displaystyle \オメガ}vけ{\displaystyle v_{k}}V{\displaystyle V}1{\displaystyle 1}×け{\displaystyle x_{k}}×j、j≠け{\displaystyle x_{j},\;j\neq k}

「有限要素法」における「要素」という言葉は、著者によって、領域の三角形、区分線形基底関数、あるいはその両方を指します。例えば、曲線領域に関心のある著者は、三角形を曲線プリミティブに置き換え、要素を曲線であると記述するかもしれません。一方、一部の著者は「区分線形」を「区分二次式」や「区分多項式」に置き換えます。その場合、著者は「高次多項式」ではなく「高次要素」と言うかもしれません。有限要素法は三角形（3次元空間における四面体や多次元空間における高次単体）に限定されません。それでも、四辺形部分領域（3次元空間における六面体、プリズム、ピラミッドなど）上で定義できます。高次形状（曲線要素）は、多項式形状だけでなく、非多項式形状（例えば、楕円や円）でも定義できます。

高次区分多項式基底関数を使用する方法の例としては、hp-FEMとスペクトル FEMがあります。

より高度な実装（適応型有限要素法）では、結果の品質を（誤差推定理論に基づいて）評価し、連続体問題の厳密解から一定の範囲内で近似解を得ることを目指して、解の計算中にメッシュを修正する手法が用いられます。メッシュ適応には様々な手法が用いられますが、最も一般的なものは以下のとおりです。

  • 移動するノード（r適応性）
  • 精製要素（および精製されていない要素）（h適応性）
  • 基底関数の順序の変更（p適応性）
  • 上記の組み合わせ（hp-adaptivity）。

基盤の小さなサポート

境界条件がゼロで、原点を中心とし半径が 1 である円板上の2 次元問題を解きます。 (a) 三角測量。あなた××+あなたyy＝−4{\displaystyle u_{xx}+u_{yy}=-4}
(b)離散化線形システムの疎行列L
（c）計算された解、あなた（×、y）＝1−×2−y2{\displaystyle u(x,y)=1-x^{2}-y^{2}}

この基底選択の主な利点は、 と の内積 が ほぼすべての に対してゼロになることです。（の位置を含む行列はグラミアン行列として知られています。）1次元の場合、の台は区間 です。したがって、 のときは常にとの積分関数はゼロになります。 ⟨vj、vけ⟩＝∫01vjvけd×{\displaystyle \langle v_{j},v_{k}\rangle =\int _{0}^{1}v_{j}v_{k}\,dx}ϕ（vj、vけ）＝∫01vj′vけ′d×{\displaystyle \phi (v_{j},v_{k})=\int _{0}^{1}v_{j}'v_{k}'\,dx}j、け{\displaystyle j,k}⟨vj、vけ⟩{\displaystyle \langle v_{j},v_{k}\rangle }（j、け）{\displaystyle (j,k)}vけ{\displaystyle v_{k}}[×け−1、×け+1]{\displaystyle [x_{k-1},x_{k+1}]}⟨vj、vけ⟩{\displaystyle \langle v_{j},v_{k}\rangle }ϕ（vj、vけ）{\displaystyle \phi (v_{j},v_{k})}|j−k|>1{\displaystyle |j-k|>1}

同様に、平面の場合、とが三角形分割の辺を共有しない場合、積分 と 積分は 両方ともゼロになります。 xj{\displaystyle x_{j}}xk{\displaystyle x_{k}}∫Ωvjvkds{\displaystyle \int _{\Omega }v_{j}v_{k}\,ds}∫Ω∇vj⋅∇vkds{\displaystyle \int _{\Omega }\nabla v_{j}\cdot \nabla v_{k}\,ds}

問題の行列形式

と書くと、問題(3)はをとすると、 u(x)=∑k=1nukvk(x){\displaystyle u(x)=\sum _{k=1}^{n}u_{k}v_{k}(x)}f(x)=∑k=1nfkvk(x){\displaystyle f(x)=\sum _{k=1}^{n}f_{k}v_{k}(x)}v(x)=vj(x){\displaystyle v(x)=v_{j}(x)}j=1,…,n{\displaystyle j=1,\dots ,n}

列ベクトルをと で表し、 を、 を 要素が である行列 とすると 、 (4)式は次のように書き換えられる。 u{\displaystyle \mathbf {u} }f{\displaystyle \mathbf {f} }(u1,…,un)t{\displaystyle (u_{1},\dots ,u_{n})^{t}}(f1,…,fn)t{\displaystyle (f_{1},\dots ,f_{n})^{t}}L=(Lij){\displaystyle L=(L_{ij})}M=(Mij){\displaystyle M=(M_{ij})}Lij=ϕ(vi,vj){\displaystyle L_{ij}=\phi (v_{i},v_{j})}Mij=∫vivjdx{\displaystyle M_{ij}=\int v_{i}v_{j}dx}

を仮定する必要はない。一般の関数 の場合、行列が使われない ので、問題(3)は実際にはより単純になる。f(x)=∑k=1nfkvk(x){\displaystyle f(x)=\sum _{k=1}^{n}f_{k}v_{k}(x)}f(x){\displaystyle f(x)}v(x)=vj(x){\displaystyle v(x)=v_{j}(x)}j=1,…,n{\displaystyle j=1,\dots ,n}M{\displaystyle M}

ここで、および です。 b=(b1,…,bn)t{\displaystyle \mathbf {b} =(b_{1},\dots ,b_{n})^{t}}bj=∫fvjdx{\displaystyle b_{j}=\int fv_{j}dx}j=1,…,n{\displaystyle j=1,\dots ,n}

前に述べたように、基底関数の台が小さいため、と のほとんどの要素はゼロになります。したがって、逆行列を求める必要がある行列 のほとんどの要素がゼロであるような、未知数を含む線形連立方程式を解く必要があります。 L{\displaystyle L}M{\displaystyle M}vk{\displaystyle v_{k}}u{\displaystyle \mathbf {u} }L{\displaystyle L}

このような行列はスパース行列と呼ばれ、このような問題には効率的なソルバーが存在します（行列の逆行列を求めるよりもはるかに効率的です）。さらに、は対称かつ正定値行列であるため、共役勾配法などの手法が好まれます。問題がそれほど大きくない場合は、スパースLU分解やコレスキー分解も依然として有効です。例えば、MATLABのバックスラッシュ演算子（スパースLU分解、スパースコレスキー分解、その他の因数分解法を使用）は、10万頂点のメッシュに対して十分な効果を発揮します。 L{\displaystyle L}

マトリックスは通常、剛性マトリックスと呼ばれ、マトリックスは質量マトリックスと呼ばれます。 L{\displaystyle L}M{\displaystyle M}

有限要素法の一般的な形式

一般的に、有限要素法は以下のプロセスによって特徴付けられます。

  • のグリッドを選択します。これまでの処理では、グリッドは三角形で構成されていましたが、正方形や曲線の多角形を使用することもできます。Ω{\displaystyle \Omega }
  • 次に、基底関数を選択します。これまでの議論では区分線形基底関数を使用しましたが、区分多項式基底関数を使用するのが一般的です。

別途考慮すべき事項として、基底関数の滑らかさがあります。2階楕円境界値問題の場合、単に連続する区分多項式基底関数（すなわち、導関数が不連続）で十分です。高階偏微分方程式の場合は、より滑らかな基底関数を使用する必要があります。例えば、 のような4階問題では、 となる区分2次基底関数を使用できます。 uxxxx+uyyyy=f{\displaystyle u_{xxxx}+u_{yyyy}=f}C1{\displaystyle C^{1}}

もう一つの考慮事項は、上記の例における有限次元空間とその無限次元空間の関係である。適合要素法とは、空間が連続問題に対する要素空間の部分空間となるような方法である。上記の例はそのような方法である。この条件が満たされない場合、非適合要素法が得られる。その一例として、メッシュ上の各辺の中点で連続する区分線形関数の空間が挙げられる。これらの関数は一般に辺に沿って不連続であるため、この有限次元空間は元の空間の部分空間ではない。 V{\displaystyle V}H01{\displaystyle H_{0}^{1}}V{\displaystyle V}H01{\displaystyle H_{0}^{1}}

典型的には、与えられたメッシュを細分化するアルゴリズムが存在します。精度向上の主な方法がメッシュの細分化である場合、h法が用いられます（hは通常、メッシュ内の最大要素の直径です）。このように、ある および に対して、グリッドの誤差がで上界となることが示されれば、 p次法となります。特定の仮定（例えば、領域が凸である場合）の下では、 次区分多項式法は 次誤差を持ちます。 h{\displaystyle h}Chp{\displaystyle Ch^{p}}C<∞{\displaystyle C<\infty }p>0{\displaystyle p>0}d{\displaystyle d}p=d+1{\displaystyle p=d+1}

h を小さくする代わりに、基底関数に用いる多項式の次数を上げると、p法となります。これら2種類の改良法を組み合わせると、hp法（hp-FEM ）となります。hp-FEMでは、多項式の次数は要素ごとに変化します。大きな均一なpを持つ高次法は、スペクトル有限要素法（ SFEM ）と呼ばれます。これらはスペクトル法と混同しないでください。

ベクトル偏微分方程式の場合、基底関数は の値を取ることがあります。 Rn{\displaystyle \mathbb {R} ^{n}}

さまざまな種類の有限要素法

AEM

応用要素法 (AEM) は、FEM と離散要素法(DEM) の両方の機能を組み合わせたものです。

A-FEM

Yang 氏と Lui 氏は拡張有限要素法を導入しました。その目的は、PuM 氏が述べたように、追加の自由度を必要とせずに弱い不連続性と強い不連続性をモデル化することです。

カットFEM

カット有限要素アプローチは2014年に開発されました。[ 16 ]このアプローチは、「標準的な有限要素法の精度と堅牢性を維持しながら、離散化を幾何学的記述から可能な限り独立させ、メッシュ生成の複雑さを最小限に抑えること」を目的としています。[ 17 ]

一般化有限要素法

一般化有限要素法（GFEM）は、必ずしも多項式ではない関数からなる局所空間を用いて、未知解に関する利用可能な情報を反映し、良好な局所近似を保証する。次に、これらの空間を1の分割によって「結合」し、近似部分空間を形成する。GFEMの有効性は、複雑な境界を持つ領域、マイクロスケールの問題、境界層の問題に適用した場合に実証されている。[ 18 ]

混合有限要素法

混合有限要素法は、偏微分方程式の問題を離散化する際に追加の独立変数が節点変数として導入される有限要素法の一種です。

変数 – 多項式

hp -FEMは、可変サイズhと多項式次数pを持つ要素を適応的に組み合わせることで、非常に高速な指数収束率を実現します。[ 19 ]

hpk-FEM

hpk -FEM は、可変サイズh、局所近似の多項式次数p、および局所近似のグローバル微分可能性 ( k -1) を持つ要素を適応的に組み合わせて、最高の収束率を実現します。

有限要素法

拡張有限要素法（XFEM）は、一般化有限要素法（GFEM）と単位の分割法（PUM）に基づく数値解析手法です。不連続関数を含む微分方程式の解の解空間を拡張することで、従来の有限要素法を拡張します。拡張有限要素法は、近似空間を拡張することで、対象の問題に関連する難しい特徴（不連続性、特異点、境界層など）を自然に再現します。問題によっては、このような問題の特徴を近似空間に埋め込むことで、収束速度と精度が大幅に向上することが示されています。さらに、不連続性を含む問題をXFEMで扱うことで、不連続面のメッシュ作成と再メッシュ作成の必要性が抑えられ、不連続性をメッシュエッジに制限するという代償を払うことで、従来の有限要素法に関連する計算コストと投影誤差が軽減されます。

いくつかの研究コードでは、この手法をさまざまな程度に実装しています。

  1. ゲットFEM++
  2. xfem++
  3. オープンXFEM++

XFEMは、Altair Radios、ASTER、Morfeo、Abaqusなどのコードにも実装されています。他の商用有限要素ソフトウェアにも採用が進んでおり、いくつかのプラグインと実際のコア実装が利用可能です（ANSYS、SAMCEF、OOFELIEなど）。

スケール境界有限要素法（SBFEM）

スケール境界有限要素法（SBFEM）は、SongとWolf（1997）によって導入されました。[ 20 ] SBFEMは、破壊力学問題の数値解析分野において最も有益な貢献の一つとなっています。これは、有限要素法の定式化と手順、そして境界要素の離散化の利点を組み合わせた、半解析的な基礎解を必要としない手法です。しかし、境界要素法とは異なり、基礎微分解は不要です。

S-FEM

S-FEM（平滑化有限要素法）は、物理現象のシミュレーションのための数値シミュレーションアルゴリズムの一種です。メッシュフリー法と有限要素法を組み合わせることで開発されました。

スペクトル要素法

スペクトル要素法は、有限要素法の幾何学的柔軟性とスペクトル法の優れた精度を組み合わせたものである。スペクトル法は、高次ラグランジュ補間に基づく弱形式偏方程式の近似解であり、特定の求積法則のみを用いて用いられる。[ 21 ]

メッシュフリー法

不連続ガラーキン法

有限要素極限解析

ストレッチグリッド法

ルビニャック反復法

ルビニャック反復法は有限要素法における反復法です。

結晶塑性有限要素法（CPFEM）

結晶塑性有限要素法（CPFEM）は、フランツ・ローターズによって開発された高度な数値解析ツールです。金属は結晶の集合体とみなすことができ、変形時に異常な応力やひずみの局所化など、異方性を示します。CPFEMは、すべり（せん断ひずみ速度）に基づいて、転位、結晶方位、その他の組織情報を計算することで、日常的な解析において結晶異方性を考慮することができます。CPFEMは、材料の変形、表面粗さ、破壊などの数値解析に応用されています。

仮想要素法（VEM）

仮想要素法（VEM）は、Beirão da Veigaら（2013）[ 22 ]によって、擬似差分法（MFD）の拡張として導入され、任意の要素形状に対する標準的な有限要素法の一般化である。これにより、非常に不規則で非凸な形状を持つ一般的な多角形（3次元では多面体）を扱えるようになる。 「仮想」という名称は、局所的な形状関数の基底に関する知識が不要であり、実際には明示的に計算されることがないことから由来している。

いくつかの種類の有限要素法（適合有限要素法、非適合有限要素法、混合有限要素法）は、勾配離散化法（GDM）の特殊なケースです。したがって、一連の問題（線形および非線形楕円問題、線形、非線形、および退化した放物線問題）に対して確立されているGDMの収束特性は、これらの特定の有限要素法にも当てはまります。

差分法との比較

有限差分法（FDM）は、偏微分方程式の解を近似する別の方法です。FEMとFDMの違いは以下のとおりです。

  • FEMの最大の魅力は、複雑な形状（および境界）を比較的容易に扱えることです。FDMの基本形態は長方形とその単純な変形に限定されていますが、FEMにおける形状の扱いは理論的には簡単です。[ 3 ] [ 23 ]
  • FDMは通常、不規則なCAD形状には使用されず、長方形またはブロック状のモデルに使用されることが多い。[ 24 ]
  • FEMは一般的にFDMよりも柔軟なメッシュ適応性を可能にする。[ 23 ]
  • 有限差分法の最も魅力的な特徴は、実装が簡単なことである。[ 23 ]
  • FDMはFEMアプローチの特殊なケースとしていくつかの観点から考えられます。例えば、問題が正方長方形メッシュで離散化され、各長方形が2つの三角形に分割されている場合、1次FEMはポアソン方程式のFDMと同一です。
  • たとえば、FDM ではグリッド ポイント間の近似の品質が低いため、有限要素近似の数学的基礎がより健全であると考える理由があります。
  • FEM 近似の品質は、対応する FDM アプローチよりも高い場合が多いですが、これは問題に大きく依存し、逆の例もいくつかあります。

一般的に、FEMは構造力学におけるあらゆるタイプの解析（固体の変形や応力、構造物のダイナミクスの解析など）において最適な手法です。一方、数値流体力学（CFD）では、FDMや有限体積法（FVM）などの手法が用いられる傾向があります。CFDの問題は通常、問題を多数のセル／グリッドポイント（数百万以上）に離散化する必要があります。そのため、解のコストを考えると、各セル内ではより単純で低次の近似が有利です。これは特に、自動車や飛行機の周囲の気流、気象シミュレーションなどの「外部流れ」の問題に当てはまります。

有限要素法と高速フーリエ変換（FFT）法

偏微分方程式の解を近似する別の方法は高速フーリエ変換(FFT) であり、この方法では解は FFT を使用して計算されたフーリエ級数によって近似されます。応力を受ける材料の機械的応答を近似する場合、FFT の方がはるかに高速であることが多いですが[ 25 ]、FEM の方が正確な場合があります[ 26 ] 。 2 つの方法それぞれの利点の 1 つの例は、アルミニウム(FCC 金属)のシートの圧延とタングステン(BCC 金属)のワイヤの描画のシミュレーションです。このシミュレーションには、FFT 法用の高度な形状更新アルゴリズムがありませんでした。どちらの場合も、FFT 法は FEM よりも 10 倍以上高速でしたが、結晶粒が大きく変形するワイヤの描画シミュレーションでは、FEM 法の方がはるかに正確でした。シート圧延シミュレーションでは、2 つの方法の結果は類似していました。[ 26 ] FFTは、境界条件が材料のひずみで与えられる場合には速度面で大きな利点があるが、応力を用いて境界条件を適用する場合には、より多くの反復計算が必要となるため、その効率はいくらか低下する。[ 27 ]

FE法とFFT法は、ボクセルベースの手法(2)で組み合わせて材料の変形をシミュレートすることもできます。この手法では、FE法はマクロスケールの応力と変形に使用され、FFT法はマイクロスケールで使用され、マイクロスケールが機械的応答に与える影響を扱います。[ 28 ] FEMとは異なり、FFT法は画像処理手法に類似しているため、顕微鏡で撮影した実際の微細構造画像をソルバーに入力して、より正確な応力応答を得ることができます。FFTで実際の画像を使用すると、微細構造のメッシュ分割を回避できます。メッシュ分割は、微細構造のFEMシミュレーションを使用する場合に必要であり、困難な場合があります。フーリエ近似は本質的に周期的であるため、FFTは周期的な微細構造の場合にのみ使用できますが、これは実際の材料では一般的です。[ 28 ] FFTは、フーリエ成分を変分基底として要素内のフィールドを近似することで、FEM法と組み合わせることもできます。これにより、FFTベースのソルバーの速度を活用できます。[ 29 ]

応用

3D汚染輸送モデル - 地上レベルの濃度場
3D汚染輸送モデル - 垂直面上の濃度場

機械工学分野に属する様々な専門分野（航空、生体力学、自動車産業など）では、製品の設計・開発において統合FEMが一般的に使用されています。最新のFEMパッケージの中には、熱、電磁気、流体、構造といった特定の作業環境要素を組み込んだものもあります。構造シミュレーションにおいて、FEMは剛性と強度の可視化、重量、材料、コストの最小化に大きく貢献します。[ 30 ]

人間の膝関節の有限要素モデル[ 31 ]

この強力な設計ツールは、多くの産業用途において、エンジニアリング設計の基準と設計プロセス方法論の両方を大幅に改善しました。[ 32 ] FEMの導入により、製品を構想から生産ラインに出すまでの時間が大幅に短縮されました。[ 32 ]テストと開発は、主にFEMを使用した初期プロトタイプ設計の改善を通じて加速されました。[ 33 ]まとめると、FEMの利点には、精度の向上、設計の強化、重要な設計パラメータへの洞察の向上、仮想プロトタイピング、ハードウェアプロトタイプの削減、設計サイクルの迅速化とコスト削減、生産性の向上、収益の増加などがあります。[ 32 ]

1990年代には、FEMは確率モデルを数値的に解くための確率論的モデリングに使用するために提案され[ 34 ]、その後、信頼性評価にも使用されるようになりました[ 35 ] 。

FEMは、物理系を記述する微分方程式の近似に広く応用されています。この手法は計算流体力学の分野で非常に人気があり、ナビエ・ストークス方程式をFEMで解く例も数多くあります。[ 36 ] [ 37 ] [ 38 ]近年、計算プラズマ研究におけるFEMの応用が増加しています。FEMを用いた磁気流体力学、ヴラソフ方程式、シュレーディンガー方程式の有望な数値解析結果が提案されています。[ 39 ] [ 40 ]

参照

参考文献

  1. ^ Hoang, Viet Ha; Schwab, Christoph (2005). 「多重スケール楕円問題のための高次元有限要素法」.マルチスケールモデリング＆シミュレーション. 3 (1). SIAM: 168– 194. doi : 10.1137/030601077 . hdl : 20.500.11850/147656 .
  2. ^ Daryl L. Logan (2011).有限要素法入門コース. Cengage Learning. ISBN 978-0-495-66827-5。
  3. ^ a b Reddy, JN (2006).有限要素法入門（第3版）. McGraw-Hill. ISBN 978-0-07-126761-8。
  4. ^「編集委員会」.有限要素法による解析と設計. 211 103845. 2022. doi : 10.1016/s0168-874x(22)00118-4 . ISSN 0168-874X . 
  5. ^ Huebner, Kenneth H. (2001).エンジニアのための有限要素法. Wiley. ISBN 978-0-471-37078-9。
  6. ^ Liu, Wing Kam; Li, Shaofan; Park, Harold S. (2022). 「有限要素法の80年：誕生、進化、そして未来」 .工学計算手法アーカイブ. 29 (6): 4431– 4453. arXiv : 2107.04960 . doi : 10.1007/s11831-022-09740-9 . ISSN 1134-3060 . S2CID 235794921 .  
  7. ^レンニコフ、アレクサンダー (1941). 「フレームワーク法による弾性問題の解法」応用力学ジャーナル. 8 (4): 169– 175. Bibcode : 1941JAM.....8A.169H . doi : 10.1115/1.4009129 .
  8. ^ Courant, R. (1943). 「平衡と振動の問題を解くための変分法」アメリカ数学会報. 49 (1): 1– 23. doi : 10.1090/s0002-9904-1943-07818-4 .
  9. ^ "СПб ЭМИ РАН" . emi.nw.ru. 2015年9月30日時点のオリジナルよりアーカイブ。2018年3月17日閲覧。
  10. ^ Hinton, Ernest; Irons, Bruce (1968年7月). 「有限要素法を用いた実験データの最小二乗平滑化」. Strain . 4 (3): 24– 27. doi : 10.1111/j.1475-1305.1968.tb01368.x .
  11. ^ 「SAP-IVソフトウェアとマニュアル」。NISEE e-Library、地震工学オンラインアーカイブ。2013年3月9日時点のオリジナルよりアーカイブ。 2013年1月24日閲覧。
  12. ^ガード・ポールセン;ホーコンとアンデルセン。ジョン・ペッター・コレット;イヴェール・タンゲン・ステンスラッド（2014）。信頼の構築、DNV の歴史 1864 ～ 2014。ライサケル、ノルウェー: Dinamo Forlag A/S. 121、436ページ。ISBN 978-82-8071-256-1。
  13. ^ストラング、ギルバート、フィックス、ジョージ(1973).有限要素法の分析. プレンティス・ホール. ISBN 978-0-13-032946-2。
  14. ^ Olek C Zienkiewicz、Robert L Taylor、JZ Zhu (2013年8月31日).有限要素法：その基礎と原理. Butterworth-Heinemann. ISBN 978-0-08-095135-5。
  15. ^ Bathe, KJ (2006).有限要素法の手順. Cambridge, MA: Klaus-Jürgen Bathe. ISBN 978-0-9790049-0-2。
  16. ^ celledoni (2023年2月27日). 「CutFEM: 偏微分方程式と幾何学の離散化」 . ECMI . 2023年10月13日閲覧。
  17. ^ Burman, Erik; Claus, Susanne; Hansbo, Peter; Larson, Mats G.; Massing, André (2015-11-16). 「CutFEM: 幾何学と偏微分方程式の離散化」 . International Journal for Numerical Methods in Engineering . 104 (7): 472– 501. Bibcode : 2015IJNME.104..472B . doi : 10.1002/nme.4823 . ISSN 0029-5981 . 
  18. ^ Babuška, Ivo ; Banerjee, Uday; Osborn, John E. (2004年6月). 「一般化有限要素法：主要な考え方、結果、そして展望」. International Journal of Computational Methods . 1 (1): 67– 103. doi : 10.1142/S0219876204000083 .
  19. ^ P. ソリン、K. セゲス、I. ドレーゼル：高次有限要素法、チャップマン＆ホール/CRCプレス、2003年
  20. ^ Song, Chongmin; Wolf, John P. (1997年8月5日). 「弾性力学のためのスケール境界有限要素法（別名コンシステント無限小有限要素セル法）」 .応用力学・工学におけるコンピュータ手法. 147 ( 3–4 ): 329– 355. Bibcode : 1997CMAME.147..329S . doi : 10.1016/S0045-7825(97)00021-2 .
  21. ^ 「スペクトル要素法」国家科学技術計算重点研究室. 2017年8月10日時点のオリジナルよりアーカイブ。 2017年7月28日閲覧。
  22. ^ Beirão da Veiga, L.; Brezzi, F.; Cangiani, A.; Manzini, G.; Marini, LD; Russo, A. (2013). 「仮想要素法の基本原理」.応用科学における数学モデルと手法. 23 (1): 199– 214. Bibcode : 2013M3AS...23..199B . doi : 10.1142/S0218202512500492 .
  23. ^ a b c Topper, Jürgen (2005年1月). 「有限要素法によるオプション価格設定」. Wilmott . 2005 (1): 84–90 . doi : 10.1002/wilm.42820050119 (2026年1月15日現在非アクティブ). ISSN 1540-6962 . {{cite journal}}: CS1 maint: DOI inactive as of January 2026 (link)
  24. ^ 「FEM、FDM、FVMの違いとは？」 . Machine Design . 2016年4月18日. 2017年7月28日時点のオリジナルよりアーカイブ。 2017年7月28日閲覧。
  25. ^ Ma, X; Parvathaneni, K; Lomov, S; Vasiukov, D; Shakoor, M; Park, C (2019年12月). 「複合材料のマイクロメカニカルモデリングにおける高速フーリエ変換と有限要素法の定量的比較」 FiBreMoDカンファレンス.
  26. ^ a b Prakash, A; Lebensohn, RA (2009-09-01). 「多結晶のマイクロメカニクス挙動のシミュレーション：有限要素法と高速フーリエ変換」 .材料科学と工学におけるモデリングとシミュレーション. 17 (6) 064010. Bibcode : 2009MSMSE..17f4010P . doi : 10.1088/0965-0393/17/6/064010 . ISSN 0965-0393 . 
  27. ^ Cruzado, A; Segurado, J; Hartl, DJ; Benzerga, AA (2021-06-01). 「相転移材料のための変分高速フーリエ変換法」 .材料科学と工学におけるモデリングとシミュレーション. 29 (4): 045001. Bibcode : 2021MSMSE..29d5001C . doi : 10.1088/1361-651X/abe4c7 . ISSN 0965-0393 . 
  28. ^ a b Gierden, Christian; Kochmann, Julian; Waimann, Johanna; Svendsen, Bob; Reese, Stefanie (2022-10-01). 「微細構造の発達とマクロスコピックな材料挙動の計算モデリングにおけるFE-FFTベースの2スケール法のレビュー」 .工学計算手法アーカイブ. 29 (6): 4115– 4135. doi : 10.1007/s11831-022-09735-6 . ISSN 1886-1784 . 
  29. ^ Zeman, J.; de Geus, TWJ; Vondřejc, J.; Peerlings, RHJ; Geers, MGD (2017-09-07). 「非線形FFTベースのマイクロメカニクスシミュレーションにおける有限要素法の視点：非線形FFTベースのシミュレーションにおける有限要素法の視点」 . International Journal for Numerical Methods in Engineering . 111 (10): 903– 926. arXiv : 1601.05970 . doi : 10.1002/nme.5481 .
  30. ^ Kiritsis, D.; Eemmanouilidis, Ch.; Koronios, A.; Mathew, J. (2009). 「エンジニアリングアセットマネジメント」.第4回世界エンジニアリングアセットマネジメント会議 (WCEAM) 議事録: 591–592 .
  31. ^ Naghibi Beidokhti, Hamid; Janssen, Dennis; Khoshgoftar, Mehdi; Sprengers, Andre; Perdahcioglu, Emin Semih; Boogaard, Ton Van den; Verdonschot, Nico (2016). 「ネイティブ膝関節の動的暗黙法と明示法による有限要素シミュレーションの比較」(PDF) . Medical Engineering & Physics . 38 (10): 1123– 1130. doi : 10.1016/j.medengphy.2016.06.001 . PMID 27349493. 2018年7月19日時点のオリジナルよりアーカイブ(PDF) . 2019年9月19日閲覧. 
  32. ^ a b c Hastings, JK, Juds, MA, Brauer, JR、「有限要素磁気解析の精度と経済性」、第33回全国リレー会議、1985年4月。
  33. ^マクラーレン・メルセデス (2006). 「マクラーレン・メルセデス：特集 - 印象に残るストレス」 2006年10月30日時点のオリジナルよりアーカイブ。 2006年10月3日閲覧。
  34. ^ Peng Long; Wang Jinliang; Zhu Qiding (1995年5月19日). 「有限要素確率計算のための高精度手法」. Journal of Computational and Applied Mathematics . 59 (2): 181– 189. doi : 10.1016/0377-0427(94)00027-X .
  35. ^ Haldar, Achintya; Mahadevan, Sankaran (2000).確率的有限要素解析を用いた信頼性評価. John Wiley & Sons. ISBN 978-0-471-36961-5。
  36. ^ Girault, Vivette; Raviart, Pierre-Arnaud (1979).ナビエ・ストークス方程式の有限要素近似. 第749巻. Springer Berlin. ISBN 978-3-540-09557-6。
  37. ^キュベリエ、コルネリス;シーガル、8月。ヴァン・スティーンホーフェン、アントン・A (1986)。有限要素法とナビエ・ストークス方程式。 Vol. 22. シュプリンガーサイエンス＆ビジネスメディア。ISBN 978-1-4020-0309-7。
  38. ^ Girault, Vivette; Raviart, Pierre-Arnaud (2012).ナビエ・ストークス方程式の有限要素法：理論とアルゴリズム. 第5巻. Springer Science & Business Media. ISBN 978-3-642-64888-5。
  39. ^ Karakashian, Ohannes; Makridakis, Charalambos (1999). 「非線形シュレーディンガー方程式のための空間時間有限要素法：連続ガラーキン法」. SIAM Journal on Numerical Analysis . 36 (6). SIAM: 1779– 1807. doi : 10.1137/S0036142997330111 .
  40. ^ Sovinec, Carl R.; Glasser, AH; Gianakon, TA; Barnes, DC; Nebel, RA; Kruger, SE; Schnack, DD; Plimpton, SJ; Tarditi, A.; Chu, MS (2004). 「高次有限要素法を用いた非線形磁気流体力学シミュレーション」. Journal of Computational Physics . 195 (1). Elsevier: 355– 386. Bibcode : 2004JCoPh.195..355S . doi : 10.1016/j.jcp.2003.10.004 .

さらに読む

ウィキメディア コモンズには、有限要素モデリングに関連するメディアがあります。
「 https://en.wikipedia.org/w/index.php?title=有限要素法&oldid =1334033561」より取得