微分

黒で描かれた関数のグラフと、そのグラフの接線が赤で描かれています。接線の傾きは、マークされた点における関数の微分に等しくなります

微分可能関数の異なる点における導関数。この場合、導関数は に等しい。${\displaystyle \sin \left(x^{2}\right)+2x^{2}\cos \left(x^{2}\right)}$

数学において、導関数は関数の入力に対する出力の変化に対する感度を定量化する基本的なツールです。ある入力値における単一変数関数の導関数は、存在する場合、その点における関数のグラフの接線の傾きです。接線は、その入力値付近における関数の最良の線形近似です。導関数は、しばしば瞬間変化率、つまり従属変数の瞬間変化と独立変数の瞬間変化の比として説明されます。^{[ 1 ]}導関数を求めるプロセスは微分と呼ばれます。

微分には複数の表記法があります。ゴットフリート・ヴィルヘルム・ライプニッツにちなんで名付けられたライプニッツ表記法は、2つの微分値の比として表されます。一方、プライム表記法は、プライム記号を付して書きます。高次の表記法は繰り返し微分を表し、通常、ライプニッツ表記法では微分値に上付き文字を付して、プライム表記法ではさらにプライム記号を付して表します。高次の導関数は物理学で使用されます。例えば、運動する物体の位置の時間に関する1次導関数はその速度であり、2次導関数はその加速度です。

微分は、複数の実変数の関数に一般化できます。この場合、微分は線型変換として再解釈され、そのグラフは（適切な変換後）元の関数のグラフの最良の線型近似となります。ヤコビ行列は、独立変数と従属変数の選択によって与えられた基底に関して、この線型変換を表す行列です。これは、独立変数に関する偏微分によって計算できます。複数の変数の実数値関数の場合、ヤコビ行列は勾配ベクトルに簡約されます。

定義

限界として

実変数の関数が 定義域の点で微分可能であるとは、その定義域に⁠ ⁠を含む開区間が含まれ、かつ極限 が存在することを意味する。^{[ 2 ]} これは、任意の正の実数⁠ ⁠に対して、 となる正の実数が存在し、となる任意の正の実数に対してが定義され、 縦棒は絶対値 を表すことを意味する。これは極限 の (ε, δ)-定義の例である。^{[ 3 ]}${\displaystyle f(x)}$ ${\displaystyle a}$ ${\displaystyle a}$ $${\displaystyle L=\lim_{h\to 0}{\frac{f(a+h)-f(a)}{h}}}$$ ${\displaystyle \varepsilon}$ ${\displaystyle \delta}$ ${\displaystyle h}$ ${\displaystyle |h|<\delta}$ ${\displaystyle h\neq 0}$ ${\displaystyle f(a+h)}$ $${\displaystyle \left|L-{\frac {f(a+h)-f(a)}{h}}\right|<\varepsilon,}$$

関数が⁠ ⁠で微分可能、つまり極限が存在する場合、この極限はにおけるの導関数と呼ばれます。 導関数の表記法は複数存在します。^{[ 4 ]}における の導関数は⁠ ⁠と表記して「⁠ ⁠の素数」と読むことも、 ⁠ ⁠と表記して「 ⁠ ⁠における⁠ ⁠に関するの導関数」または「 ⁠ ⁠ による（または⁠ ⁠上の） ⁠ ⁠による」と読むこともできます。以下の§ 表記法を参照してください。 が定義域のすべての点で導関数を持つ関数である場合、すべての点を における の導関数の値にマッピングすることによって関数を定義できます。この関数は と書かれ、 ⁠ ⁠の導関数と呼ばれます。関数は定義域の最大で導関数を持つ場合がありますが、すべての点で持つとは限りません。 が定義され、他の場所では定義されていない場合ににおける値が等しい関数は、⁠ ⁠の導関数とも呼ばれます。これは関数ではあるが、その定義域は の定義域よりも小さくなる可能性がある。^{[ 5 ]}${\displaystyle f}$ ${\displaystyle a}$ ${\displaystyle L}$ ${\displaystyle f}$ ${\displaystyle a}$ ${\displaystyle f}$ ${\displaystyle a}$ ${\displaystyle f'(a)}$ ${\displaystyle f}$ ${\displaystyle a}$ ${\displaystyle \textstyle {\frac {df}{dx}}(a)}$ ${\displaystyle f}$ ${\displaystyle x}$ ${\displaystyle a}$ ${\displaystyle df}$ ${\displaystyle dx}$ ${\displaystyle a}$ ${\displaystyle f}$ ${\displaystyle x}$ ${\displaystyle f}$ ${\displaystyle x}$ ${\displaystyle f'}$ ${\displaystyle f}$ ${\displaystyle f}$ ${\displaystyle a}$ ${\displaystyle f'(a)}$ ${\displaystyle f'(a)}$ ${\displaystyle f}$ ${\displaystyle f}$

例えば、 を二乗関数とします。すると、 の導関数の定義における商は^{[ 6 ]}です 。最後のステップの除算は である限り有効です。 が⁠ ⁠に近づくほど、この式は値 に近づきます。 極限が存在し、すべての入力に対して極限は です。したがって、二乗関数の導関数は⁠ ⁠です。 ${\displaystyle f}$ ${\displaystyle f(x)=x^{2}}$ $${\displaystyle {\frac {f(a+h)-f(a)}{h}}={\frac {(a+h)^{2}-a^{2}}{h}}={\frac {a^{2}+2ah+h^{2}-a^{2}}{h}}=2a+h.}$$ ${\displaystyle h\neq 0}$ ${\displaystyle h}$ ${\displaystyle 0}$ ${\displaystyle 2a}$ ${\displaystyle a}$ ${\displaystyle 2a}$ ${\displaystyle f'(x)=2x}$

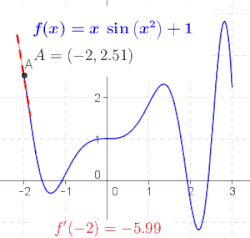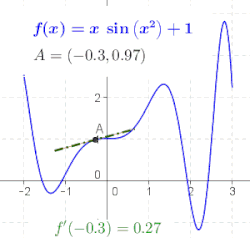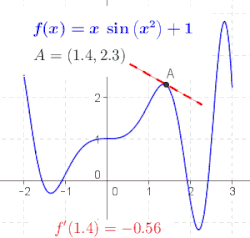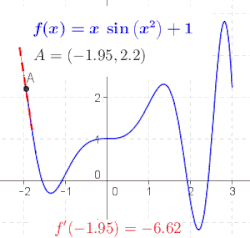
微分の定義における比は、関数⁠ ⁠${\displaystyle f}$ のグラフ上の2点、具体的には点とを通る直線の傾きです。を小さくすると、これらの点は互いに近づき、この直線の傾きは極限値、つまりにおける のグラフの接線の傾きに近づきます。言い換えれば、微分は接線の傾きです。^{[ 7 ]}${\displaystyle (a,f(a))}$ ${\displaystyle (a+h,f(a+h))}$ ${\displaystyle h}$ ${\displaystyle f}$ ${\displaystyle a}$

無限小数の使用

微分を考える一つの方法は、関数の出力の無限小変化と入力の無限小変化の比として考えることです。 ^{[ 8 ]}この直感を厳密にするために、無限小量を操作するための規則体系が必要です。^{[ 9 ]}超実数体系は、無限量と無限小量を扱う方法です。超実数は、任意の有限個の項に対しての形のどの数よりも大きい数を含む実数の拡張です。そのような数は無限であり、その逆数は無限小です。超実数を微積分学の基礎に適用することを非標準解析と呼びます。これは、微分や積分などの微積分学の基本概念を無限小数で定義する方法を提供し、それによってライプニッツ記法の に正確な意味を与えますしたがって、任意の無限小⁠ ⁠に対しての導関数は、となり、これは標準的な部分関数を表し、各有限超実数を最も近い実数に「切り捨てる」。^{[ 10 ]}再び2乗関数を例に挙げると、 ${\textstyle {\frac {df}{dx}}(a)}$ ${\displaystyle f}$ ${\displaystyle 1+1+\cdots +1}$ ${\displaystyle d}$ ${\displaystyle f(x)}$ $${\displaystyle f'(x)=\operatorname {st} \left({\frac {f(x+dx)-f(x)}{dx}}\right)}$$ ${\displaystyle dx}$ ${\displaystyle \operatorname {st} }$ ${\displaystyle f(x)=x^{2}}$ $${\displaystyle {\begin{aligned}f'(x)&=\operatorname {st} \left({\frac {x^{2}+2x\cdot dx+(dx)^{2}-x^{2}}{dx}}\right)\\&=\operatorname {st} \left({\frac {2x\cdot dx+(dx)^{2}}{dx}}\right)\\&=\operatorname {st} \left({\frac {2x\cdot dx}{dx}}+{\frac {(dx)^{2}}{dx}}\right)\\&=\operatorname {st} \left(2x+dx\right)\\&=2x.\end{aligned}}}$$

連続性と微分可能性

この関数は、マークされた点において連続ではないため（具体的には、ジャンプ不連続性があるため）、導関数を持ちません

絶対値関数は連続ですが、接線の傾きが左からと右からでは同じ値に近づかないため、x = 0で微分できません。

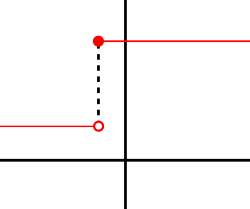
が⁠ ⁠で微分可能な場合、 は においても連続でなければなりません。^{[ 11 ]}例として、点を選び、を ⁠ ⁠未満のすべての場合に値 1 を返し、 以上のすべての場合に異なる値 10 を返すステップ関数とします。この関数はにおいて導関数を持つことができません。が負の場合、 はステップの低い部分にあるため、 からへの割線は非常に急勾配になります。 が0 に近づくにつれて、傾きは無限大に近づきます。が正の場合、 はステップの高い部分にあるため、 からへの割線の傾きは 0 になります。その結果、割線はどの傾きにも近づかないため、差分商の極限は存在しません。ただし、関数がある点で連続していても、そこでは微分可能でない場合があります。たとえば、によって与えられる絶対値関数は⁠ ⁠で連続ですが、そこでは微分可能ではありません。が正の場合、0 から への割線の傾きは1 です。が負の場合、 からへの割線の傾きは⁠ ⁠です。^{[ 12 ]} これは、 におけるグラフの「屈曲点」または「尖点」として図的に確認できます。滑らかなグラフを持つ関数であっても、その接線が垂直な点では微分可能ではありません。たとえば、 で与えられる関数は では微分可能ではありません。まとめると、導関数を持つ関数は連続ですが、導関数を持たない連続関数も存在します。^{[ 13 ]}${\displaystyle f}$ ${\displaystyle a}$ ${\displaystyle f}$ ${\displaystyle a}$ ${\displaystyle a}$ ${\displaystyle f}$ ${\displaystyle x}$ ${\displaystyle a}$ ${\displaystyle x}$ ${\displaystyle a}$ ${\displaystyle f}$ ${\displaystyle a}$ ${\displaystyle h}$ ${\displaystyle a+h}$ ${\displaystyle a}$ ${\displaystyle a+h}$ ${\displaystyle h}$ ${\displaystyle h}$ ${\displaystyle a+h}$ ${\displaystyle a}$ ${\displaystyle a+h}$ ${\displaystyle f(x)=|x|}$ ${\displaystyle x=0}$ ${\displaystyle h}$ ${\displaystyle h}$ ${\displaystyle h}$ ${\displaystyle 0}$ ${\displaystyle h}$ ${\displaystyle -1}$ ${\displaystyle x=0}$ ${\displaystyle f(x)=x^{1/3}}$ ${\displaystyle x=0}$

実際に登場するほとんどの関数は、すべての点、またはほぼすべての点で微分可能です。微積分学の歴史の初期には、多くの数学者が連続関数はほとんどの点で微分可能であると仮定していました。^{[ 14 ]}緩い条件下（たとえば、関数が単調関数またはリプシッツ関数である場合）では、これは当てはまります。しかし、1872 年にワイエルシュトラスは、どこでも連続であるがどこでも微分不可能な関数の最初の例を発見しました。この例は現在、ワイエルシュトラス関数として知られています。^{[ 15 ]} 1931 年に、シュテファン・バナッハは、ある点で導関数を持つ関数の集合は、すべての連続関数の空間において貧弱な集合であることを証明しました。非公式には、これは、ランダムな連続関数が 1 点でも導関数を持つことはほとんどないことを意味します。^{[ 16 ]}

表記法

関数の微分を表す一般的な方法の1つは、1675年にゴットフリート・ヴィルヘルム・ライプニッツによって導入されたライプニッツ表記法です。これは、微分を2つの微分（例：と）の商として表します。^{[ 17 ]}方程式を従属変数と独立変数間の関数関係と見なす場合、現在でも一般的に使用されています。1次微分は で表され、 「のに関するの微分」と読みます。 [ ^{18 ]この}微分は、関数への微分演算子の適用として扱うこともできます。高次の微分は の次微分の表記法を使用して表されます。これらは、微分演算子の複数の適用を表す略語です。たとえば、^{[ 19 ]}いくつかの代替表記法とは異なり、ライプニッツ表記法では、微分する変数を分母に明示的に指定するため、複数の関連する量を扱う際の曖昧さが排除されます合成関数の微分は連鎖律^を使って表すことができる：^[ 20 ^]${\displaystyle dy}$ ${\displaystyle dx}$ ${\displaystyle y=f(x)}$ ${\displaystyle \textstyle {\frac {dy}{dx}}}$ ${\displaystyle y}$ ${\displaystyle x}$ ${\textstyle {\frac {dy}{dx}}={\frac {d}{dx}}f(x).}$ ${\textstyle {\frac {d^{n}y}{dx^{n}}}}$ ${\displaystyle n}$ ${\displaystyle y=f(x)}$ ${\textstyle {\frac {d^{2}y}{dx^{2}}}={\frac {d}{dx}}{\Bigl (}{\frac {d}{dx}}f(x){\Bigr )}.}$ ${\displaystyle u=g(x)}$ ${\displaystyle y=f(g(x))}$ ${\textstyle {\frac {dy}{dx}}={\frac {dy}{du}}\cdot {\frac {du}{dx}}.}$

微分法のもう1つの一般的な表記法は、関数⁠ ⁠の記号にプライム記号を使用することです。この表記法は、ジョゼフ＝ルイ・ラグランジュによって考案されたもので、現在ではプライム表記法として知られています。^{[ 21 ]} 1次導関数は⁠ ⁠と書かれ、「 ⁠ ⁠の⁠ ⁠素数」と読み、 ⁠ ⁠と書かれ、「⁠ ⁠プライム」と読みます。^{[ 22 ]}同様に、2次導関数と3次導関数はそれぞれ、 ⁠ ⁠と書かれます。^{[ 23 ]}この点を超える高次の導関数の個数を示すために、著者によっては上付きローマ数字を使用する一方、または⁠ ⁠のように括弧内に数字を置く人もいます。^{[ 24 ]}後者の表記法は一般化して、 ⁠ ⁠の⁠ ⁠導関数の表記法になります。^{[ 19 ]}${\displaystyle f(x)}$ ${\displaystyle f'(x)}$ ${\displaystyle f}$ ${\displaystyle x}$ ${\displaystyle y'}$ ${\displaystyle y}$ ${\displaystyle f''}$ ${\displaystyle f'''}$ ${\displaystyle f^{\mathrm {iv} }}$ ${\displaystyle f^{(4)}}$ ${\displaystyle f^{(n)}}$ ${\displaystyle n}$ ${\displaystyle f}$

ニュートン記法またはドット記法では、時間微分を表すために記号の上にドットが置かれます。 が⁠ ⁠の関数である場合、1次および2次微分はそれぞれ⁠ ⁠と⁠ ⁠と表記できます。この記法は、時間または弧の長さに関する微分にのみ使用されます。これは通常、物理学および微分幾何学の微分方程式で使用されます。^{[ 25 ]}しかし、ドット記法は高次微分（4次以上）では扱いにくくなり、複数の独立変数を扱うことができません。 ${\displaystyle y}$ ${\displaystyle t}$ ${\displaystyle {\dot {y}}}$ ${\displaystyle {\ddot {y}}}$

もう 1 つの表記法はD 表記法で、これは微分演算子を記号⁠ ⁠${\displaystyle D}$ で表します。^{[ 19 ]} 1 次導関数は⁠ ⁠ と書き、高次の導関数は上付き文字で書きます。つまり、 - 次導関数は⁠ ⁠となります。この表記法はオイラー表記法と呼ばれることもありますが、レオンハルト・オイラーはこの表記法を使用しなかったようで、ルイ・フランソワ・アントワーヌ・アルボガストによって導入されました。^{[ 26 ]}偏微分を示すには、微分する変数を下付き文字で示します。たとえば、関数⁠ ⁠ の場合、 ⁠ ⁠に関する偏微分は⁠ ⁠と書きます。高次の偏微分は上付き文字または複数の下付き文字で示すことができ、たとえば⁠ ⁠および⁠ ⁠となります。^{[ 27 ]}${\displaystyle Df(x)}$ ${\displaystyle n}$ ${\displaystyle D^{n}f(x)}$ ${\displaystyle u=f(x,y)}$ ${\displaystyle x}$ ${\displaystyle D_{x}u}$ ${\displaystyle D_{x}f(x,y)}$ ${\textstyle D_{xy}f(x,y)={\frac {\partial }{\partial y}}{\Bigl (}{\frac {\partial }{\partial x}}f(x,y){\Bigr )}}$ ${\displaystyle \textstyle D_{x}^{2}f(x,y)={\frac {\partial }{\partial x}}{\Bigl (}{\frac {\partial }{\partial x}}f(x,y){\Bigr )}}$

計算規則

原則として、関数の微分は定義から差分商を考慮し、その極限を計算することで計算できます。いくつかの単純な関数の微分が分かれば、より複雑な関数の微分を単純な関数から求める規則を用いて、他の関数の微分をより簡単に計算できます。この微分を求めるプロセスは微分として知られています。^{[ 28 ]}

基本関数のルール

以下は、最も一般的な基本関数の微分に関する規則です。ここで、は実数、は自然対数の底で、約2.71828です。^{[ 29 ]}${\displaystyle a}$ ${\displaystyle e}$

• べき乗の導関数:

  ${\displaystyle {\frac {d}{dx}}x^{a}=ax^{a-1}}$

• 指数関数、自然対数関数、一般底対数関数:

  ${\displaystyle {\frac {d}{dx}}e^{x}=e^{x}}$

  ${\displaystyle {\frac {d}{dx}}a^{x}=a^{x}\ln(a)}$ 、のために${\displaystyle a>0}$

  ${\displaystyle {\frac {d}{dx}}\ln(x)={\frac {1}{x}}}$ 、のために${\displaystyle x>0}$

  ${\displaystyle {\frac {d}{dx}}\log _{a}(x)={\frac {1}{x\ln(a)}}}$ 、のために${\displaystyle x,a>0}$

• 三角関数：

  ${\displaystyle {\frac {d}{dx}}\sin(x)=\cos(x)}$

  ${\displaystyle {\frac {d}{dx}}\cos(x)=-\sin(x)}$

  ${\displaystyle {\frac {d}{dx}}\tan(x)=\sec ^{2}(x)={\frac {1}{\cos ^{2}(x)}}=1+\tan ^{2}(x)}$

• 逆三角関数：

  ${\displaystyle {\frac {d}{dx}}\arcsin(x)={\frac {1}{\sqrt {1-x^{2}}}}}$ 、のために${\displaystyle -1<x<1}$

  ${\displaystyle {\frac {d}{dx}}\arccos(x)=-{\frac {1}{\sqrt {1-x^{2}}}}}$ 、のために${\displaystyle -1<x<1}$

  ${\displaystyle {\frac {d}{dx}}\arctan(x)={\frac {1}{1+x^{2}}}}$

複合関数のルール

以下の規則により、基本関数の導関数から多くの関数の導関数を導くことができる。^{[ 30 ]}

• 定数ルール： が定数関数である場合、すべての⁠ ⁠に対して、 ${\displaystyle f}$ ${\displaystyle x}$

  ${\displaystyle f'(x)=0.}$

• 和則：

  ${\displaystyle (\alpha f+\beta g)'=\alpha f'+\beta g'}$ すべての関数およびすべての実数および⁠ ⁠に対して。${\displaystyle f}$ ${\displaystyle g}$ ${\displaystyle \alpha }$ ${\displaystyle \beta }$

• 製品ルール：

  ${\displaystyle (fg)'=f'g+fg'}$ すべての関数および⁠ ⁠について。特別なケースとして、この規則には、定数規則によりが定数である場合に、という事実が含まれます。${\displaystyle f}$ ${\displaystyle g}$ ${\displaystyle (\alpha f)'=\alpha f'}$ ${\displaystyle \alpha }$ ${\displaystyle \alpha 'f=0\cdot f=0}$

• 商の法則：

  ${\displaystyle \left({\frac {f}{g}}\right)'={\frac {f'g-fg'}{g^{2}}}}$ g ≠ 0である すべての関数およびすべての入力に対して。${\displaystyle f}$ ${\displaystyle g}$

• 合成関数の連鎖律： ⁠ ⁠${\displaystyle f(x)=h(g(x))}$ ならば、

  ${\displaystyle f'(x)=h'(g(x))\cdot g'(x).}$

計算例

で与えられる関数の微分はです。 ここで、 第2項は連鎖律、第3項は積の法則を用いて計算されました。基本関数の既知の微分、、、、、および、定数も使用されました ${\displaystyle f(x)=x^{4}+\sin \left(x^{2}\right)-\ln(x)e^{x}+7}$ $${\displaystyle {\begin{aligned}f'(x)&=4x^{(4-1)}+{\frac {d\left(x^{2}\right)}{dx}}\cos \left(x^{2}\right)-{\frac {d\left(\ln {x}\right)}{dx}}e^{x}-\ln(x){\frac {d\left(e^{x}\right)}{dx}}+0\\&=4x^{3}+2x\cos \left(x^{2}\right)-{\frac {1}{x}}e^{x}-\ln(x)e^{x}.\end{aligned}}}$$ ${\displaystyle x^{2}}$ ${\displaystyle x^{4}}$ ${\displaystyle \sin(x)}$ ${\displaystyle \ln(x)}$ ${\displaystyle \exp(x)=e^{x}}$ ${\displaystyle 7}$

反微分

関数の反微分とは、その導関数が である関数のことです。反微分は一意ではありません。が の反微分であれば、 も の反微分です。ここでは任意の定数です。定数の微分は0だからです。^{[ 31 ]}微積分学の基本定理は、関数の反微分を求めることで、その関数で囲まれた図形の面積を計算できることを示しています。より正確には、閉区間における関数の積分は、その区間の端点で評価された反微分の値の差に等しくなります。^{[ 32 ]}${\displaystyle f}$ ${\displaystyle f}$ ${\displaystyle A}$ ${\displaystyle f}$ ${\displaystyle A+c}$ ${\displaystyle c}$

高階微分

高階導関数は、関数を繰り返し微分した結果です。 が微分可能関数であるとすると、 の導関数は 1 階導関数で、⁠ ⁠と表記されます。 の導関数は2 階導関数で、⁠ ⁠と表記され、 の導関数は3 階導関数で、⁠ ⁠と表記されます。このプロセスを続けると、存在する場合、⁠ ⁠番目の導関数は⁠ ⁠番目の導関数の導関数、つまり⁠ ⁠階の導関数になります。上で説明したように、関数の導関数の一般化は⁠ ⁠と表記できます。^{[ 33 ]}連続する導関数 を持つ関数は回微分可能と呼ばれます。-階導関数が連続する場合、関数は⁠ ⁠微分可能クラスであると言われます。^{[ 34 ]}無限数の導関数を持つ関数は、無限微分可能または滑らかと呼ばれます。^{[ 35 ]}任意の多項式関数は無限に微分可能であり、繰り返し微分をとると最終的には定数関数となり、その関数のそれ以降の微分はすべてゼロになる。^{[ 36 ]}${\displaystyle f}$ ${\displaystyle f}$ ${\displaystyle f'}$ ${\displaystyle f'}$ ${\displaystyle f''}$ ${\displaystyle f''}$ ${\displaystyle f'''}$ ${\displaystyle n}$ ${\displaystyle (n-1)}$ ${\displaystyle n}$ ${\displaystyle f}$ ${\displaystyle f^{(n)}}$ ${\displaystyle k}$ ${\displaystyle k}$ ${\displaystyle k}$ ${\displaystyle C^{k}}$

高階微分の応用例の一つは物理学です。例えば、関数⁠ ⁠ が${\displaystyle x}$ 物体の時間に対する位置を表す場合、⁠ ⁠ は${\displaystyle x'}$ 物体の速度を表し、⁠ ⁠ は${\displaystyle x''}$ 物体の加速度を表します。^{[ 28 ]}そして⁠ ⁠ は${\displaystyle x'''}$ 物体のジャークを表します。^{[ 37 ]}

他の次元では

ベクトル値関数

実変数のベクトル値関数は、実数をあるベクトル空間 のベクトルに送信します。ベクトル値関数は、その座標関数 に分割することができ、つまり となります。これには、たとえば、または内のパラメトリック曲線が含まれます。座標関数は実数値関数であるため、上記の微分の定義が適用されます。 の微分は、座標が座標関数の微分である接線ベクトルと呼ばれるベクトルとして定義されます。つまり、 ^{[ 38 ]} 極限が存在する場合です。分子の減算は、スカラーではなくベクトルの減算です。 の微分が⁠ ⁠のすべての値に対して存在する場合、は別のベクトル値関数です。^{[ 38 ]}${\displaystyle \mathbf {y} }$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle y_{1}(t),y_{2}(t),\dots ,y_{n}(t)}$ ${\displaystyle \mathbf {y} =(y_{1}(t),y_{2}(t),\dots ,y_{n}(t))}$ ${\displaystyle \mathbb {R} ^{2}}$ ${\displaystyle \mathbb {R} ^{3}}$ ${\displaystyle \mathbf {y} (t)}$ $${\displaystyle \mathbf {y} '(t)=\lim _{h\to 0}{\frac {\mathbf {y} (t+h)-\mathbf {y} (t)}{h}},}$$ ${\displaystyle \mathbf {y} }$ ${\displaystyle t}$ ${\displaystyle \mathbf {y} '}$

偏微分

関数は複数の変数に依存することがあります。複数の変数を持つ関数の偏微分とは、他の変数を一定に保ったまま、そのうちの1つの変数について微分したものです。偏微分はベクトル解析と微分幾何学で用いられます。通常の微分と同様に、複数の表記法があります。関数の変数に関する偏微分は、次のように様々な表記法で表されます ${\displaystyle f(x,y,\dots )}$ ${\displaystyle x}$

${\displaystyle f_{x}}$ 、、、、 または、${\displaystyle f'_{x}}$ ${\displaystyle \partial _{x}f}$ ${\displaystyle {\frac {\partial }{\partial x}}f}$ ${\displaystyle {\frac {\partial f}{\partial x}}}$

他の可能性もある。^{[ 39 ]}これは、関数の -方向の変化率と考えることができる。^{[ 40 ]}ここで、∂は丸められたdであり、偏微分記号と呼ばれる。文字dと区別するために、∂ は「ディー」ではなく「ダー」、「デル」、または「パーシャル」と発音されることがある。^{[ 41 ]}例えば、⁠ ⁠とすると、関数の の両変数およびに関する偏微分はそれぞれ次のようになる。 一般に、点における方向 の関数の偏微分は次のように定義される。^{[ 42 ]}${\displaystyle x}$ ${\displaystyle f(x,y)=x^{2}+xy+y^{2}}$ ${\displaystyle f}$ ${\displaystyle x}$ ${\displaystyle y}$ $${\displaystyle {\frac {\partial f}{\partial x}}=2x+y,\qquad {\frac {\partial f}{\partial y}}=x+2y.}$$ ${\displaystyle f(x_{1},\dots ,x_{n})}$ ${\displaystyle x_{i}}$ ${\displaystyle (a_{1},\dots ,a_{n})}$ $${\displaystyle {\frac {\partial f}{\partial x_{i}}}(a_{1},\ldots ,a_{n})=\lim _{h\to 0}{\frac {f(a_{1},\ldots ,a_{i}+h,\ldots ,a_{n})-f(a_{1},\ldots ,a_{i},\ldots ,a_{n})}{h}}.}$$

これは、複数の実変数を持つ関数の研究において基本的なものです。 をそのような実数値関数とします。に関するすべての偏微分が点⁠ ⁠で定義されている場合、これらの偏微分はにおけるの勾配 と呼ばれるベクトルを定義します 。 が任意の領域内の任意の点で微分可能である場合、勾配は点をベクトル に写すベクトル値関数です。したがって、勾配はベクトル場を決定します。^{[ 43 ]}${\displaystyle f(x_{1},\dots ,x_{n})}$ ${\displaystyle f}$ ${\displaystyle x_{j}}$ ${\displaystyle (a_{1},\dots ,a_{n})}$ $${\displaystyle \nabla f(a_{1},\ldots ,a_{n})=\left({\frac {\partial f}{\partial x_{1}}}(a_{1},\ldots ,a_{n}),\ldots ,{\frac {\partial f}{\partial x_{n}}}(a_{1},\ldots ,a_{n})\right),}$$ ${\displaystyle f}$ ${\displaystyle a}$ ${\displaystyle f}$ ${\displaystyle \nabla f}$ ${\displaystyle (a_{1},\dots ,a_{n})}$ ${\displaystyle \nabla f(a_{1},\dots ,a_{n})}$

方向微分

が⁠ ⁠上の実数値関数である場合、 ⁠ の偏微分は座標軸の方向におけるその変化を測定します。例えば、 ⁠ が ⁠ ⁠と⁠ ⁠の関数である場合、その偏微分は ⁠ と⁠ ⁠方向における⁠ の変化を測定します。ただし、対角線⁠ ⁠に沿った方向など、他の方向における⁠ の変化を直接測定するものではありません。これらは方向微分を用いて測定されます。ベクトル⁠ ⁠が与えられた場合、点 ⁠における ⁠の方向微分は次のようになります。^{[ 44 ]}${\displaystyle f}$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle f}$ ${\displaystyle f}$ ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle f}$ ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle f}$ ${\displaystyle y=x}$ ${\displaystyle \mathbf {v} =(v_{1},\ldots ,v_{n})}$ ${\displaystyle f}$ ${\displaystyle \mathbf {v} }$ ${\displaystyle \mathbf {x} }$ $${\displaystyle D_{\mathbf {v} }{f}(\mathbf {x} )=\lim _{h\rightarrow 0}{\frac {f(\mathbf {x} +h\mathbf {v} )-f(\mathbf {x} )}{h}}.}$$

のすべての偏微分が存在し、⁠ ⁠で連続である場合、それらは次の式によって方向の の方向微分を決定します：^{[ 45 ]}${\displaystyle f}$ ${\displaystyle \mathbf {x} }$ ${\displaystyle f}$ ${\displaystyle \mathbf {v} }$ $${\displaystyle D_{\mathbf {v} }{f}(\mathbf {x} )=\sum _{j=1}^{n}v_{j}{\frac {\partial f}{\partial x_{j}}}.}$$

全微分とヤコビ行列

が の開部分集合から⁠ ⁠への関数である場合、の任意の方向への方向微分は、その点およびその方向における への最良の線形近似です。しかし、⁠ ⁠の場合には、単一の方向微分では の挙動の完全な描像を与えることはできません。全微分は、すべての方向を一度に考慮することにより完全な描像を与えます。つまり、⁠ ⁠から始まる任意のベクトルに対して、線形近似式が成り立ちます。^{[ 46 ]} 単変数微分と同様に、はこの近似での誤差が可能な限り小さくなるように選択されます。におけるの全微分は、次のようになる唯一の線形変換です。 ^{[ 46 ]} ここでは⁠ ⁠のベクトルであるため、分母のノルムは 上の標準の長さです。しかし、は⁠ ⁠のベクトルであり、分子のノルムは 上の標準の長さです。^{[ 46 ]}が⁠ ⁠から始まるベクトルである場合、 はによるのプッシュフォワードと呼ばれます。^{[ 47 ]}${\displaystyle f}$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle \mathbb {R} ^{m}}$ ${\displaystyle f}$ ${\displaystyle f}$ ${\displaystyle n>1}$ ${\displaystyle f}$ ${\displaystyle \mathbf {v} }$ ${\displaystyle \mathbf {a} }$ $${\displaystyle f(\mathbf {a} +\mathbf {v} )\approx f(\mathbf {a} )+f'(\mathbf {a} )\mathbf {v} .}$$ ${\displaystyle f'(\mathbf {a} )}$ ${\displaystyle f}$ ${\displaystyle \mathbf {a} }$ ${\displaystyle f'(\mathbf {a} )\colon \mathbb {R} ^{n}\to \mathbb {R} ^{m}}$ $${\displaystyle \lim _{\mathbf {h} \to 0}{\frac {\lVert f(\mathbf {a} +\mathbf {h} )-(f(\mathbf {a} )+f'(\mathbf {a} )\mathbf {h} )\rVert }{\lVert \mathbf {h} \rVert }}=0.}$$ ${\displaystyle \mathbf {h} }$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle f'(\mathbf {a} )\mathbf {h} }$ ${\displaystyle \mathbb {R} ^{m}}$ ${\displaystyle \mathbb {R} ^{m}}$ ${\displaystyle v}$ ${\displaystyle a}$ ${\displaystyle f'(\mathbf {a} )\mathbf {v} }$ ${\displaystyle \mathbf {v} }$ ${\displaystyle f}$

全微分が⁠ ⁠${\displaystyle \mathbf {a} }$ で存在する場合、 のすべての偏微分と方向微分は⁠ ⁠で存在し、すべての⁠ ⁠に対して、は ⁠ ⁠方向の⁠ ⁠方向微分です。 が座標関数を使用して書かれ、⁠ ⁠となる場合、全微分は偏微分を使用して行列として表すことができます。この行列は⁠ ⁠におけるヤコビ行列と呼ばれます。^{[ 48 ]}${\displaystyle f}$ ${\displaystyle \mathbf {a} }$ ${\displaystyle \mathbf {v} }$ ${\displaystyle f'(\mathbf {a} )\mathbf {v} }$ ${\displaystyle f}$ ${\displaystyle \mathbf {v} }$ ${\displaystyle f}$ ${\displaystyle f=(f_{1},f_{2},\dots ,f_{m})}$ ${\displaystyle f}$ ${\displaystyle \mathbf {a} }$ $${\displaystyle f'(\mathbf {a} )=\operatorname {Jac} _{\mathbf {a} }=\left({\frac {\partial f_{i}}{\partial x_{j}}}\right)_{ij}.}$$

一般化

微分の概念は、他の多くの状況に拡張できます。共通点は、ある点における関数の微分は、その点における関数の 線形近似として機能するということです

• 微分法の重要な一般化は、複素変数の複素関数、例えば複素数（の領域）から⁠ ⁠への関数に関係する。このような関数の微分法の概念は、定義において実変数を複素変数に置き換えることによって得られる。^{[ 49 ] を}複素数を⁠ ⁠と書いて⁠ ⁠と同一視すると、からへの微分可能な関数は、からへの関数として確かに微分可能である（その偏微分がすべて存在するという意味で）が、その逆は一般には成り立たない。複素微分法は、実微分が複素線型である場合にのみ存在し、これにより、コーシー・リーマン方程式と呼ばれる偏微分法の間に関係が課せられる（正則関数を参照）。^{[ 50 ]}${\displaystyle \mathbb {C} }$ ${\displaystyle \mathbb {C} }$ ${\displaystyle \mathbb {C} }$ ${\displaystyle \mathbb {R} ^{2}}$ ${\displaystyle z}$ ${\displaystyle x+iy}$ ${\displaystyle \mathbb {C} }$ ${\displaystyle \mathbb {C} }$ ${\displaystyle \mathbb {R} ^{2}}$ ${\displaystyle \mathbb {R} ^{2}}$
• もうひとつの一般化は、微分可能あるいは滑らかな多様体間の関数に関するものである。直感的に言えば、そのような多様体は、各点の近くをその接空間と呼ばれるベクトル空間で近似できる空間である。典型的な例は、 ⁠ ⁠内の滑らかな面である。 ⁠ ⁠内のある点における多様体間の（微分可能な）写像の微分（または微分）は、 ⁠ ⁠ における ⁠ ⁠の接空間から⁠ ⁠における⁠ ⁠の接空間への線型写像である。微分関数は、 ⁠ ⁠と⁠ ⁠の接束間の写像となる。この定義は微分幾何学で用いられる。^{[ 51 ]}${\displaystyle M}$ ${\displaystyle x}$ ${\displaystyle \mathbb {R} ^{3}}$ ${\displaystyle f:M\to N}$ ${\displaystyle x}$ ${\displaystyle M}$ ${\displaystyle M}$ ${\displaystyle x}$ ${\displaystyle N}$ ${\displaystyle f(x)}$ ${\displaystyle M}$ ${\displaystyle N}$
• 微分はバナッハ空間のようなベクトル空間間の写像に対しても定義することができ、その一般化はガトー微分とフレシェ微分である。^{[ 52 ]}
• 古典的な微分法の欠点の一つは、非常に多くの関数が微分不可能であるということです。しかしながら、微分の概念を拡張し、弱微分と呼ばれる概念を用いることで、すべての連続関数とその他多くの関数を微分可能にする方法があります。これは、連続関数を超関数空間と呼ばれるより広い空間に埋め込み、関数が「平均的に」微分可能であることのみを要求するという考え方です。^{[ 53 ]}
• 微分の性質は、代数学や位相幾何学における多くの類似の対象の導入と研究に影響を与えてきた。例えば、微分代数学が挙げられる。ここでは、環、イデアル、体など、抽象代数学におけるいくつかのトピックの導出が扱われる。^{[ 54 ]}
• 微分法の離散的等価物は差分である。微分積分学の研究は、時間スケール微分積分学における差分積分学と統合される。^{[ 55 ]}
• 算術微分は、素因数分解によって整数に対して定義される関数である。これは積の法則との類似性がある。^{[ 56 ]}

参照

• 共変微分
• 微分
• 外微分
• 関数微分
• リー微分

注釈

1. Apostol 1967 , p. 160; Stewart 2002 , pp. 129–130; Strang et al. 2023 , p.  224
2. Apostol 1967、p.160; Stewart 2002、p.127; Strang et al. 2023、  p.220。
3. Gonick 2012、p.83; Thomas et al. 2014、p.60。
4. Gonick 2012、p.88; Strang et al. 2023、  p.234。
5. Gonick 2012、p.83; Strang et al. 2023、  p.232。
6. ゴニック 2012、77～80頁。
7. トンプソン1998、34、104頁；スチュワート2002、128頁。
8. トンプソン 1998、84～85頁。
9. Keisler 2012、902–904 ページ。
10. Keisler 2012、p. 45;ヘンレ & クラインバーグ 2003、p. 66.
11. ゴニック 2012、p. 156;トーマスら。 2014 年、p. 114;ストラングら。 2023、p.  237 .
12. ゴニック 2012、p. 149;トーマスら。 2014 年、p. 113;ストラングら。 2023、p.  237 .
13. ゴニック 2012、p. 156;トーマスら。 2014 年、p. 114;ストラングら。 2023 、 237–238ページ 。
14. ヤシェク 1922 ;ヤルニク 1922 ;リシュリク 1923 年。
15. デビッド 2018 .
16. Banach 1931 、 Hewitt & Stromberg 1965で引用。
17. アポストル 1967、p. 172;カジョリ 2007、p. 204.
18. ムーア＆シーゲル 2013、110ページ。
19. Varberg、Purcell、Rigdon 2007、pp.125–126。
20. 微積分学の極限論的定式化において、様々な著者が記号 に様々な意味を割り当ててきました。Varberg , Purcell & Rigdon 2007、p. 119やStewart 2002 、p. 177などの著者は、には意味を割り当てず、記号 の一部としてのみ。また、 を独立変数 として定義し、によって。非標準解析では、 は無限小として定義されています。これは、関数⁠ ⁠の外微分としても解釈されます。詳細については、微分（無限小）を参照してください。${\displaystyle du}$ ${\displaystyle du}$ ${\textstyle {\frac {du}{dx}}}$ ${\displaystyle dx}$ ${\displaystyle du}$ ${\displaystyle \textstyle du=dxf'(x)}$ ${\displaystyle du}$ ${\displaystyle u}$
21. シュワルツマン1994、171頁； カジョリ1923、6～7頁、10～12頁、21～24頁。
22. ムーア＆シーゲル 2013、p.110;グッドマン 1963、pp.78-79。
23. ヴァールバーグ、パーセル、リグドン、2007 年、125–126 ページ。カジョリ 2007、p. 228.
24. Choudary & Niculescu 2014、p.  222 ;アポストル 1967 年、p. 171.
25. エヴァンス 1999、63ページ；クレイジグ 1991、1ページ。
26. カジョリ 1923 .
27. アポストル 1967、p. 172;ヴァールバーグ、パーセル、リグドン、2007 年、125 ～ 126 ページ。
28. アポストル 1967年、160ページ。
29. Varberg, Purcell & Rigdon 2007 . べき乗則については133ページ、三角関数については115～116ページ、自然対数については326ページ、底⁠ ⁠の指数関数については338～339ページ、底${\displaystyle e}$ ⁠ ⁠${\displaystyle a}$ の指数関数については343ページ、底⁠ ⁠${\displaystyle a}$ の対数関数については344ページ、三角関数の逆関数については369ページを参照してください。
30. 定数則と和則については、それぞれApostol 1967、161ページと164ページを参照。積則、商則、連鎖則については、それぞれVarberg, Purcell & Rigdon 2007、111–112ページと119ページを参照。積則の特殊なケース、すなわち定数と関数の積については、 Varberg, Purcell & Rigdon 2007、108–109ページを参照。
31. ストラングら。 2023 、 485–486ページ 。
32. ストラングら。 2023 、 552–559ページ 。
33. アポストル 1967、p. 160;ヴァールバーグ、パーセル、リグドン、2007 年、125 ～ 126 ページ。
34. ワーナー 1983、5ページ。
35. デブナス & シャー 2015、p. ４０．
36. カロザーズ2000、176ページ 。
37. スチュワート2002、193ページ。
38. スチュワート 2002、893ページ。
39. スチュワート2002、947ページ； クリストファー2013、682ページ。
40. スチュワート2002、949ページ 。
41. Silverman 1989、p.  216 ; Bhardwaj 2005、 p. 6.4を参照。
42. Mathai & Haubold 2017、p. ５２．
43. Gbur 2011、36～37頁。
44. ヴァールベリ、パーセル、リグドン、2007 年、p. 642.
45. グスマン2003、35ページ 。
46. ダヴヴァズ2023、266頁 。
47. Lee 2013、72ページ。
48. ダヴヴァズ2023、267頁 。
49. ルソス 2014、303ページ。
50. Gbur 2011、261–264頁。
51. グレイ、アッベナ、サラモン、2006 年、p.  826。
52. Azegami 2020 .ガトー導関数についてはp. 209 、フレシェ導関数についてはp. 211を参照。
53. フナロ 1992、84 ～85頁 。
54. コルチン1973、58、126頁 。​​
55. ゲオルギエフ2018、8ページ 。
56. バーボー 1961 .

参考文献

• アポストル、トム・M.（1967年6月）、微積分学 第1巻：線形代数入門付き1変数微積分学、第1巻（第2版）、Wiley、ISBN 978-0-471-00005-1
• 畔上秀之（2020）「形状最適化問題」、Springer Optimization and Its Applications、第164巻、Springer、doi：10.1007/978-981-15-7618-8、ISBN 978-981-15-7618-8, S2CID  226442409
• バナッハ、シュテファン(1931)、 「数学的カテゴリーの数学的機能について」、Studia Math.、3 (3): 174– 179、doi : 10.4064/sm-3-1-174-179
• Barbeau, EJ (1961). 「算術微分に関する考察」 . Canadian Mathematical Bulletin . 4 (2): 117– 122. doi : 10.4153/CMB-1961-013-0 . Zbl  0101.03702 .
• Bhardwaj, RS (2005)、『経済とビジネスのための数学』（第2版）、Excel Books India、ISBN 9788174464507
• カジョリ、フロリアン(1923)、「微積分記法の歴史」、Annals of Mathematics、25 (1): 1– 46、doi : 10.2307/1967725、hdl : 2027/mdp.39015017345896、JSTOR  1967725
• カジョリ、フロリアン（2007年）『数学記法の歴史』第2巻、コジモクラシックス、ISBN 978-1-60206-713-4
• Carothers, NL (2000)、『実分析』、ケンブリッジ大学出版局
• Choudary, ADR; Niculescu, Constantin P. (2014), Real Analysis on Intervals , Springer India, doi : 10.1007/978-81-322-2148-7 , ISBN 978-81-322-2148-7
• クリストファー、エセックス（2013年）『微積分：完全コース』ピアソン、682ページ、ISBN 9780321781079 OCLC  872345701
• リチャード・クーラント、ジョン・フリッツ（1998年12月22日）『微積分と解析入門』第1巻、シュプリンガー・フェアラーク、doi : 10.1007/978-1-4613-8955-2、ISBN 978-3-540-65058-4
• デイヴィッド、クレア（2018）「動的システムのバイパス：ワイエルシュトラス関数のグラフのボックスカウント次元を取得する簡単な方法」国際幾何学センター紀要、11（2）、ウクライナ科学アカデミー：53–68、arXiv：1711.10349、doi：10.15673/tmgc.v11i2.1028
• Davvaz, Bijan (2023), Vectors and Functions of Multiple Variables , Springer, doi : 10.1007/978-981-99-2935-1 , ISBN 978-981-99-2935-1、S2CID  259885793
• デブナス、ロケナス；シャー、フィルドゥス・アフマド（2015年）、ウェーブレット変換とその応用（第2版）、ビルクハウザー、doi：10.1007/978-0-8176-8418-1、ISBN 978-0-8176-8418-1
• エヴァンス、ローレンス（1999年）『偏微分方程式』アメリカ数学会、ISBN 0-8218-0772-2
• イーブス、ハワード（1990年1月2日）『数学史入門』（第6版）、ブルックス・コール、ISBN 978-0-03-029558-4
• フナロ、ダニエレ（1992）「微分方程式の多項式近似」、物理学モノグラフ講義ノート、第8巻、シュプリンガー、doi：10.1007/978-3-540-46783-0、ISBN 978-3-540-46783-0
• グバー、グレッグ（2011年）『光物理学と工学のための数学的手法』、ケンブリッジ大学出版局、Bibcode：2011mmop.book.....G、ISBN 978-1-139-49269-0
• ゲオルギエフ、スヴェトリン・G. (2018)、『分数動的計算と時間スケール上の分数動的方程式』、シュプリンガー、doi : 10.1007/978-3-319-73954-0、ISBN 978-3-319-73954-0
• グッドマン、AW（1963年）『解析幾何学と微積分』マクミラン社
• ゴニック、ラリー（2012年）、微積分への漫画ガイド、ウィリアム・モロー、ISBN 978-0-06-168909-3
• アルフレッド・グレイ、エルサ・アッベナ、サイモン・サラモン（2006年）『Mathematicaによる曲線と曲面の現代微分幾何学』 CRC Press、ISBN 978-1-58488-448-4
• グスマン、アルベルト（2003）『多変数関数の微分と積分』、シュプリンガー、doi：10.1007/978-1-4612-0035-2、ISBN 978-1-4612-0035-2
• ヘンレ、ジェームズ・M.；クラインバーグ、ユージン・M.（2003年）『微分積分学』ドーバー出版、ISBN 978-0-486-42886-4
• ヒューイット、エドウィン；ストロンバーグ、カール・R.（1965）、実解析と抽象解析、シュプリンガー・フェアラーク、定理17.8、doi：10.1007 / 978-3-662-29794-0、ISBN 978-3-662-28275-5
• ヤシェク、マーティン（1922）、「Funkce Bolzanova」（PDF）、Časopis pro Pěstování Matematiky a Fyziky（チェコ語）、51（2）：69– 76、doi：10.21136/CPMF.1922.121916
• Jarník, Vojtěch (1922)、「O funkci Bolzanově」(PDF)、Časopis pro Pěstování Matematiky a Fyziky (チェコ語)、51 (4): 248–264、doi : 10.21136/CPMF.1922.109021英語版はこちらをご覧ください。
• Keisler, H. Jerome (2012) [1986],初等微積分学：無限小数を用いたアプローチ（第2版）、Prindle, Weber & Schmidt、ISBN 978-0-871-50911-6
• コルチン、エリス (1973)、『微分代数と代数群』、アカデミック・プレス、ISBN 978-0-08-087369-5
• クレイジグ、エルウィン（1991年）『微分幾何学』ニューヨーク：ドーバー、ISBN 0-486-66721-9
• ラーソン、ロン、ホステラー、ロバート・P、エドワーズ、ブルース・H（2006年2月28日）『微積分：超越関数入門』（第4版）、ホートン・ミフリン社、ISBN 978-0-618-60624-5
• リー、ジョン・M. (2013)、『滑らかな多様体入門』、Graduate Texts in Mathematics、第218巻、Springer、doi : 10.1007/978-0-387-21752-9、ISBN 978-0-387-21752-9
• Mathai, AM; Haubold, HJ (2017), Fractional and Multivariable Calculus: Model Building and Optimization Problems , Springer, doi : 10.1007/978-3-319-59993-9 , ISBN 978-3-319-59993-9
• ムーア、ウィル・H.、シーゲル、デイビッド・A.（2013年）『政治社会研究のための数学講座』プリンストン大学出版局、ISBN 978-0-691-15995-9
• ルソス、イオアニス・M. (2014)、『不完全リーマン積分』、CRCプレス、ISBN 978-1-4665-8807-3
• Rychlík, Karel (1923), Über eine Funktion aus Bolzanos handschriftlichem Nachlasse
• シュワルツマン、スティーブン（1994）『数学の言葉：英語で使われる数学用語の語源辞典』アメリカ数学協会、ISBN 9781614445012
• シルバーマン、リチャード・A.（1989年）『微積分学入門：応用編』クーリエ社、ISBN 9780486660974
• スチュワート、ジェームズ（2002年12月24日）、微積分（第5版）、ブルックス・コール、ISBN 978-0-534-39339-7
• ストラング、ギルバート他 (2023)、『微積分学』第1巻、OpenStax、ISBN 978-1-947172-13-5
• トーマス、ジョージ・B・ジュニア、ウィアー、モーリス・D、ハス、ジョエル（2014年）。トーマスの微積分（PDF）（第13版）。ピアソン社。ISBN 978-0-321-87896-02024年9月9日閲覧
• トンプソン、シルバヌス・P.（1998年9月8日）、『Calculus Made Easy』（改訂・更新・拡張版）、ニューヨーク：セント・マーチンズ・プレス、ISBN 978-0-312-18548-0
• ヴァーバーグ、デール・E.、パーセル、エドウィン・J.、リグドン、スティーブン・E. (2007) 『微積分学』（第9版）、ピアソン・プレンティス・ホール、ISBN 978-0131469686
• ワーナー、フランク・W. (1983)、『微分可能多様体とリー群の基礎』、シュプリンガー、ISBN 978-0-387-90894-6

外部リンク

• 「微分」、数学百科事典、EMSプレス、2001 [1994]
• カーンアカデミー：「ニュートン、ライプニッツ、そしてウサイン・ボルト」
• ワイスタイン、エリック W. 「微分」。MathWorld 。
• Wolfram Alphaのオンライン微分計算機。