重なり合う円のグリッド
| 正方形の円形グリッド | |||||
|---|---|---|---|---|---|
| 1歳以上 |  |  |  |  | 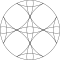 |
| 4 |  |  | 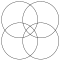 |  |  |
| 9 | 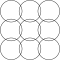 | 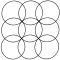 |  |  |  |
| 中心正方格子形状 | |||||
| 5 |  |  |  |  |  |
| 13 |  |  | 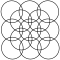 |  |  |
 |  |  |  |  | |
| 三角形の円グリッド | |||||
| 1歳以上 | 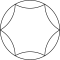 |  |  |  |  |
| 3 |  |  | 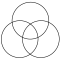 |  |  |
| 4 |  | 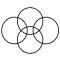 |  |  |  |
| 7 | 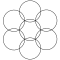 |  |  |  |  |
| 19 |  |  |  |  |  |
 |  |  |  |  | |
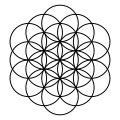
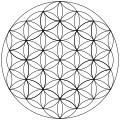
重なり合う円のグリッドは、二次元空間において等半径の円が重なり合うように繰り返される幾何学模様です。一般的に、デザインは三角形を中心とする円(単純な二つの円からなる「vesica piscis 」と呼ばれる形状)や、点が並ぶ 正方格子模様に基づいています。
7つの円が重なり合う模様は、紀元前7世紀以降の歴史的遺物に現れ、ローマ帝国時代には装飾として頻繁に用いられ、イスラム美術(ギリフ装飾)とゴシック美術の両方において中世の芸術的伝統に受け継がれました。ニューエイジ系の出版物 では、この重なり合う円の模様は「フラワー・オブ・ライフ」と呼ばれています。
特に興味深いのは、7 つの重なり合う円のパターンから派生した六角形または 6 枚の花びらのロゼットです。これは、17 世紀と 18 世紀のアルプスの民芸品で頻繁に使用されたことから「アルプスの太陽」としても知られています。
重なり合う円の三角形のグリッド

円の半径が円の間隔に等しい三角形の格子形状は、7つの重なり合う円の格子と呼ばれます。[ 1 ]この格子には、1点で交差する6つの円と、その交点を中心とする7番目の円が含まれます。
重なり合う円と類似した幾何学的構造は、古代から様々な装飾芸術において散発的に用いられてきました。この模様は、大衆文化、ファッション、宝飾品、タトゥー、装飾品など、幅広い分野で用いられています。
文化的意義
近東
重なり合う円の模様の最も古い例は紀元前7世紀または6世紀のもので、アッシリア王アッシュール・バーニ・アプリのドゥル・シャルキン宮殿(現在はルーブル美術館)の敷居で発見されました。[ 2 ]
このデザインは西暦紀元初期の数世紀に広く普及しました。初期の例としては、エジプトのアビドスにあるオシリス神殿の花崗岩の柱に描かれた、19個の重なり合う円の模様が5つあります。 [ 3 ]また、神殿の反対側の柱にも5つの模様があります。これらは赤い黄土色で描かれており、中には非常に薄くて判別が難しいものもあります。[ 4 ]これらの模様は落書きであり、エジプト固有の装飾品には見られません。そのほとんどは紀元後数世紀の初期のものとされていますが、 [ 5 ]中世や現代(20世紀初頭)に起源を持つ可能性も確実に否定できません。なぜなら、マーガレット・マレーが1904年にまとめた神殿の落書きの詳細なリストにこれらの絵は記載されていないからです。[ 6 ]
同様の模様は、魔女が建物に入らないようにするための厄除けの印としてイギリスで時々使われていました。[ 7 ]教会の奉献式で聖水が注がれた場所を示す奉献の十字架も重なり合った円の形をしています。
イスラム美術において、この模様は、イスラム幾何学模様の格子を構成するために用いられる円の配置法の一つである(他には四重または五重の模様として用いられる)。六芒星や十二芒星、そしてギリフと呼ばれる六角形の模様をデザインする際に用いられる。しかし、結果として得られる模様は、格子を構成する要素を隠蔽し、代わりに絡み合ったストラップワークのデザインを呈する。[ 8 ]
ヨーロッパ
7つの重なり合う円の模様は、ローマ時代のモザイク、例えば紀元前1世紀のヘロデ宮殿で見つかっています。 [ 9 ]この模様は、ローマ後期のカイザーアウグストの宝物(1961年発見)の銀板の1つに見られます。 [ 10 ]その後、ゴシック建築の装飾として、そしてさらに後期には近世ヨーロッパの民芸品にも見られます。中世後期の例として、ウェストミンスター寺院のコスマティ舗装(13世紀)が挙げられます。[ 11 ]レオナルド・ダ・ヴィンチはこの模様の数学的比率について明確に論じています。[ 12 ]
現代の用法
.jpg/440px-Flower_of_Life_pendant_(2).jpg)
「フラワー・オブ・ライフ」という名称は現代的で、ニューエイジ運動と関連付けられており、特にドランヴァロ・メルキゼデクの著書『フラワー・オブ・ライフの古代の秘密』(1999年)に由来するとされています。[ 13 ] [ 14 ]
この模様と現代名は、大衆文化、ファッション、ジュエリー、タトゥー、装飾品など、幅広い範囲で用いられるようになった。キルティングの模様は、正方形の模様と対比させて、ダイヤモンドの結婚指輪や三角形の結婚指輪と呼ばれてきた。ファッションで時折使用されるほか、[ 15 ]装飾芸術でも用いられる。例えば、ブリング・ミー・ザ・ホライズンのアルバム『Sempiternal』(2013年)では、61個の重なり合う円のグリッドがアルバムカバーの主要な特徴として用いられており、 [ 16 ]コールドプレイのアルバム『A Head Full of Dreams』(2015年)では、19個の重なり合う円のグリッドがアルバムカバーの中央部分として用いられている。 2015年10月最終週には、ロンドン地下鉄で『 A Head Full of Dreams』のカバーアートを描いたティーザーポスターが広く掲示された。[ 17 ]
アルプスの太陽(イタリア語:ソーレ・デッレ・アルピ)のシンボルは、1990年代から北イタリアのパダニア民族主義の象徴として使われてきました。 [ 18 ]この模様は、その地域の建物によく見られる模様に似ています。[ 19 ]
7 つの円からなる生命の花は、宇宙国家 アスガルディアの紋章にも使用されています。
ギャラリー
1、7、19個の円の六角形のバリエーション
以下の例では、パターンは六角形の輪郭を持ち、さらに外接しています。
- レオナルド・ダ・ヴィンチの『アトランティコス手稿』に描かれた絵(1478年から1519年)
- レオナルド・ダ・ヴィンチの絵(アトランティコ手稿、 307ページ)
- 完成した円弧を持つ1つの円
- 紀元前1世紀のヘロデ宮殿の浴場の7つの円のモザイクの床
- 完成した円弧と大きな円で囲まれた 19 個の円のシンボル
- エジプトのアビドスにあるオシリス神殿に赤い黄土で描かれた19個の円からなる2つのシンボル
- クレタ島、プレヴェリ修道院(モニ・プレヴェリ)の教会の南後陣にある19個の円形窓
- トルコ、エフェソスの19個の円模様
類似のパターン
以下の例では、パターンに六角形のアウトラインがありません。
- ルーブル美術館に展示されている、イラク北部のアッシュールバニパル王の宮殿の床装飾。紀元前645年のもの。
- コーヒーカップ(ドイツ、2022年)
工事
幾何学美術の教本を執筆したマーサ・バートフェルドは、1968年にこのデザインを独自に発見した経緯を説明しています。彼女の最初の定義は、「このデザインは半径1インチ(25mm)の円で構成され、各交点が新たな中心として機能します。このデザインは、奇数番目の点を区切る回数に応じて 無限に拡張できます」というものでした。
この図形は、ペンとコンパスを使って、前の円の中心に接する同じ直径の円を複数回連結することで描くことができます。2つ目の円は最初の円の任意の点を中心とします。その後に描く円はすべて、他の2つの円の交点を中心とします。
進行
このパターンは、次の表に示すように、同心円状の六角形の円環を外側に拡張することができます。最初の行は円環を示しています。2番目の行は、等角投影図で積み重ねられた球体の立方体を示しています。3番目の行は、一連の完全な円の中に部分的な円弧を配置して完成したパターンを示しています。
拡大集合には、1、7、19、37、61、91、127個の円と、さらに大きな六角形の円環が連続して存在します。円の数は 個で、nは環の数であり、中心六角数を形成します。
これらの重なり合う円は、 n単位の立方体の球を3次元空間に投影したものと見なすこともできます。球の中には2次元的に重なり合うものもあるため、円よりも球の数が多くなります。
| 1円 | 7円(8 − 1) | 19円(27 − 8) | 37円(64 − 27) | 61円(125 − 64) | 91円(216 − 125) | 127円(343 − 216) |
|---|---|---|---|---|---|---|
 |  |  |  |  |  |  |
| 1球(1×1×1) | 8球(2×2×2) | 27球(3×3×3) | 64球(4×4×4) | 125球(5×5×5) | 216球(6×6×6) | 343球(7×7×7) |
 |  |  |  |  |  |  |
| +12アーク | +24アーク | +36アーク | +48アーク | +60アーク | +72アーク | +84アーク |
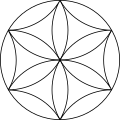 |  |  |  |  |  |  |
その他のバリエーション
もう一つの三角形格子は、円の間隔が半径の3倍の平方根となる形状が一般的です。リチャード・カーシュナーは1939年、この六角形格子の配置ほど効率的に平面を覆う円の配置は存在しないことを示しました。[ 20 ]
この円形パターンのオフセットコピーを 2 つ作成すると菱形のタイリングパターンが作成され、3 つのコピーを作成すると元の三角形のパターンが作成されます。
- 19個の円の例、最小被覆円パターン
- パターン(左)の2つのオフセットコピーは菱形のタイルパターンを作成します
- パターンのオフセットコピー3つ(左端の画像)で7つの円のパターンが完成します。
関連概念
二つの円からなる図形の中心レンズは、数学者ユークリッドにちなんで「魚の胞(vesica piscis)」と呼ばれます。二つの円は、トーラスの平面交差としてヴィラルソーの円とも呼ばれます。一方の円の内側でもう一方の円の外側にある領域は「月(lune)」と呼ばれます。
3つの円からなる図形はボロミオ環に似ており、ベン図の3つの集合の変種にも用いられます。交点の軌跡はトリケトラと呼ばれる一筆書きの軌跡を形成します。3つの円からなる図形の中心はルーローの三角形と呼ばれます。
 ヴェシカ・ピシス ヴェシカ・ピシス |  ボロミアンリング ボロミアンリング |  ベン図 ベン図 |  トリケトラ トリケトラ | 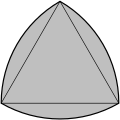 ルーローの三角形 ルーローの三角形 |
大円に沿った辺を持つ球面多面体の中には、重なり合う円として平面上に立体投影できるものもあります。
 八面体 八面体 |  立方八面体 立方八面体 |  二十面体 二十面体 |
七つの円の模様はイスラム美術で使用されていることからイスラムの七つの円の模様とも呼ばれています。
重なり合う円の正方形のグリッド
| ||
|
正方格子は、円が水平方向と垂直方向に並び、対角線上で交差する形で表現されます。対角線上で回転させると、模様が若干変化します。これは、2つの正方格子が互いの格子の隙間を中心として配置されているように見えるため、 「中心正方格子」とも呼ばれます。
これはインドネシアのバティックではカウンモチーフと呼ばれ、ジャワ島にある8世紀のヒンドゥー教寺院プランバナンの壁に描かれています。
これは古代メソポタミアの数学ではアプサミックムと呼ばれています。[ 21 ]
- 正方格子は面心立方格子で見られ、各球の周りには12個の球が接している。
- 関連する5つの重なり合う円のグリッドは、半分オフセットされた2組の重なり合う円から構成される[ 22 ]
参照
- 結び目理論
- 均一タイリング対称性変異 – 3D空間におけるパターン変異
参考文献
- ^イスラム美術と幾何学デザイン:学習活動
- ^ルーヴル美術館-Nr. AO 19915。ジョルジュ・ペロー、シャルル・チピエス、カルデアとアッシリアの美術史、vol. 1、ロンドン 1884、S. 240、 (gutenberg.org)
- ^ Weisstein, Eric W. 「生命の花」。MathWorld 。
- ^スチュワート、マルコム (2008). 「『フラワー・オブ・ライフ』とオシリオン ― 事実は空想よりも興味深い」エジプト旅行 (デヴィッド・ファーロング) . 2015年11月8日閲覧。
- ^ファーロング、デイヴィッド. 「オシリオンと生命の花」 . 2015年11月8日閲覧。ファーロングは、これらの彫刻の年代は紀元前535年以降、おそらく紀元後2世紀から4世紀にかけてであると述べている。彼の研究は、まだ完全に解読されていない隣接するギリシャ語のテキストに基づいている。テキストとデザインは、高さ4メートル(13フィート)を超える柱の頂上付近に配置されている。ファーロングは、円が描かれる前は神殿が砂で半分埋められていたため、円はプトレマイオス朝末期以降に作られた可能性が高いと示唆している。
- ^マレー、マーガレット・アリス (1904). 『アビドスのオシレイオン、ロンドン』 p. 35. 2015年11月4日閲覧。
- ^ケネディ、メイヴ(2016年10月31日)「魔女の痕跡:建物に残る古代の傷跡を探すよう市民に呼びかけ」ガーディアン紙。 2016年10月31日閲覧。
- ^ Broug, Eric (2008). Islamic Geometric Patterns . Thames and Hudson . pp. 22–23 and passim . ISBN 978-0-500-28721-7。
- ^ Katz, Eugene A.; Jin, Bih-Yaw (2016年8月). Huylebrouck, Dirk (編). 「フラーレン、多面体、そして中国の守護獅子」. 数学の観光者.数学インテリジェンサー. 38 (3): 61– 68. doi : 10.1007/s00283-016-9663-0 .
- ^ハンス・ウルリッヒ・インスティンスキー: Der spätrömische Silberschatzfund von Kaiseraugst.マインツ 1971、プラーク 85。
- ^ウェストミンスター寺院のコスマティ舗装。 2013年9月14日閲覧。
- ^アトランティカス写本、307r–309v、459rページ(1478年から1519年の間に作成されたもの)。
- ^バートフェルド、マーサ(2005年)『神聖幾何学マンダラの作り方』サンタフェ、ニューメキシコ州:Mandalart Creations、35ページ。ISBN 9780966228526. OCLC 70293628 .
- ^ワイスタイン、エリック・W.(2002年12月12日)CRCコンサイス数学百科事典第2版CRCプレス(2002年出版)p.1079. ISBN 1420035223。
- ^ Eg Zaman, Sana (2013年5月14日). 「Zaeem Jamalがドバイマリーナのプライベートヨットで新コレクションを発表」 . Haute Living . 2015年11月9日閲覧。
- ^ Cooper, Ed (2013年2月25日). 「ブリング・ミー・ザ・ホライズン:このアルバムは永遠に残るものになるべきだ」 . The Independent . 2015年10月23日時点のオリジナルよりアーカイブ。 2015年11月8日閲覧。
- ^ Denham, Jess (2015年11月6日). 「Coldplayのニューアルバム:ビヨンセとノエル・ギャラガーが『A Head Full of Dreams』に出演」 . The Independent . 2022年5月24日時点のオリジナルよりアーカイブ。 2015年11月8日閲覧。
- ^ 「Ilsignificato del simbolo del Sole delle Alpi」(イタリア語)。レガノルド。2014 年 1 月 12 日のオリジナルからアーカイブ。2014 年12 月 1 日に取得。
- ^イヴァーノ・ドルボロ (2010 年 6 月 6 日)。「S.エジディオ教会とアルプスの太陽のシンボル」。ストーリア ディ コンフィネ – ヴァッリ ディ ナティゾーネ。2015 年11 月 9 日に取得。
- ^球面パッキング、格子、群、ジョン・コンウェイ、ニール・JA・スローン共著、第2章、1.1節「重なり合う円による空間の被覆」、pp. 31–32。図2.1 平面を円で被覆する (b) 六方格子におけるより効率的または薄い被覆。 [1]
- ^メソポタミアの数学 2100–1600 BCE: 官僚制と教育における技術的定数(オックスフォード版楔形文字テキスト)、エレノア・ロブソン、クラレンドン・プレス、1999年、 ISBN 978-0198152460[2] books.google.com
- ^ 「円から正方形のグリッドを作成する」 。 2016年3月4日時点のオリジナルよりアーカイブ。2015年12月22日閲覧。
外部リンク
- ワイスタイン、エリック W. 「円-円交差」。MathWorld 。
- フラワー・オブ・ライフの秘密:意味、歴史、そしてミスティカでの描き方












.jpg/440px-Coffee_cup_with_overlapping_circles_grid_ornament_(Germany,_2022).jpg)













![関連する5つの重なり合う円のグリッドは、半分オフセットされた2組の重なり合う円から構成される[22]](http://upload.wikimedia.org/wikipedia/commons/thumb/e/ea/Square_five_overlapping_circle_grid.svg/120px-Square_five_overlapping_circle_grid.svg.png)

