定規とコンパスを使った作図

定規とコンパスを使って正六角形を作成する

幾何学において、定規とコンパスによる作図（定規とコンパスによる作図、ユークリッド作図、古典作図とも呼ばれる）は、理想的な定規とコンパスのみを使用して長さ、角度、およびその他の幾何学的図形を作図することです。

理想的な定規は定規と呼ばれ、長さは無限大で、辺は 1 つしかなく、目盛りは付いていないものと想定されます。コンパスには最大半径も最小半径もなく、紙から持ち上げると「折りたたまれる」ものと想定されるため、距離の変換に直接使用することはできません。(これは重要でない制約です。複数段階の手順を使用すれば、折りたためるコンパスでも距離を変換できます。コンパス同値定理を参照してください。ただし、折りたためないコンパスを定規に当てることは、定規に目盛りを付けるのと同じように見えるかもしれませんが、それでもニューシス構成は許されず、これが「目盛りなし」の真の意味です。以下の「目盛り付き定規」を参照してください。) より正式には、許される構成はユークリッドの『原論』の最初の 3 つの公理で認められるものだけです。

定規とコンパスを使用して作図できるすべての点は、コンパスのみを使用して作図することも、単一の円とその中心が与えられている場合は定規のみを使用して作図することもできることがわかります。

古代ギリシャの数学者は、定規とコンパスによる作図を初めて考案し、平面幾何学における古代の問題の多くがこの制約を課しています。古代ギリシャ人は多くの作図法を開発しましたが、場合によっては作図できませんでした。ガウスは、一部の多角形は作図可能ですが、ほとんどは作図できないことを示しまし た。最も有名な定規とコンパスの問題のいくつかは、1837 年にピエール・ヴァンツェルによって場の理論を用いて不可能であると証明されました。具体的には、任意の角度を三等分することと立方体の体積を 2 倍にすることです( § 不可能作図を参照)。これらの問題の多くは、他の幾何学的変換が許される限り簡単に解くことができます。たとえば、最初の 2 つの問題は、 ニューシス作図を使用して解くことができます。

代数学の観点から言えば、長さが構成可能であるのは、それが構成可能な数を表す場合のみであり、角度が構成可能であるのは、その余弦が構成可能な数である場合のみである。数が構成可能であるのは、四則演算と平方根の抽出を用いて表すことができ、高階根は表せない場合のみである。

定規とコンパスツール

定規とコンパス

コンパス

定規とコンパスの構図における「定規」と「コンパス」は、現実世界の定規とコンパスの理想化されたバージョンです。

• 定規は、目盛りのない無限に長い辺です。2点間に線分を引いたり、既存の線分を延長したりするためにのみ使用できます。
• このコンパスは、目盛りが付いていない状態でも、任意の大きさの半径を持つことができます（現実世界の一部のコンパスとは異なります）。円と円弧は、中心と円上の点という2点を基準に描くことができます。コンパスは折りたたむことも、折りたたまないこともできます（つまり、ページから取り出すと折りたたまれ、「保存された」半径は消去されます）。
• 構築された線と円は、精度が無限で幅がゼロです。

実際のコンパスは折り畳み式ではなく、現代の幾何学的構成ではこの特徴がしばしば利用されています。「折り畳み式コンパス」は、それほど強力ではないように思われるかもしれません。しかし、ユークリッドの『原論』第一巻の命題2にあるコンパス同値定理によれば、折り畳み式コンパスを使用しても力は失われません。この命題は真ですが、その証明には長く波瀾万丈な歴史があります。^{[ 1 ]}いずれにせよ、この同値性こそが、理想的なコンパスの定義においてこの特徴が規定されていない理由です。

それぞれの作図は数学的に正確でなければなりません。目測による距離の推定（作図を見てその正確さを推測すること）や定規の目盛りの使用は認められません。また、それぞれの作図は で終了しなければなりません。つまり、有限個のステップを持ち、近似値の限界であってはなりません。（無制限のステップ数が認められると、本来は不可能な作図が、極限に収束する無限の列によって可能になります。）

このように述べると、定規とコンパスによる作図は、深刻な実際的な問題というよりは社交ゲームのように見えますが、この制限の目的は、作図が正確に正しいことを証明できるようにすることです。

歴史

古代ギリシャの数学者は、最初に定規とコンパスを使った作図を試み、与えられた長さの和、差、積、比、平方根を作る方法を発見した。^{[ 2 ] : p. 1} また、与えられた角度の半分、面積が別の正方形の 2 倍である正方形、与えられた多角形と同じ面積を持つ正方形、3 辺、4 辺、5 辺の正多角形^{[ 2 ] : p. xi} （または与えられた多角形の辺の数の 2 倍の多角形^{[ 2 ] : pp. 49–50} ）を作ることもできた。 しかし、特別な場合を除いて、与えられた角度の 3 分の 1 を作ることも、与えられた円と同じ面積を持つ正方形を作ることも、他の辺の数を持つ正多角形を作ることもできなかった。^{[ 2 ] : p. xi} また、与えられた辺を持つ立方体の体積の 2 倍の体積を 持つ立方体の辺を作ることもできなかった。^{[ 2 ] : p. 29}

ヒポクラテスとメナイクモスは、双曲線と放物線の交点を見つけることで立方体の体積を 2 倍にできることを示したが、これらは定規とコンパスで作成することはできない。^{[ 2 ] : p. 30} 紀元前 5 世紀に、ヒッピアスは、一般角を三等分するとともに円を二等分するために、彼が方形曲線と呼んだ曲線を使用し、また、紀元前 2 世紀にニコメデスは、貝殻形を使用して任意の角度を三等分する方法を示した。^{[ 2 ] : p. 37} しかし、これらの方法も定規とコンパスだけでは実行できない。

未解決の問題は2千年の間進展がなかったが、1796年にガウスが17辺の正多角形が作図可能であることを示しました。5年後、ガウスはn辺の正多角形が作図可能であるための十分な基準を示しました。^{[ 2 ]：pp. 51 ff.}

1837年、ピエール・ヴァンツェルは、長さの立方根を構成することが不可能であることに基づき、任意の角を三等分することや立方体の体積を倍にすることが不可能であることの証明を発表しました^{[ 3 ]}。また、彼はガウスの十分構成可能性条件が正多角形にも必要であることを示しました^{[ 4 ] 。}

そして1882年にリンデマンは が超越数であることを示し、定規とコンパスを使って与えられた円と同じ面積の正方形を描くことは不可能であることを証明した。^{[ 2 ]：p.47} ${\displaystyle \pi }$

基本的な構造

基本的な構造

定規とコンパスを使った作図はすべて、既に作図済みの点、直線、円を使った5つの基本的な作図法を繰り返し適用することで構成されます。これらの作図法は以下のとおりです。

• 2点を通る線を作成する
• 1つの点を含み、別の点を中心とする円を作成する
• 2本の（平行でない）直線の交点を作成する
• 直線と円の交点に1 点または2 点を作成する(交差する場合)
• 2 つの円の交点に 1 点または 2 点を作成します (交差する場合)。

例えば、異なる2点から始めて、直線または2つの円を描くことができます（それぞれの点を中心とし、もう一方の点を通るように）。両方の円を描くと、交点に2つの新しい点が作成されます。元の2点とこれらの新しい点のいずれかを結ぶ線を引くと、正三角形が完成します。

したがって、あらゆる幾何学の問題には、記号（点と直線）の初期集合、アルゴリズム、そしていくつかの結果が存在します。この観点から見ると、幾何学は公理的代数と等価であり、その要素は記号に置き換えられます。おそらくガウスが最初にこれに気づき、いくつかの構成の不可能性を証明するために用いました。ヒルベルトが幾何学の公理の完全な集合を発見したのは、ずっと後のことでした。

一般的な定規とコンパスを使った作図

最もよく使用される定規とコンパスの構成は次のとおりです。

• 線分から垂直二等分線を作成する
• セグメントの中点を見つけます。
• 点から線に垂直な線を引きます。
• 角度を二等分する
• 線上の点を鏡像化する
• 円に接する点を通る直線の作成
• 同一直線上にない3点を通る円を描く
• 指定された点を通り、指定された直線と平行な線を描きます。

構築可能なポイント

代数演算に対応する定規とコンパスによる作図
x  =  a · b   (切片定理)	x  =  a / b   （切片定理）	x = √ a   （幾何平均定理）

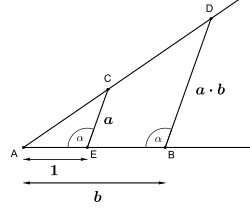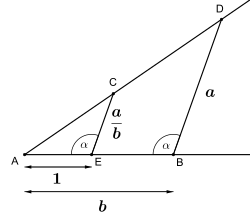二本の直線からなる直交座標系を用いて、幾何学に代数を関連付け、平面上の点をベクトルで表すことができます。そして、これらのベクトルを複素数として表すことができます。

直線と円の方程式を用いると、それらの交点は、直線上の2点、円の中心、円の半径を含む最小の体Fの二次拡大内にあることが示せます。つまり、交点は の形をとり、x、y、kはFに含まれます。 ${\displaystyle x+y={\sqrt {k}}}$

構成可能点体は平方根に関して閉じているので、有理係数の複素数体の有限な二次拡大列によって得られる点がすべて含まれる。上の段落により、任意の構成可能点はそのような拡大列によって得られる。この系として、構成可能点（したがって任意の構成可能長さ）の最小多項式の次数は2のべき乗であることが分かる。特に、任意の構成可能点（または長さ）は代数的数であるが、すべての代数的数が構成可能というわけではない。例えば、3√2は代数^的であるが構成可能ではない。^{[ 3 ]}

構築可能な角度

構成可能な角と、任意の構成可能な円上に構成可能な点との間には、一対一の関係がある。構成可能な角は、2πを法とする加法の下でアーベル群を形成する（これは単位円上の点を複素数として見たときの乗算に対応する）。構成可能な角とは、その接線（あるいは正弦または余弦）が数として構成可能な角と同義である。例えば、正十七角形（17辺を持つ正多角形）は、以下の理由により構成可能である。

${\displaystyle {\begin{aligned}\cos {\left({\frac {2\pi }{17}}\right)}&=\,-{\frac {1}{16}}\,+\,{\frac {1}{16}}{\sqrt {17}}\,+\,{\frac {1}{16}}{\sqrt {34-2{\sqrt {17}}}}\\[5mu]&\qquad +\,{\frac {1}{8}}{\sqrt {17+3{\sqrt {17}}-{\sqrt {34-2{\sqrt {17}}}}-2{\sqrt {34+2{\sqrt {17}}}}}}\end{aligned}}}$

ガウスによって発見された。^{[ 5 ]}

構成可能な角の群は、角を半分にする演算（複素数の平方根をとる演算に相当）によって閉じている。2点から構成できる有限位数の角は、位数が2のべき乗、または2のべき乗と異なるフェルマー素数の集合との積である角のみである。さらに、無限位数の構成可能な角の稠密集合も存在する。

複素数演算との関係

ユークリッド平面上の点の集合が与えられ、そのうちの 1 つを0、別の点を1と呼び、任意の方向を選択すると、それらの点を複素数の集合として考えることができます。

点の集合を複素数として解釈する場合、有効な定規とコンパスによる構成のみを使用して構成できる点は、元の点の集合を含み、複素共役および平方根演算で閉じた最小の体の元とまったく同じです (曖昧さを避けるために、複素引数がπ 未満の平方根を指定できます)。この体の元は、加算、減算、乗算、除算、複素共役、平方根の演算のみを使用して、元の点における式として正確に表現できるもので、これは平面の可算な稠密部分集合であることが容易にわかります。これら 6 つの演算はそれぞれ、単純な定規とコンパスによる構成に対応します。このような式から、各算術演算の構成を組み合わせることで、対応する点の構成を簡単に作成できます。特定の点の集合をより効率的に構成することは、このような計算の近道に対応します。

同様に（そして2点を任意に選ぶ必要もなく）、任意の向きを与えられた場合、点の集合は、任意の2点間の差の比によって与えられる複素比の集合を決定すると言える。このような比の集合から定規とコンパスを用いて構成できる比の集合は、元の比を含み、複素共役と平方根をとらない最小の体と全く同じである。

例えば、点または比zの実部、虚部、絶対値は（上記の2つの観点のいずれかをとると）次のように表すことができるため、構成可能です。

${\displaystyle \mathrm {Re} (z)={\frac {z+{\bar {z}}}{2}}\;}$

${\displaystyle \mathrm {Im} (z)={\frac {z-{\bar {z}}}{2i}}\;}$

${\displaystyle \left|z\right|={\sqrt {z{\bar {z}}}}.\;}$

立方体の2倍角と角の3等分（φ / (2π ) )が分母が3で割り切れない有理数となるような特殊な角を除く）には、3次方程式の解となる比が必要です。一方、円の2乗には超越比が必要です。これらはいずれもここで説明する分野には含まれないため、定規とコンパスを用いた作図法は存在しません。

不可能な構造

古代ギリシャ人は、自分たちが解決できなかった建設問題は単に難解なだけで、解決不可能なものではないと考えていました。^{[ 6 ]} しかし、現代の方法では、定規とコンパスを使った建設は論理的に不可能であることが示されています。

円を四角にする

これらの問題の中で最も有名なのは、円の正方形化、または円求積法とも呼ばれる問題で、定規とコンパスだけを使用して、与えられた円と同じ面積の正方形を作成します。

円の二乗は不可能であることが証明されています。なぜなら、超越数 を生成する必要があるからです。定規とコンパスだけで構成できる代数的数は、特定の数、つまり、加算、減算、乗算、除算、そして平方根を求めるという有限の演算系列で整数から構成される数だけです。このため、「円の二乗」という表現はしばしば「不可能を可能にする」という意味で使われます。 ${\displaystyle {\sqrt {\pi }}}$

定規とコンパスだけで解くという制約がないため、この問題はさまざまな幾何学的および代数的手段で簡単に解くことができ、古代では何度も解かれてきました。^{[ 7 ]}

「円の求積法」に非常に近い近似方法は、ケプラーの三角形を使用して実現できます。

立方体を2倍にする

立方体の2倍とは、定規とコンパスだけを用いて、与えられた辺を持つ立方体の体積の2倍の体積を持つ立方体の辺を描くことです。これは不可能です。なぜなら、2の立方根は代数的ではありますが、整数から加算、減算、乗算、除算、平方根を求めることで計算することができないからです。これは、有理数上の最小多項式が3次であることに起因します。この作図は、2つの目盛りが付いた定規とコンパスを用いることで可能です。

角の三等分

角の三等分とは、定規とコンパスのみを用いて、任意の角度の3分の1の角度を作図することです。これは一般的には不可能です。例えば、2π/5ラジアン（72° = 360°/5）の角度は三等分できますが、 π /3ラジアン（60 ° ）の角度は三等分できません。^{[ 8 ]}一般的な三等分問題は、2つの目盛りが付いた定規（ニューシス作図）を使用できる場合も簡単に解けます。

楕円までの距離

平面上の任意の点から円上の最も近い点への線分は作図できますが、平面上の任意の点から正の離心率を持つ楕円上の最も近い点への線分は、 一般には作図できません。^{[ 9 ]}を参照。ここで証明された結果は、主に円錐曲線の非構成性の結果であることに注意してください。最初の円錐曲線が与えられたものとみなされる場合、他の異なる円錐曲線を生成する必要があるかどうかを確認するために証明を再検討する必要があります。例として、放物線の法線の構成は知られていますが、円と放物線自体の交点を使用する必要があります。したがって、放物線が作図できないという意味で、法線は作図できません。

アルハゼンの問題

1997年、オックスフォード大学の数学者ピーター・M・ノイマンは、古代のアルハゼン問題（ビリヤード問題または球面鏡の反射）の一般解には定規とコンパスによる構成は存在しないという定理を証明した。 ^{[ 10 ] [ 11 ]}

正多角形の構築

正五角形の構築

正多角形の中には、定規とコンパスで簡単に作図できるもの（例えば五角形）もあれば、そうでないものもあります。そこで、「すべての正多角形を定規とコンパスで作図できるのだろうか？」という疑問が生じました。

カール・フリードリヒ・ガウスは1796年に正17角形が作図可能であることを示しました。そして5年後には、nの奇数素因数が互いに異なるフェルマー素数である場合、定規とコンパスを用いて正n角形が作図可能であることを示しました。ガウスはこの条件も必要であると予想し、この予想は183​​7年にピエール・ヴァンツェルによって証明されました。 ^{[ 4 ]}

最初に作図可能な正多角形の辺の数は次のようになります。

3、4、5、6、8、10、12、15、16、17、20、24、30、32、34、40、48、51、60、64、68、80、85、96、102、120、128、136、160、170、192、204、240、255、256、257、272 ...（OEISのシーケンスA003401）​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​

偶数辺を持つ正多角形は、作図可能なものが無数に存在することが知られています（正n角形が作図可能であれば、正2n角形も作図可能であり、したがって正4n角形、正8n角形なども作図可能であるため）。しかし、フェルマー素数は5つしか知られていないため、奇数辺を持つ 正n角形は31個しか知られていません。

与えられた3つの特徴点または長さから三角形を構成する

三角形の 16 個の重要な点は、頂点、辺の中点、高さの足、内角の二等分線の足、外心、重心、垂心、内心です。これらを 3 つずつ取り上げると、3 点から三角形を構成する 139 個の重要な問題が生じます。^{[ 12 ]}これらの問題のうち 3 個では、他の 2 点から一意に構成できる点が関係します。23 個では、一意に構成できません (実際には無限個の解があります) が、それは点の位置が特定の制約に従う場合に限られます。74 個では、一般的な場合に問題が構成可能です。39 個では、必要な三角形は存在しますが、構成できません。

三角形の12の重要な長さは、3つの辺の長さ、3つの高さ、3つの中線、そして3つの角の二等分線です。これらと3つの角度を組み合わせると、95通りの組み合わせが生まれます。そのうち63通りの組み合わせは三角形を作図でき、30通りの組み合わせは作図できず、2通りの組み合わせは定義が不十分です。^{[ 13 ]：201～203ページ}

制限された構造

何を構築できるか、どのように構築できるかを決定するために、またコンパスと定規で構築できるすべてのものを構築できるようにするために必要な最小限の基準を決定するために、さまざまなルールの下で構築に許容されるツールを制限するさまざまな試みが行われてきました。

定規のみまたはコンパスのみで構築する

モール・マスケローニの定理によれば、与えられたデータと求めるデータが離散点（直線や円ではない）で構成されている限り、定規とコンパスで構築できるものはコンパスだけで構築できる。この定理の真偽はアルキメデスの公理^{[ 14 ]}の真偽に依存しており、アルキメデスの公理は一階述語ではない。コンパスのみを用いた構築の例としては、ナポレオンの問題が挙げられる。

定規だけを使った作図では、同じことは言えません。定規だけを使って平方根を取ったり、線分の中点をマークしたりすることはできません。しかし、（ポンスレ・シュタイナーの定理により）円とその中心が与えられれば、それらを描くことは可能です。

拡張された構造

古代ギリシャ人は、解くのに必要な道具の複雑さによって、作図を3つの主要なカテゴリに分類した。定規とコンパスだけを使用する作図は平面的と呼ばれ、円以外に1つ以上の円錐曲線も必要な作図は立体的と呼ばれ、3番目のカテゴリには、他の2つのカテゴリのどちらにも当てはまらないすべての作図が含まれていた。^{[ 15 ]}この分類は、現代の代数の観点とよく一致する。体の演算と平方根だけを使用して（前述 のように）表現できる複素数は平面的作図である。立方根の抽出も含む複素数は立体的作図である。

体の言葉で言えば、平面複素数は次数が2のべき乗であり、各拡大が次数2の体の塔に分解できる体の拡大に属します。立体的に構成される複素数は次数が2と3のみの素因数であり、各拡大が次数2または3の体の塔の頂点に位置する体の拡大に属します。

堅固な構造

ある点が、定規、コンパス、そして（おそらく仮想的な）円錐描画用具を用いて、焦点、準線、離心率が既に構築された任意の円錐曲線を描くことができる場合、その点は立体構築を持つ。同じ点の集合は、より少数の道具を用いて構築できる場合が多い。例えば、コンパス、定規、そして放物線y = x ²が描かれた紙と点 (0,0) および点 (1,0) を用いることで、立体構築を持つ任意の複素数を構築することができる。同様に、焦点と長軸が既に構築された任意の楕円を描くことができる道具（2本のピンと紐を想像してみてほしい）も同様に強力である。^{[ 16 ]}

古代ギリシャ人は、立方体を2倍にすることと任意の角度を3等分することはどちらも立体的な構成を持つことを知っていた。アルキメデスは正七角形のニューシス構成を提示したが、中世アラビアの注釈者バーテル・レーンダート・ファン・デル・ヴェルデンらはこれを立体的な構成に基づいていると解釈したが、他の解釈も可能であり、議論の的となっている。^{[ 17 ]}円の求積法は立体的な構成を持たない。

正n角形が立体構成を持つ場合、かつその場合のみn = 2 ^a 3 ^b mとなる。ここでaとbは非負の整数であり、mは0個以上の異なるピアポント素数（2 ^r 3 ^s + 1の形をとる素数）の積である。したがって、正n角形が立体構成を持つ場合、かつその場合のみnが次の数列に 含まれる。

7、9、13、14、18、19、21、26、27、28、35、36、37、38、39、42、45、52、54、56、57、63、65、70、72、73、74、76、78、81、84、90、91、95、97 ... （OEISの配列A051913）​​​​​​​​​​​​

正n角形が実体を持たない nの集合は、次の数列である。

11、22、23、25、29、31、33、41、43、44、46、47、49、50、53、55、58、59、61、62、66、67、69、71、75、77、79、82、83、86、87、88、89、92、93、94、98、99、100 ... （ OEISのシーケンスA048136）​​

フェルマー素数の問題と同様に、ピアポント素数が無限に存在するかどうかも未解決の問題です。

角の三等分

もし、定規とコンパスに加えて、任意の角度を（ただ）三等分できる道具があったらどうなるでしょうか？そのような作図は立体作図ですが、そのような道具では作図できない立体作図を持つ数も存在します。例えば、そのような道具では立方体を2倍にすることはできません。^{[ 18 ]} 一方、立体作図を持つすべての正n角形は、そのような道具を使って作図できます。

折り紙

折り紙の数学的理論は、定規とコンパスを用いた作図よりも強力です。藤田・羽鳥公理を満たす折り方は、コンパスと円錐描画ツールを用いた拡張作図と全く同じ点の集合を構成できます。したがって、折り紙は3次方程式（ひいては4次方程式）を解くのにも使用でき、ひいては古典問題のうち2つを解くことができます。^{[ 19 ]}

マーク可能な定規

アルキメデス、ニコメデス、アポロニウスは、目盛り付きの定規を用いた作図法を提示した。これにより、例えば、線分、2本の直線（または円）、そして1点を取り、与えられた点を通り、2本の直線と交わる線分を、交点間の距離が与えられた線分の長さに等しくなるように描くことが可能になった。ギリシャ人はこれをネウシス（「傾斜」、「傾向」、「収束」）と呼んだ。なぜなら、新しい線分は点に向かうからである。この拡張された手法では、任意の角度を三等分したり（アルキメデスの三等分法を参照）、任意の立方根を抽出したりすることができる（ニコメデスによる）。したがって、既存の距離との比が3次方程式または4次方程式の解となるような任意の距離は作図可能である。目盛り付きの定規を用いることで、7角形のような立体的な作図法を持つ正多角形を作図することができ、ジョン・H・コンウェイとリチャード・K・ガイは、それらのいくつかの作図法を提示している。^{[ 20 ]}

ニューシス構成は円錐描画ツールよりも強力で、実体構成を持たない複素数を構築できる。実際、このツールを使用すると、根号を使用しては解けないいくつかの五次方程式を解くことができる。^{[ 21 ]} ニューシス構成を使用して、7以上の素数次数の既約多項式を解くことはできないことが知られているため、このツールを使用して正23角形や29角形を構築することはできません。ベンジャミンとスナイダーは正11角形を構築できることを証明しましたが、構築方法は示していません。^{[ 22 ]} このツールを使用して正25角形や正31角形を構築できるかどうかはまだ不明です。

2進数の計算

1998年、サイモン・プラウフは、のような特定の数の2進数を計算するために使用できる定規とコンパスのアルゴリズムを発表しました。このアルゴリズムは角度の2倍計算を繰り返し行うため、20進数を超えると物理的に実行不可能になります。^{[ 23 ]}${\displaystyle \arctan(1/2)/\pi }$

参照

• カーライルサークル
• 幾何学暗号
• 幾何学
• インタラクティブな幾何学ソフトウェアのリスト。そのほとんどは定規とコンパスを使った作図を表示します。
• 紙折りの数学
• アンダーウッド・ダドリーは、定規とコンパスによる偽の証明を収集することを副業とする数学者です。

参考文献

1. ゴッドフリード・トゥーサン、「ユークリッドの第二命題の新たな考察」『数学インテリジェンサー』第15巻第3号（1993年）、12-24頁。
2. ボールド、ベンジャミン『幾何学の有名な問題とその解き方』ドーバー出版、1982年（原著1969年）。
3. ヴァンツェル、ピエール＝ローラン (1837)。「Recherches sur les moyens de reconnaître si un problème de Géométrie peut se résoudre avec la règle et le compas」(PDF)。Journal de Mathématiques Pures et Appliquées。 1. 2 : 366–372​​ 2014 年3 月 3 日に取得。
4. カザリノフ、ニコラス・D. (2003) [1970].定規と円. ミネオラ、ニューヨーク州: ドーバー. pp.  29– 30. ISBN 978-0-486-42515-3。
5. ワイスタイン、エリック W. 「三角法の角度 - Pi/17」。マスワールド。
6. スチュワート、イアン.ガロア理論. p. 75.
7. 「円を四角にする」 www-gap.dcs.st-and.ac.uk/ JJ O'ConnorとEF Robertson。 2017年6月25日時点のオリジナルよりアーカイブ。
8. 72 度の角度を三等分するための手順。
9. Azad, H., Laradji, A.、「初等幾何学におけるいくつかの不可能な構成」、 Mathematical Gazette 88、2004年11月、548-551。
10. ノイマン、ピーター・M. (1998)、「球面鏡における反射の反射」、アメリカ数学月刊誌、105 (6): 523– 528、doi : 10.1080/00029890.1998.12004920、JSTOR 2589403、MR 1626185  
11. Highfield, Roger (1 April 1997) 「ドンは古代ギリシャ人が残した最後のパズルを解く」Electronic Telegraph 676 、 2004年11月23日時点のオリジナルよりアーカイブ、 2008年9月24日閲覧。
12. Pascal Schreck, Pascal Mathis, Vesna Marinkoviċ, Predrag Janičiċ. "Wernick's list: A final update", Forum Geometricorum 16, 2016, pp. 69–80. http://forumgeom.fau.edu/FG2016volume16/FG201610.pdf 2016年4月8日アーカイブ、Wayback Machineにて
13. ポサマンティエ、アルフレッド・S.、レーマン、イングマール『三角形の秘密』プロメテウス・ブックス、2012年。
14. アヴロン、アーノン(1990). 「コンパスのみを用いた厳密な強構成可能性について」. Journal of Geometry . 38 ( 1–2 ): 12–15 . doi : 10.1007/BF01222890 . S2CID 1537763 . 
15. TL Heath、「ギリシャ数学史 第1巻」
16. P. Hummel、「楕円を用いた立体構成」、 The Pi Mu Epsilon Journal、 11 (8)、429-435 (2003)
17. クノール、ウィルバー・R. (1989)、「アルキメデスによる正七角形の構築について」、ケンタウラス、32 (4): 257– 271、Bibcode : 1989Cent...32..257K、doi : 10.1111/j.1600-0498.1989.tb00848.x、MR 1078083 
18. グリーソン、アンドリュー：「角の三等分、七角形、そして三十角形」 アメリカ数学月刊95（1988）、第3号、185-194ページ。
19. ロウ、T. スンダラ (1966). 『折り紙の幾何学的演習』 ニューヨーク: ドーバー.
20. コンウェイ、ジョン・H.、リチャード・ガイ著『民数記』
21. A. Baragar、「2回刻み目の定規を使用した構成」、アメリカ数学月刊、 109 (2)、151-164 (2002)。
22. ベンジャミン、エリオット；スナイダー、C. (2014). 「目盛り付き定規とコンパスによる正12角形の構築について」.ケンブリッジ哲学協会数学紀要. 156 (3): 409– 424. Bibcode : 2014MPCPS.156..409B . doi : 10.1017/S0305004113000753 .
23. Simon Plouffe (1998). 「定規とコンパスを用いた特定の数の計算」 . Journal of Integer Sequences . 1 : 13. Bibcode : 1998JIntS...1...13P . ISSN 1530-7638 . 

外部リンク

• ドレクセル大学の数学フォーラムにおける数学博士による正多角形の構築
• コンパスを使った建設は、結び目を切るだけで完了します
• ヒポクラテスによる結び目の切断における角度の三等分
• ワイスタイン、エリック W. 「角の三等分」。マスワールド。