アフィン微分幾何学

微分幾何学において、アフィン微分幾何学はアフィン変換を受ける多様体の幾何学的不変量を研究する分野であり、等アフィン微分幾何学は体積保存アフィン変換を受ける多様体の幾何学的不変量を研究する分野です。同様に、アフィン微分幾何学はアフィン接続（通常は捩れがないと仮定）を備えた滑らかな多様体であるアフィン多様体を研究する分野であり、等アフィン微分幾何学はどこにも消滅しない体積形式を備えたアフィン多様体を研究する分野です。

球面、円筒面、双曲面など、任意の (擬似) リーマン多様体が自動的にアフィン多様体となるため、アフィン多様体の例は数多くあります。ただし、任意の (擬似) リーマン多様体によって誘導されないアフィン多様体も存在します。

直感的に言えば、共形幾何学は角度が不変となるアフィン幾何学であり、アフィン幾何学は角度が柔軟となる共形幾何学です。リーマン幾何学と比較すると、特殊アフィン幾何学は計量ではなく体積形式を備えた多様体を研究します。シンプレクティック幾何学は、特殊アフィン幾何学とリーマン幾何学の中間の硬さを持ちます。

アフィン微分幾何学という名称は、クラインのエルランゲンプログラムに由来します。

平面上のアフィン幾何学

このセクションは^{[ 1 ]}^{[ 2 ]に基づいています。}

アフィン微分幾何学の最も単純なケースでは、アフィン平面における曲線の微分特性を調べます。つまり、のアフィン変換に対して不変であるにおける曲線の特性を調べます。多くの特性は、面積保存アフィン変換に対してのみ不変です。これらの特性は等アフィンであり、アフィンではありません。ただし、等アフィン特性は、本質的に長さのスケールが固定されたアフィン特性であるため、等アフィン幾何学とアフィン幾何学の間で変換を行うことができます。たとえば、厳密に凸で滑らかな曲線の等アフィン弧長は明確に定義されているため、2 つの厳密に凸で滑らかな曲線間のアフィン弧長比も明確に定義されています。 $\mathbb {A} ^{2}$ $\mathbb {R} ^{2}$ $\mathbb {R} ^{2}$

このセクションの残りの部分では、連続した 4 次導関数を持つ曲線のみを考慮します。

アフィン正規分布

{\displaystyle y=x^{2}-3x^{3}} — のアフィン中点構成。中点はを描きます。 $y=x^{2}-3x^{3}$ $x={\tfrac {3}{2}}y+O(y^{1.5})$

{\displaystyle y=x^{2}-100x^{5}} — のアフィン中点構成。中点はを描きます。 $y=x^{2}-100x^{5}$ $x=50y^{2}+O(y^{2.5})$

放物線のアフィン法線はその軸である。曲線上の凸点を通る アフィン法線は、接触放物線の軸である。同様に、接触放物線は中点によって構成される。

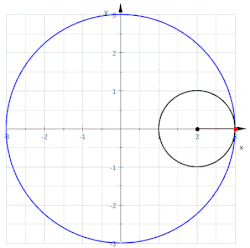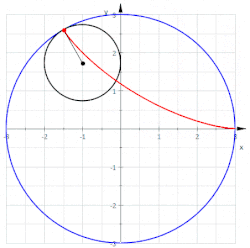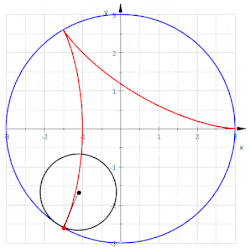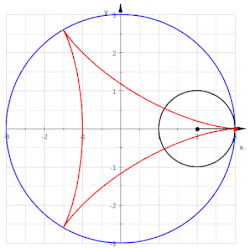
をに厳密に凸な点を持つ曲線とすると、その点におけるアフィン法線は、接線に平行な直線を用いて曲線をの近くで切断することによって得られる。これにより線分の族が得られる。これらの線分の中点は別の曲線をなぞる。アフィン法線は、における中点軌跡の接線である。^[³^] $x(t)$ $t=0$ $x(0)$ $(x(0),{\dot {x}}(0))$ $x(0)$

{\displaystyle r=1+\epsilon \cos(3\theta )} — のアフィン焦点集合。これは三角曲線に収束する。 $r=1+\epsilon \cos(3\theta )$ $\epsilon \downarrow 0$

{\displaystyle y^{2}=x^{3}+x^{2}} — 楕円曲線のアフィン焦点集合。 $y^{2}=x^{3}+x^{2}$

詳細には、で指定された曲線がある場合、における中点曲線の傾きはで決定され、その湾曲は高次の係数などによって決定されます。放物線のアフィン変換により、放物線の軸を曲線に一致させることができます。 $x_{1}(t)=t,\;x_{2}(t)={\frac {1}{2}}x_{2}''(0)t^{2}+{\frac {1}{6}}x_{2}^{(3)}(0)t^{3}+\cdots$ $(0,0)$ $x_{2}^{(3)}(0)$

アフィン法線の包絡線はアフィン焦点集合である。放物線のアフィン焦点集合は、その軸の無限遠点である。同様に、楕円と双曲線のいずれの場合も、アフィン焦点集合は一点に縮退する。一般に、アフィン焦点集合が一点となるのは、曲線が円錐曲線である場合に限る。

アフィン幾何学において、円錐曲線の焦点は等アフィン変換に対して不変ではないため、意味のある概念ではないことに注意してください。したがって、「焦点」という言葉が使用される場合、それはアフィン焦点集合を指します。

一般的に

同様に、3次元空間の滑らかな曲面について、その接平面をずらしながら、ある点におけるデュパン示線条を考えてみましょう。その点が楕円点であれば、接平面は楕円列を切断し、アフィン法線は楕円の中心によって張られます。同様に、その点が双曲点である場合も同様です。これはn次元空間の超曲面へと一般化されます。

線要素

線分要素とは、特定の点を持つ直線と定義します。線分要素はで表され、は非零の実数を乗じた場合のみ定義されます。ここで、2次元平面上の線分要素は、3次元空間上の点とみなせることを示します。 $(x,v)$ $x,v\in \mathbb {R} ^{2}$ $v$ $\mathbb {R} ^{2}$ $\mathbb {P}$

における任意の2つの放物線に対して、一方を他方に写す等アフィン変換が存在する。したがって、ユークリッド微分幾何学における接線を用いた多くの構成は、接触放物線を用いたアフィン微分幾何学における構成に変換できる。 $\mathbb {R} ^{2}$

一般的な位置にある任意の4本の直線には、それら4本すべてに接する唯一の放物線が存在する。したがって、任意の2本の線分要素に対して、両方の点において唯一の放物線が存在する。それに接するすべての線分要素の1パラメータ族は、における直線である。 $(x,v),(x',v')$ $x,x'$ $\mathbb {P}$

パラメータ化された曲線が与えられた場合、任意の点において、曲線をの形に変換するユークリッド変換が存在します。言い換えれば、曲線は長さ1のの標準形を持ちます。ベクトルは符号を除いて一意です。 $x(t)$ $t_{0}$ $t\mapsto (t,{\tfrac {1}{2}}kt^{2}O(t^{3}))$ $x(t_{0}+t)=e_{0}t+{\tfrac {1}{2}}{\ddot {x}}(0)t^{2}+\cdots$ $e_{0}$ $e_{0}$

これは、では、次数 2 で交差する唯一の直線が存在し、のべき乗展開で 2 つの項が消去されるためです。 $x(t_{0})$ $x(t)$ $x(t)$

同様に、無限に近接した2点でに接する放物線が存在します。これは4次の接線であることを意味し、のべき乗展開における4つの項が消去されます。したがって、曲線をの形に変換する等アフィン変換が存在します。言い換えれば、、、が面積1の平行四辺形を張るような2つのベクトルが存在するということです。このペアはの符号を除いて一意です。 $x(t)$ $x(t)$ $t\mapsto (t,{\tfrac {1}{2}}t^{2}+O(t^{4}))$ $e_{0},e_{1}$ $x(t_{0}+t)=x(t_{0})+e_{0}t+{\tfrac {1}{2}}e_{1}t^{2}+{\tfrac {1}{24}}x^{(4)}(t_{0})t^{4}+\cdots$ $e_{0},e_{1}$ $e_{0},e_{1}$ $e_{0}$

以降、これを等アフィンパラメータ化と呼ぶことにします。

等アフィン弧長

{\displaystyle 2(dA)^{1/3}} — 等アフィン弧長はを積分することによって計算されます。ここで、は描画される無限小三角形の面積です。 $2(dA)^{1/3}$ $dA$

面積は等アフィン幾何学において不変であるため、互いに平行でない2本の線分が与えられた場合、それらは三角形を形成します。これらの線分間の距離は三角形の面積のと定義します。2本の線分が平行となる退化したケースでは、それらの距離は定義されません。における面積は等アフィン変換において不変であるため、における計量も不変です。において、の指数は放物線の加法的な性質により必要ですが、の係数は方程式を単純化するための慣例的なものであることに注意してください。 $(x,v),(x',v')$ $d((x,v),(x',v'))$ $2A^{1/3}$ $\mathbb {R} ^{2}$ $\mathbb {P}$ $2A^{1/3}$ $1/3$ $2$

したがって、連続する接線によって形成される無限小三角形を積分することによって、厳密に凸状の曲線上の等アフィン弧長について話すことができ、これにより等アフィンパラメータ化を定義できるようになります。

等アフィンパラメータ化を生成する別の方法があります。パラメータ化がユークリッド弧長である場合、ベクトルの長さは単位です。同様に、パラメータ化が等アフィン弧長である場合、2つのベクトルがすべてのに対して単位面積の平行四辺形を張る場合、その場合にのみ等アフィン弧長となります。 $x(t)$ ${\dot {x}}(t)$ $x(t)$ ${\dot {x}}(t),{\ddot {x}}(t)$ $t$

放物線上の加法性

{\displaystyle 2A^{1/3}} — 放物線上の加法性。 $2A^{1/3}$

座標において、次のパラメータ化された放物線を考えます。放物線は点を通り、接線はの方向、軸はの方向にあります。 $x(t)=x_{0}+{\dot {x}}_{0}t+{\frac {1}{2}}{\ddot {x}}_{0}t^{2}$ $x_{0}$ ${\dot {x}}_{0}$ ${\ddot {x}}_{0}$

放物線上の2点を考えます。2本の接線は三角形を形成します。直接計算すると、三角形の面積はです。これは、放物線に沿った2本の線分要素が与えられている場合、次の式が成り立つことを意味します。等アフィン弧長は、同じ放物線を細分化しても不変です。つまり、等アフィン弧長は、細分化を細かくしていくと、明確に定義された極限に収束します。 $x(t_{1}),x(t_{2})$ $A={\tfrac {1}{8}}(t_{2}-t_{1})^{3}|{\dot {x}}_{0}\times {\ddot {x}}_{0}|$ $(x(t_{1}),{\dot {x}}(t_{1})),(x(t_{2}),{\dot {x}}(t_{2}))$ $d((x(t_{1}),{\dot {x}}(t_{1})),(x(t_{2}),{\dot {x}}(t_{2})))=(t_{2}-t_{1})|{\dot {x}}_{0}\times {\ddot {x}}_{0}|^{1/3}$

特に、これは放物線のアフィン媒介変数化であることがわかります。をアフィンスケーリングすると、等アフィン媒介変数化になります。 $t$

特に、は等アフィンパラメータ化です。 $t\mapsto (t,{\tfrac {1}{2}}t^{2})$

等アフィン曲率

等アフィン弧長構成は、曲線を接触放物線の列として近似することに依存しています。明らかに、放物線の接触放物線は放物線そのものです。しかし、一般的な厳密凸曲線の場合、接触放物線は弧長に応じて変化します。これは等アフィン幾何学における曲率を定義するために使用できます。

ユークリッド媒介変数化において、はに垂直なので、はによって定義される自然な媒介変数化を持ちます。ここでは、単位速度ベクトルの回転速度です。つまり、は時計回りに直角回転した状態です。 ${\ddot {x}}$ ${\dot {x}}$ $\kappa (t)$ $\kappa (t)$ ${\ddot {x}}(t)=\kappa (t){\dot {x}}^{\perp }(t)$ ${\dot {x}}^{\perp }(t)$ ${\dot {x}}(t)$

同様に、等アフィンパラメータ化では、はに平行なので、によって定義される自然なパラメータ化を持ちます。ここで、はそのアフィン法線がせん断される速度です。量は等アフィン曲率です。 $x^{(3)}$ ${\dot {x}}$ $\kappa (t)$ $\kappa (t)$ $x^{(3)}(t)+k(t){\dot {x}}(t)=0$ $k(t)$

放物線はを満たす唯一の曲線です。その等アフィンパラメータ化はです。これは、放物線の曲率がゼロであるため、放物線が直線に相似であることを示しています。 $k=0$ $(t,{\tfrac {1}{2}}t^{2})$

楕円は、正の曲率が一定である唯一の曲線です。その等アフィンパラメータ化は、またはそれと同値で、面積はです。 $k>0$ ${\begin{cases}&x_{1}=a\cos(k)^{1/2}t,\;x_{2}=b\sin(k)^{1/2}t,\\&{\frac {x_{1}^{2}}{a^{2}}}+{\frac {x_{2}^{2}}{b^{2}}}=1,\;k=(ab)^{-2/3}.\end{cases}}$ $k=(\pi /A)^{2/3}$ $A$

を持つ双曲線は、負の定曲率を持つ唯一の曲線です。その等アフィンパラメータ化はです。曲線のある点におけるユークリッド曲率は、次数3の接触円を一意に見つけることによって得られます。同様に、アフィン曲率は次数5の接触円錐曲線を一意に見つけることによって得られます。 $k<0$ ${\begin{cases}&x_{1}=a\cosh(-k)^{1/2}s,\;x_{2}=b\sinh(-k)^{1/2}s,\\&{\frac {x_{1}^{2}}{a^{2}}}-{\frac {x_{2}^{2}}{b^{2}}}=1,\;k=-(ab)^{-2/3}.\end{cases}}$

等アフィン曲率が一般的な局所的最大値または最小値に達すると、対応する焦点は半立方体の尖点に達します。

空間におけるアフィン幾何学

をパラメータ化されたサーフェスとします。 $M$ $M\subset \mathbb {R} ^{3}$

正規形

一般的な楕円点では、表面は等アフィン変換によって次の正規形に変換できます。または円筒座標では、です。 $x\in M$ $z={\frac {1}{2}}(x^{2}+y^{2})+{\frac {c}{6}}(x^{3}-3xy^{2})+\cdots$ $z={\tfrac {1}{2}}\rho ^{2}+c\rho ^{3}\cos(3\varphi )+O(\rho ^{4})$

この変換を得るには、まずユークリッド変換を行い、接平面を平面に移動し、デュパン示線条体の2つの軸を方向に向けます。次に、方向に体積保存伸張を行います。言い換えれば、曲面は局所的にはモンキーサドルによって変形された放物面です。 $z=0$ $x,y$ $x,y,z$

放物面軸の周りを 60° 回転させるとの符号が反転するため、等アフィン幾何学ではのみが明確に定義された量となります。 $c$ $c^{2}$

2パラメータ平面族が存在する。一般に、各平面はにおいて等アフィン曲率を持つ曲線で曲面と交差する。これは対応する等アフィン断面曲率である。 $x$

各単位ベクトルに対し、の近傍に同じ方向の2パラメータ直線族が存在する。一般に、各直線は2点で交差し、それらの中点はを通る曲面を形成する。における接平面は、直線要素に対応するトランソン平面である。単位ベクトルが回転すると、1パラメータトランソン平面族が掃引される。これらの平面の包絡面は、を頂点とする三角錐曲線円錐であり、内接楕円を持つ。これは、楕円臍線の焦点面と関連している。 $v\in T_{x}M$ $x$ $M$ $x$ $x(u_{0},v_{0})$ $(x,v)$ $x$

三角錐の中心線は、における表面のアフィン法線です。 $x$

{\displaystyle z={\tfrac {1}{2}}\rho ^{2}+c\rho ^{3}\cos(3\varphi)+O(\rho ^{4})} — 下の図は、2つのデュパン示線を示しており、1つは、もう1つはである。これらは3本の直線で交差し、3本のダルブー接線となる。これらは3本のセグレ接線と双対である。上の図は、対応する三角錐を示しており、6つのトランソン平面が6本の直線で示されている。3本のダルブー接線は、3つの三角錐尖を通る3本の直線に対応し、3本のセグレ接線は、内接円に接する3本の直線に対応する。 $z={\tfrac {1}{2}}\rho ^{2}+c\rho ^{3}\cos(3\varphi )+O(\rho ^{4})$ $z={\tfrac {1}{2}}\rho ^{2}$

三角錐上では、6つの点が特殊です。3つの尖点と、その内接楕円の3つの接線です。これらは6つのトランソン平面に対応し、トランソン平面は（尖点の） 3つのダルブー接線と、における曲面の3つのセグレ接線に対応します。 $x$

3つのダルブー接線は、最も接触する放物面との交点から求めることもできます。交点は傘のような形をしており、3対の棘状の突起が3つのダルブー接線となります。 $z={\tfrac {1}{2}}\rho ^{2}+c\rho ^{3}\cos(3\varphi )+O(\rho ^{4})$ $z={\tfrac {1}{2}}\rho ^{2}$

ブラシュケ計量

各楕円点において、曲面をその通常の形状に変換する等アフィン変換は（120°回転まで）1つだけ存在するため、等アフィン幾何学において正定値二次形式は明確に定義される。これはブラシュケ計量、またはベルワルド・ブラシュケ計量と呼ばれる。 $z={\frac {1}{2}}(x^{2}+y^{2})+{\frac {c}{6}}(x^{3}-3xy^{2})+\cdots$ $ds^{2}=dx^{2}+dy^{2}$

曲面上の曲線が与えられた場合、その曲線に沿ってブラシュケ計量を積分すると、先に構築した等アフィン弧長と同じ結果が得られます。したがって、曲面の等アフィン幾何学の計量構造はリーマン幾何学の計量構造と同じですが、これによって等アフィン幾何学がリーマン幾何学に還元されるわけではありません（後述）。

ブラシュケ計量は、曲面を通常の形に変換することなく定義することもできます。がにおける滑らかで局所的に厳密凸な超曲面であるとし、ある点の近傍で曲面が関数のグラフであるとすると、ブラシュケ計量はとなり、はの範囲にあります。この定義は、周囲空間の等アフィン変換に対して不変です。 $M$ $\mathbb {R} ^{n+1}$ $x^{0}=f(x^{1},\dots ,x^{n})$ $ds^{2}=|\det[\partial _{ij}f]|^{-{\frac {1}{n+2}}}\partial _{ij}f\;dx^{i}dx^{j}$ $i,j$ $1:n$ $\mathbb {R} ^{n+1}$

没入型多様体視点

リーマン幾何学は、をリーマン多様体とみなし、に多様体を浸すことで研究できる。同様に、アフィン微分幾何学は、をアフィン多様体とみなし、に多様体を浸すことで研究できる。 $\mathbb {R} ^{n}$ $\mathbb {R} ^{n}$

アフィン基本形式

ユークリッド空間における曲面の場合、2つの基本形式、すなわち第1基本形式と第2基本形式が存在します。第1基本形式は誘導リーマン計量であり、曲面の固有の計量構造を記述します。第2基本形式は外在幾何学を記述し、曲面上の共変微分（すなわち平行移動）をによって定義するために使用できます。ここでは周囲のユークリッド空間における共変微分（すなわち標準微分）です。第2基本形式は、曲面の接平面と接平面に垂直な直線という2つの部分空間に分割することによって得られます。 $\nabla _{X}Y=\nabla _{X}^{\text{ext}}Y-\mathrm {I\!I} (X,Y)$ $\nabla _{X}^{\text{ext}}Y$ $\nabla _{v}^{\text{ext}}w$

アフィン幾何学においても、第二基本形式と同様の構成法がある。をにおける局所的に厳密な凸面とする。各点において、がを横断するような部分空間を定義する。すると、上のベクトル場の任意の対をにおいて部分的に定義されたベクトル場とみなすと、ベクトル場はのように分解される。をの成分として定義する。はこれに関連付けられたアフィン基本形式であり、によって対応する共変微分を定義する。 $M$ $\mathbb {R} ^{n+1}$ $x\in M$ $N_{x}\subset T_{x}\mathbb {R} ^{n+1}$ $T_{x}M$ $X,Y$ $M$ $\mathbb {R} ^{n+1}$ $\nabla _{X}^{\text{ext}}Y$ $N\oplus TM$ $\alpha (X,Y)$ $N$ $\alpha$ $\nabla _{X}Y=\nabla _{X}^{\text{ext}}Y-\alpha (X,Y)$

が1次元で、面が向き付け可能な場合、零でない横ベクトル場を選び、によって双線型形式を定義することができます。これは正定値であり、再びリーマン多様体になります。 $N_{x}$ $v$ $h(X,Y)$ $\alpha (X,Y)=h(X,Y)v$ $M$

によって定義される(1, 1)-テンソルであるアフィン形状演算子もあります。 $S(X)=-\nabla _{X}^{\text{ext}}v$

の多くの選択肢のうち、アンビエントのアフィン幾何学は、アフィン法線を特別なものとして選びます。アフィン法線が用いられる場合、の誘導共変微分はブラシュケ接続です。抽象的に言えば、これはアフィン多様体のはめ込みです。 $N$ $\mathbb {R} ^{n+1}$ $\nabla ^{\text{Bla}}$ $M\subset \mathbb {R} ^{n+1}$

には自然な長さのスケールが存在しないため、はまだ明確に定義されていないことに注意してください。しかし、周囲空間を単なるアフィン空間ではなく、等アフィン空間とみなせば、自然な長さのスケールが存在します。具体的には、任意のの近傍において、の等アフィン変換が存在し、その面はの正規形となります。次に、その点におけるベクトルを単に取ります。これを用いると、等アフィン多様体の浸漬が得られます。 $h(X,Y)$ $N$ $\mathbb {R} ^{n+1}$ $p\in M$ $\mathbb {R} ^{n+1}$ $x^{0}={\frac {1}{2}}\sum _{i=1}^{n}(x_{i})^{2}+\cdots$ $\partial _{x^{0}}|_{p}$

ガウス・コダッツィ方程式のような曲面の微分幾何学における多くの方程式は、アフィン形状演算子とアフィン基本形を用いたアフィン幾何学において直接類似している。^{[ 4 ]}^{：第II.3節}

ある点においては、形状作用素は恒等式となることがある。そのような点は臍点と呼ばれる。すべての点が臍点となるアフィン多様体はアフィン球面と呼ばれる。

ブラシュケ構造

はリーマン計量とブラシュケ接続の両方を持つが、によって誘導されるレヴィ・チヴィタ接続は一般にとは異なることに注意されたい。一方、は一般にである。(0, 3)テンソル、すなわち3次形式は一般に非ゼロである。ピックとベルワルドの古典的な定理によれば、は非退化であり、が2次曲面である場合に限る。 ^[⁴^]^：第2.3節 $M$ $h$ $\nabla ^{\text{Bla}}$ $\nabla ^{h}$ $h$ $\nabla ^{\text{Bla}}$ $\nabla ^{h}h=0$ $\nabla ^{\text{Bla}}h\neq 0$ $C(X,Y,Z):=\nabla _{X}^{\text{Bla}}(h(Y,Z))$ $h$ $C=0$ $M$

一般に、非退化双線型形式を備えた抽象アフィン多様体を考える。すると、は共役アフィン接続を生成する。そしての場合、のレヴィ・チヴィタ接続も同様である。 $(M,\nabla )$ $h$ ${\bar {\nabla }}$ $Xh(Y,Z)=h(\nabla _{X}Y,Z)+h(Y,{\bar {\nabla }}_{X}Z)$ ${\tfrac {1}{2}}(\nabla +{\bar {\nabla }})h=0$ ${\tfrac {1}{2}}(\nabla +{\bar {\nabla }})$ $h$

抽象的な多様体の視点

リーマン幾何学が曲線と曲面のユークリッド微分幾何学の一般化であるのと同様に、アフィン微分幾何学は曲線と曲面のアフィン微分幾何学の一般化です。

ここでは最も単純な場合、すなわち余次元1の多様体を考える。を次元多様体とし、をに横切るベクトル場とし、すべてのに対してとなるものとする。ここでは直和、線形スパンを表す。 $M\subset \mathbb {R} ^{n+1}$ $n$ $\xi$ $\mathbb {R} ^{n+1}$ $M$ $T_{p}\mathbb {R} ^{n+1}=T_{p}M\oplus {\text{Span}}(\xi )$ $p\in M$ $\oplus$ ${\text{Span}}$

滑らかな多様体、たとえばNについて、 Ψ( N ) をN上の滑らかなベクトル場の加群とします。D : Ψ( R ⁿ⁺¹ )×Ψ( R ⁿ⁺¹ ) → Ψ( R ⁿ⁺¹ )をR ⁿ⁺¹上の標準共変微分とし、 D ( X , Y ) = D _X Yとします。D _X Y は、 Mに接する成分と、 ξ に平行な横方向成分に分解できます。これにより、ガウスの方程式: D _X Y = ∇ _X Y + h ( X , Y )ξが得られます。ここで、 ∇ : Ψ( M )×Ψ( M ) → Ψ( M )はM上の誘導接続であり、h : Ψ( M )×Ψ( M ) → Rは双線型形式です。 ∇ とh は横方向ベクトル場 ξ の選択に依存することに注意してください。ここでは、 hが非退化である超曲面のみを考察する。これは超曲面Mの性質であり、横ベクトル場 ξ の選択には依存しない。^[⁴^] hが非退化であるとき、 Mは非退化であるという。平面上の曲線の場合、非退化曲線とは変曲点を持たない曲線のことである。3次元空間上の曲面の場合、非退化曲面とは放物点を持たない曲面のことである。

ξ の接線方向、例えばXにおける微分も考えられます。この量D _X ξ は、 Mに接する成分と、 ξ に平行な横成分に分解できます。これにより、 Weingarten方程式が得られます：D _X ξ = − SX + τ( X )ξ。 (1,1)型テンソルS : Ψ( M ) → Ψ( M )はアフィン形状演算子と呼ばれ、微分一形式τ : Ψ( M ) → Rは横接続形式と呼ばれます。ここでも、Sと τ は横ベクトル場 ξ の選択に依存します。

最初の誘導ボリュームフォーム

Ω : Ψ( R ^{n +1} ) ^{n +1} → RをR ⁿ⁺¹上で定義された体積形式とします。ω : Ψ( M ) ⁿ → Rで与えられるM上の体積形式はω( X ₁ ,..., X _n ) := Ω( X ₁ ,..., X _n ,ξ)で与えられます。これは自然な定義です。ユークリッド微分幾何学において、ξ をユークリッド単位法線とすると、 X ₁ ,..., X _nが張る標準ユークリッド体積は常に ω( X ₁ ,..., X _n )に等しくなります。ω は横ベクトル場 ξ の選択に依存することに注意してください。

2番目の誘導体積形式

接ベクトルX ₁ ,..., X _nについて、H := ( h _i,j )をh _i,j := h ( X _i , X _j )で与えられるn × n行列とします。M上の 2 番目の体積形式をν : Ψ( M ) ⁿ → Rで定義します。ここでν( X ₁ ,..., X _n ) := |det(H)| ¹^⁄²です。これも自然な定義です。M = R ⁿでhがユークリッドスカラー積の場合、 ν( X ₁ ,..., X _n ) は常にベクトルX ₁ ,..., X _nが張る標準ユークリッド体積です。 h は横ベクトル場 ξ の選択に依存するため、 ν もそれに依存します。

2つの自然条件

我々は2つの自然な条件を課す。1つ目は、誘導接続 ∇ と誘導体積形式 ω が両立すること、すなわち ∇ω ≡ 0 であることだ。これは、すべてのX ∈ Ψ( M )について∇ _X ω = 0となることを意味する。言い換えれば、ベクトルX ₁ ,..., X _nを接続 ∇ に関してM内のある曲線に沿って平行移動させると、体積形式 ω に関してX ₁ ,..., X _nが張る体積は変化しない。直接計算^[⁴^]により、 ∇ _X ω = τ( X )ωとなり、したがってすべてのX ∈ Ψ( M ) について∇ _X ω = 0となるのは、 τ ≡ 0 の場合、すなわちすべてのX ∈ Ψ( M )についてD _X ξ ∈ Ψ( M )となる場合のみであることが分かる。これは、ξ を接線方向XでDに関して微分すると、常にMへの接線ベクトル（場合によってはゼロ）が得られることを意味します。2つ目の条件は、2つの体積形式 ω と ν が一致すること、すなわちω ≡ ν であることです。

結論

^{[ 4 ]}から、符号を基準として、∇ω ≡ 0とω ≡ νという 2 つの条件が両方とも満たされる横ベクトル場 ξ の唯一の選択が存在することが示せます。これら 2 つの特殊な横ベクトル場は、アフィン法線ベクトル場、またはBlaschke法線場と呼ばれることもあります。 ^{[ 1 ]}定義が体積形式に依存することから、アフィン法線ベクトル場は体積を保存するアフィン変換に対して不変であることがわかります。これらの変換はSL( n +1, R ) ⋉ R ^{n +1}で与えられます。ここで SL( n +1, R ) は、実数要素と行列式 1 を持つ( n +1) × ( n +1)行列の特殊線型群を表し、⋉ は半直積を表します。SL( n +1, R ) ⋉ R ⁿ⁺¹はリー群を形成します。

構造

このセクションは^{[ 5 ]}^{[ 4 ]に基づいています。}

便宜上、多様体はパス接続されていると常に仮定します。そうでない場合は、各コンポーネントを個別に調査できるためです。

平坦アフィン幾何学

$\mathbb {A} ^{n}$ はアフィン幾何学とみなされます。平坦、つまり曲率が0です。 $\mathbb {R} ^{n}$

それぞれに対して、 k単体、k楕円体、k平行体がそれぞれ1 つずつ存在します。 $k=1,2,\dots ,n$

線分の長さは定義されないが、同一直線上にある2つの有向線分の長さの比は明確に定義されている。同様に、2つの平行平面間の距離は明確に定義されないが、有向線分間の距離の比は明確に定義されている。

コンパクトサブセットの重心は明確に定義されています。

測地線

アフィン多様体はアフィン接続（デフォルトでは捩れのないと仮定）を持ち、と表記できます。これにより、リーマン幾何学にも現れる多くの構造を定義できます。まず、共変微分または平行移動はによって定義され、これは本質的に接続自体と等価です。これにより、がに平行となるような曲線として測地線を定義できます。すべての測地線には、変数のアフィン変換を除いて一意のアフィンパラメータ化があります。 $(M,\nabla )$ $\nabla$ $\gamma$ $\nabla _{\dot {\gamma }}{\dot {\gamma }}$ ${\dot {\gamma }}$

アフィン媒介変数化は、より簡潔に言えばを満たす。アフィン媒介変数化を用いると、測地線上の2つの有向線の比は明確に定義される。したがって、測地線はアフィン直線の直線埋め込みと考えることができる。なお、曲線が測地線でない場合、等速曲線について語ることは一般に意味がない。なぜなら、同じアフィン直線上にない2つのベクトルの長さの比を比較することはできないからである。 $\nabla _{\dot {\gamma }}{\dot {\gamma }}=0$ ${\ddot {\gamma }}=0$ $\mathbb {A} ^{1}$

測地線が完全とは、それが常に前方および後方に拡張される場合に限ります。つまり、型のアフィンパラメータ化を持ちます。そのすべての測地線が完全であれば、は測地的に完全です。それを完全化する方法がない場合、つまりとなるような測地的に完全なアフィン多様体が存在しない場合、は本質的に測地的に不完全です。 $\mathbb {R} \to M$ $(M,\nabla )$ ${\bar {M}}$ $M\subset {\bar {M}}$ $M$

任意の点および任意の方向において、となる一意のアフィンパラメータ化された測地線が存在する。したがって、定数を任意に固定すると、写像は指数写像を定義し、これはゼロの開近傍を自身に写像する。の正確な選択は重要ではないが、リーマン多様体の場合とは異なり、接空間上の距離を測定する自然な方法がないため、一般に自然な選択はない。便宜上、を任意に固定し、指数写像をと定義する。 $x\in M$ $v\in T_{x}M$ $\gamma$ $\gamma _{v}(0)=x,\;{\dot {\gamma }}_{v}(0)=v$ $t_{0}>0$ $v\mapsto \gamma _{v}(t_{0})$ $T_{x}M$ $M$ $t_{0}$ $t_{0}=1$ $\exp _{x}(v)=\gamma _{v}(1)$

殺害

アフィンキリングベクトル場は、アフィン接続を保存するベクトル場です。つまり、であり、はリー微分です。特に、無限小平行四面体は、キリングベクトル場の下を流れるときも平行四面体のままです。リー括弧で囲まれた上のアフィンキリングベクトル場の集合は、リー代数を形成します。 $X$ ${\mathcal {L}}_{X}(\nabla )=0$ ${\mathcal {L}}$ $(M,\nabla )$ $[\cdot ,\cdot ]$ ${\mathfrak {K}}(M,\nabla )$

ベクトル場が完備であるためには、積分曲線が常に存在する必要がある。完備なキリングベクトル場は、それ自身への1パラメータのアフィン微分同相写像族を生成する。 $M$

$(M,\nabla )$ は、すべてのアフィンキリングベクトル場が完全である場合に限り、 アフィンキリング完全です。

自身に写像するアフィン微分同相写像群はである。これは有限次元リー群である。そのリー代数はのリー部分代数であり、アフィンキリング完備ベクトル場から構成される。^[⁵^] $(M,\nabla )$ $\operatorname {Aff} (M,\nabla )$ ${\mathfrak {aff}}(M,\nabla )$ ${\mathfrak {K}}(M,\nabla )$

モルフィズム

アフィン微分同相写像は、アフィン接続を保存する微分同相写像です。局所アフィン微分同相写像は、開集合のみに制限されたアフィン微分同相写像です。

アフィン被覆写像は、任意のアフィン多様体が開近傍を持ち、その近傍がアフィン微分同相写像に制限されるような2 つのアフィン多様体間の関数です。 $f:M\to N$ $x\in M$ $f$

アフィン多様体は、任意の2点に対してへの（局所）アフィン微分同相写像が存在する場合にのみ、（局所）対称である。例えば、任意の（局所）対称擬リーマン空間は、アフィン多様体として自動的に（局所）対称となる。 $x,y\in M$ $x$ $y$

直感的に言えば、局所対称多様体とは、その中のどの点に立ってそこから外を眺めても、自分がどこにいるのか分からない（ただし、大域幾何学が作用するほど遠くを見ない限りは）多様体です。同様に、対称多様体とは、その中のどの点に立って外を眺めても、どれだけ遠くを見渡しても自分がどこにいるのか分からない多様体です。

滑らかな部分多様体が与えられたとき、任意のにおいて測地線がに完全に含まれる場合と同値である。このような多様体では、より大きな多様体上のアフィン接続は部分多様体上のアフィン接続であるため、部分多様体は自然にアフィン多様体となる。 $N\subset M$ $x\in N,\;v\in T_{x}N$ $M$ $(x,v)$ $N$

具体的には、点とを移動させる方向が与えられている場合、をの部分空間であるかのように測地線を用いてに沿って移動させます。移動先はの部分空間になります。はにおいて完全に測地線であるため、の移動先はに等しくなります。 $x\in N$ $v\in T_{x}N$ $T_{x}N$ $T_{x}M$ $v\in T_{x}M$ $\gamma (t)$ $T_{x}N$ $T_{\gamma (t)}M$ $N$ $M$ $T_{x}N$ $T_{\gamma (t)}N$

没入感

一般に、微分可能多様体浸漬は完全に測地線的ではない。つまり、から始まるの測地線はを直ちに離れる可能性がある。リーマンの場合、第二の基本形式がの測地線を内の最も近い曲線に曲げる。アフィンの場合、同様にアフィン基本形式を定義できるが、もはや唯一の自然な選択は存在しない。 $f:N\to M$ $M$ $f(N)$ $f(N)$ $M$ $f(N)$

がアフィン多様体であると仮定する。任意のにおいて、となるようなものを選び、の選択はが変化するにつれて滑らかに変化する。部分空間は、はめ込みに対する横断方向の選択として解釈できる。リーマン幾何学とは異なり、垂直性が定義されていないため、自然な選択は存在しない。 $(N,\nabla ),(M,\nabla ')$ $x\in N$ $V_{x}$ $T_{f(x)}M=f^{*}(T_{x}N)\oplus V_{x}$ $V_{x}$ $x\in N$ $V_{x}$

アフィン基本形式は、上の2 つのベクトル場を取り、内のベクトル場を生成する多重線型写像であり、となります。言葉で言えば、上のアフィン変換は、でのアフィン変換に加えて、横方向の補正を行うことで同様に実行できることを意味します。 $\alpha$ $X,Y$ $N$ $V$ $\nabla '_{X}f_{*}(Y)=f_{*}(\nabla _{X}Y)+\alpha (X,Y)$ $(N,\nabla )$ $(M,\nabla ')$

そのようなアフィン基本形式が存在する場合にのみ、は アフィン浸漬であると言えます。 $f:N\to M$

アフィン浸漬は、そのアフィン基本形式がゼロである場合に限り、完全に測地線的です。

座標

局所座標チャートが与えられると、接束を張るベクトル場の集合が生成されます。クリストッフェル記号はリーマン幾何学と同様に定義されます。リーマン幾何学では、ある点における法線座標により、レヴィ・チヴィタ接続のクリストッフェル記号はその特定の点で消滅します。これは、測地線を用いて指数写像を介して構築されます。この構築はアフィン接続に対しても有効です。このように、はであるため、「局所的にと同値」と見なすことができます。 $(x^{1},\dots ,x^{n}):M\supset U\to \mathbb {R} ^{n}$ $\partial _{1},\dots ,\partial _{n}$ $\nabla _{\partial _{i}}\partial _{j}=\Gamma _{ij}^{k}\partial _{k}$ $p\in M$ $\exp _{p}:T_{p}M\supset U\to M$ $M$ $\mathbb {A} ^{n}$ $\mathbb {A} ^{n}\cong T_{p}M$

この構成には捩れがゼロであることが必要である。なぜなら、正規座標が存在するためには、捩れがゼロでなければならないからである。これが、アフィン幾何学においてアフィン接続が捩れがないと仮定される理由の一つである。

座標を使用する代わりに、ビエルバイン形式を使用することもできます。

曲率

アフィン幾何学では、リーマン幾何学と同様に、曲率はアフィン幾何学のすべての局所的特徴を符号化します。具体的には、曲率テンソルと呼ばれる(1, 3)-テンソルがあり、同様に定義されます。同様に、テンソルを縮約することで得られるリッチ曲率テンソルと呼ばれる(0, 2)-テンソルがあります。ただし、リーマン幾何学とは異なり、リッチ曲率テンソルは非対称になる可能性があり、その結果、対称部分と反対称部分に分割されます。 $R(X,Y):=\nabla _{X}\nabla _{Y}-\nabla _{Y}\nabla _{X}-\nabla _{[X,Y]}$ $\operatorname {Ric} (X,Y):=\operatorname {Tr} (Z\mapsto R(Z,X)Y)$

アフィン多様体は、その曲率テンソルがゼロであるときのみ平坦である。リッチ平坦についても同様である。

$\operatorname {Ric}$ 平行移動に対して不変な体積形式が存在する場合のみ、開部分集合上で対称である。 $U\subset M$ $U$

どちらかの端でとなるようなアフィンパラメータ化された測地線がある場合、その測地線をその端に沿ってさらに延長する方法はなく、したがって本質的に不完全です（偶然にとなるのではなく）。 $\gamma :(t_{0},t_{1})\to M$ $\operatorname {Ric} ({\dot {\gamma }},{\dot {\gamma }})\to \pm \infty$

声明:

の場合、は局所的に対称です。 $\nabla R=0$ $(M,\nabla )$
がフルランクの場合、は擬リーマン形式と解釈でき、擬リーマン多様体を作成しますが、そのレヴィ・チヴィタ接続はではない可能性があります。 $\operatorname {Ric}$ $\operatorname {Ric}$ $(M,\operatorname {Ric} )$ $\nabla$
とがフルランクの場合、のレヴィ・チヴィタ接続はである。したがって、この場合、アフィン多様体は標準的には局所対称擬リーマン多様体である。 $\nabla R=0$ $\operatorname {Ric}$ $(M,\operatorname {Ric} )$ $\nabla$
$(M,\nabla )$ が局所対称であるためには、各点において測地線対称性がアフィン微分同相写像となる必要がある。測地線対称性は点の鏡映写を一般化したものであることに注意されたい。 $x$ $y\mapsto \exp _{x}(-\exp _{x}^{-1}(y))$

より一般的には、アフィン多様体が計量化可能であるのは、がに対するレヴィ・チヴィタ接続となるような擬リーマン形式をに課すことができる場合のみです。 $(M,\nabla )$ $g$ $M$ $\nabla$ $g$

ブラシュケ計量に関する微妙な点に注意する必要がある。上の任意の滑らかな有向超曲面に対して、ブラシュケ計量を用いて上の曲線の等アフィン弧長を定義することができ、それによりはリーマン多様体となる。しかし、ブラシュケ計量に対するレヴィ・チヴィタ接続は、必ずしもブラシュケ接続とは限らない。実際、曲面が厳密に凸面であっても二次曲面ではない場合は、これらは同じ接続ではない。 $M\subset \mathbb {R} ^{n}$ $M$ $M$

アフィン曲面

2次元の場合、それはアフィン曲面です。アフィン曲面には特別な性質があります。 $M$

ならば、は対称である。前の節の記述とは異なり、これはがフルランクであるという仮定を必要としないため、擬リーマン多様体ではない可能性がある。 $\nabla R=0$ $\operatorname {Ric}$ $\operatorname {Ric}$ $(M,\operatorname {Ric} )$

リーマン面に関しては、アフィン面が平坦であるためには、それがリッチ平坦である必要があります。

問題

アフィン微分幾何学におけるいくつかの基本的な問題は次のとおりです。

アフィン多様体が計量化可能かどうか
アフィン多様体が別のアフィン多様体に浸ることができるかどうか。
アフィン多様体が測地的に完備であるかどうか;
アフィン球の分類;
アフィン最大曲面の分類;
特に代数幾何学との相互作用におけるグローバル構造。
等

参照

参考文献

^ ^a ^b Su, Buchin (1983),アフィン微分幾何学, Harwood Academic, ISBN 0-677-31060-9
^サイモン、ウド、シュウェンク＝シェルシュミット、アンジェラ、ヴィーゼル、ヘルムート (1991).超曲面のアフィン微分幾何学入門. 講義ノート. 東京: 理科大学. ISBN 978-3-7983-1529-7。
^ Davis, D. (2006)、「 R ⁿにおける曲線の一般的なアフィン微分幾何学」、 Proc. Royal Soc. Edinburgh、136A、1195−1205。
^ ^a ^b ^c ^d ^e ^f野水功; 佐々木毅 (1994) 『アフィン微分幾何学：アフィン浸漬の幾何学』ケンブリッジ大学出版局、ISBN 0-521-44177-3
^ ^a ^bカルヴィーニョ＝ルサオ、エステバン;バスケス＝ロレンソ、ラモン。ガルシア＝リオ、エドゥアルド。ギルキー、ピーター。 Park, JeongH Hyun (2019)、「An Introduction to Affine Geometry」、Aspects of Differential Geometry IV、Cham: Springer International Publishing、pp. 1–42、doi : 10.1007/978-3-031-02416-0_1、ISBN 978-3-031-01288-4{{citation}}: CS1 maint: work parameter with ISBN (link)

[Su-1] Su, Buchin (1983),アフィン微分幾何学, Harwood Academic, ISBN 0-677-31060-9

[2] サイモン、ウド、シュウェンク＝シェルシュミット、アンジェラ、ヴィーゼル、ヘルムート (1991).超曲面のアフィン微分幾何学入門. 講義ノート. 東京: 理科大学. ISBN 978-3-7983-1529-7。

[Davis-3] Davis, D. (2006)、「 R ⁿにおける曲線の一般的なアフィン微分幾何学」、 Proc. Royal Soc. Edinburgh、136A、1195−1205。

[Nomizu-4] 野水功; 佐々木毅 (1994) 『アフィン微分幾何学：アフィン浸漬の幾何学』ケンブリッジ大学出版局、ISBN 0-521-44177-3

[:0-5] カルヴィーニョ＝ルサオ、エステバン;バスケス＝ロレンソ、ラモン。ガルシア＝リオ、エドゥアルド。ギルキー、ピーター。 Park, JeongH Hyun (2019)、「An Introduction to Affine Geometry」、Aspects of Differential Geometry IV、Cham: Springer International Publishing、pp. 1–42、doi : 10.1007/978-3-031-02416-0_1、ISBN 978-3-031-01288-4{{citation}}: CS1 maint: work parameter with ISBN (link)

[ 1 ]

[ 2 ]に基づいています。

[

[ 4 ]

[ 5 ]